Геометрия пространства в творчестве М. К. Эшера

Биография
Голландский художник Мориц Корнелиус Эшер, родившийся в 1898 году в Нидерландах, создал уникальные и очаровательные работы, в которых использован или показан широкий круг математических идей.
Автопортрет

Эшер родился в семье инженера. С детства он проявлял способности к рисованию, и его отдали учиться в школу архитектуры и декоративных искусств. Закончив школу, он уезжает путешествовать по Европе.

Он долгое время пробыл в Италии. Но проблемы со здоровьем вынуждают его вернутся на родину, где он и создаёт свои первые известные работы.
Водопад

Популярность пришла к Эшеру в 1950-ых годах. Его интервью стали печатать в популярных журналах, благодаря которым Эшер получил всемирно известную популярность. Его картины покупали музеи и университеты.
Отражение

Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это ещё более интересно тем, что сам Эшер не имел специального математического образования.
Геометрические тела

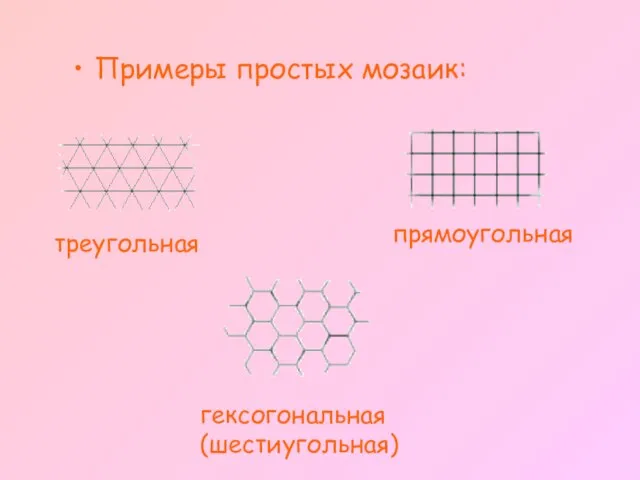
Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники.
Мозаики

Примеры простых мозаик:
треугольная
прямоугольная
гексогональная
(шестиугольная)

В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь, ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.
Мориц Корнелиус Эшер

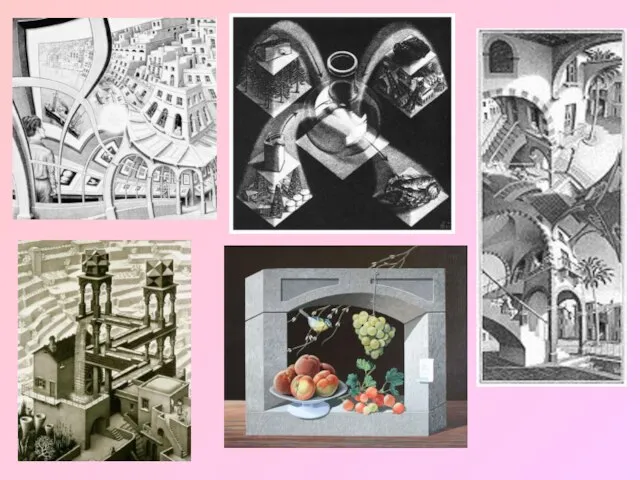
Он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шести направленную симметрию.

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во многих его работах многогранники являются главной фигурой, и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
Многогранники

Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона.

Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду.

Класс фигур, которые достаточно часто встречаются в работах Эшера - это закрученные спирали.
Здесь мы привели основные виды спиралей, использованных Эшером в своих работах. Различные их модификации можно обнаружить и на многих других литографиях художника.
Спирали

Использование Эшером различных математических фигур и законов не ограничивается лишь вышеприведенными примерами. Внимательно изучая его картины, можно обнаружить и другие геометрические тела или визуальную интерпретацию математических законов

Форма пространства
Среди наиболее важных работ Эшера с математической точки зрения выделяются картины, оперирующие с природой самого пространства.
Литография "Три пересекающиеся плоскости" - хороший пример для начала обзора таких картин.

Кроме особенностей евклидовой и неевклидовой геометрий Эшера интересовали визуальные аспекты топологии. Топология изучает свойства тел и поверхностей пространства, которые не изменяются при деформации. Единственное, к чему не должна приводить деформация - это к разрыву.

Топологам приходится изображать множество странных объектов. Одним из наиболее известных является «лента Мебиуса», которая встречается во многих работах Эшера.

Сделать лист Мебиуса очень просто. Надо взять полоску бумаги, изогнуть ее, и склеить противоположные края ленты клеем.

Под "логикой" пространства мы понимаем те отношения между физическими объектами, которые обычны для реального мира, и при нарушении которых возникают визуальные парадоксы, называемые еще оптическими иллюзиями.
Логика пространства

Еще один из аспектов логики пространства - перспектива. На рисунках, в которых присутствует эффект перспективы, выделяют так называемые точки исчезновения, которые сообщают глазу человека о бесконечности пространства.

Третий тип картин с нарушенной логикой пространства - это "невозможные фигуры". Парадокс невозможных фигур основан на том, что наш мозг всегда пытается представить нарисованные на бумаге двухмерные рисунки как трехмерные. Эшер создал много работ, в которых обратился к этой аномалии.

Наиболее полное исследование этого вопроса освещено в книге Дугласа Хофстадтера "Гёдель, Эшер, Бах: Бесконечная золотая нить" выпущенной в 1980 году и награжденной Пулитцеровской премией.
Самовоспроизведение и информация

Одна из самых известных литографий Эшера, иллюстрирующая самовоспроизведение, это «Рисующие руки»

Углубляясь в изучение самовоспроизведения, можно его обнаружить в отражении и пересечении отражений реального мира. Такое пересечение встречается во многих картинах Эшера. Мы рассмотрим лишь один пример - литографию "Три сферы"