Графическое решение квадратных уравнений

Алгоритм решения уравнения вида f(x)=g(x) графическим способом
Рассмотрим две функции y=f (x) и y=g (x)
Построим график функции y=f (x)
Построим график функции y=g (x)
Найдём координаты точек пересечения построенных графиков; абсциссы этих точек – корни уравнения f(x)=g(x)

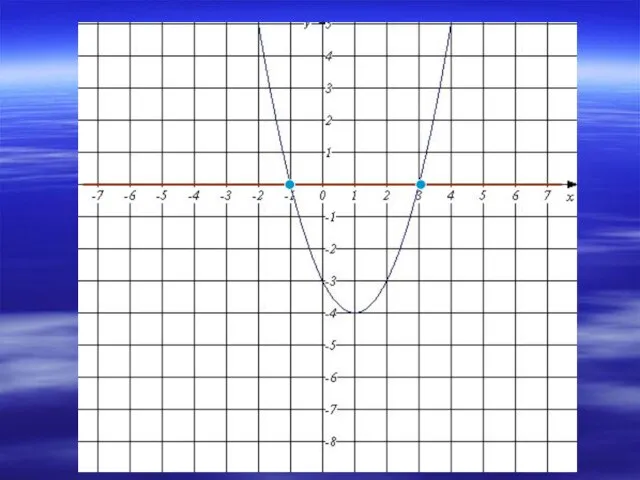
Решить уравнение: х2-2х-3=0
1. Рассмотрим функции у=х2-2х-3 и у=0
2. Построим график функции у=х2-2х-3 – функция квадратичная, графиком является парабола, ветви которой направлены вверх.
а) Найдём координаты вершины параболы А(х0;у0): а=1; в=-2
Х0=
У0=12-2∙1-3=-4
б) Осью симметрии является прямая х=1
3. Построим график функции у=0. Графиком данной функции является ось х.
4.Найдём координаты точек пересечения графиков функций:(-1;0) и (3;0). Значит решением уравнения являются их абсциссы.
Ответ: -1;3.

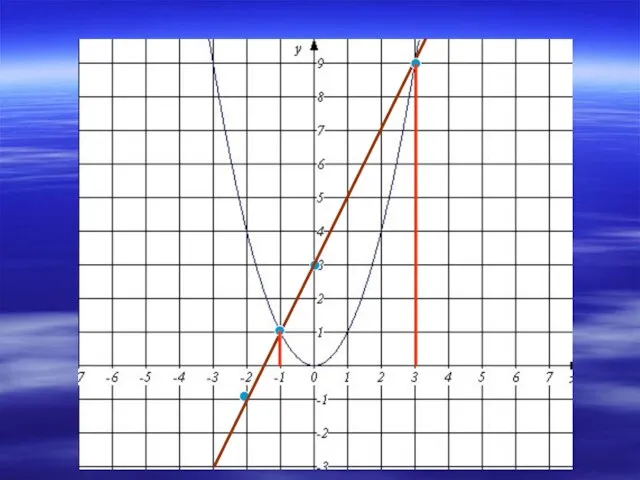
Решить уравнение: х2-2х-3=0
Второй способ:
Преобразуем уравнение х2-2х-3=0 к виду х2=2х+3
1. Рассмотрим функции у=х2 и у=2х+3
2. Построим график функции у=х2
3. Построим график функции у=2х+3 – функция линейная, графиком является прямая
4. Найдём координаты точек пересечения:
(-1;1) и (3;9). Значит решением данного уравнения являются абсциссы точек пересечения.
Ответ: -1; 3.

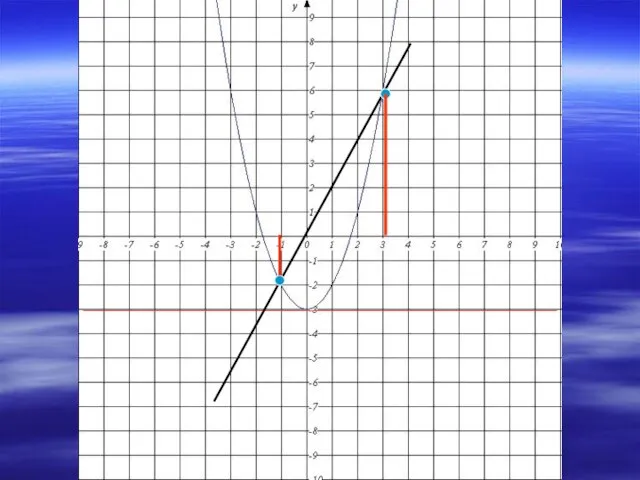
Решить уравнение: х2-2х-3=0
Третий способ:
Преобразуем уравнение к виду х2-3 = 2х.
1. Рассмотрим функции у = х2-3 и у = 2х.
2. Построим график функции у = х2-3
а) Данная функция получена из функции у = х2
б) Построим график функции у = х2:
в) Переместим начало системы координат на 3 единичных отрезка вниз вдоль оси у.
3. Построим график функции у = 2х – функция прямая пропорциональность, графиком является прямая, проходящая через начало координат.
4. Найдём координаты точек пересечения:
(-1;-2) и (3;6). Решением уравнения являются их абсциссы.
Ответ: -1; 3.