Содержание
- 2. Анализ путей. Одним из современных методов моделирования является анализ путей. Сам метод был предложен еще в
- 3. Путевые диаграммы Райта Кружки и квадраты соединяются между собой стрелками, которые обозначают предполагаемые связи между переменными.
- 4. Связь регрессии, дисперсии и путевых диаграмм Райта
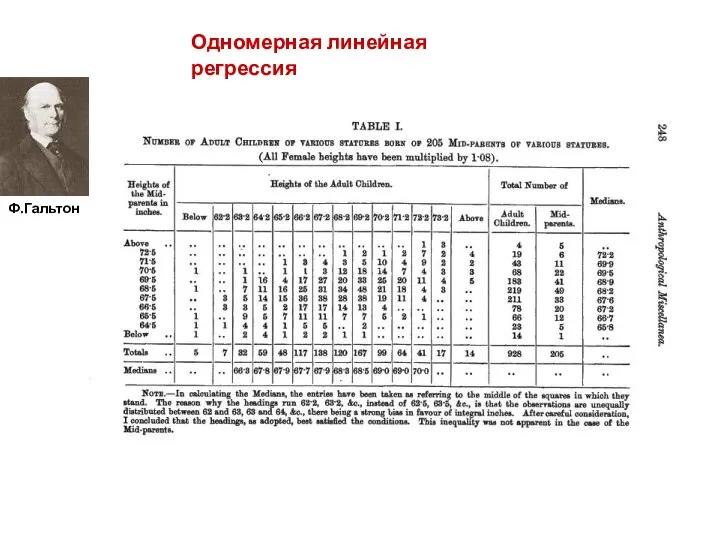
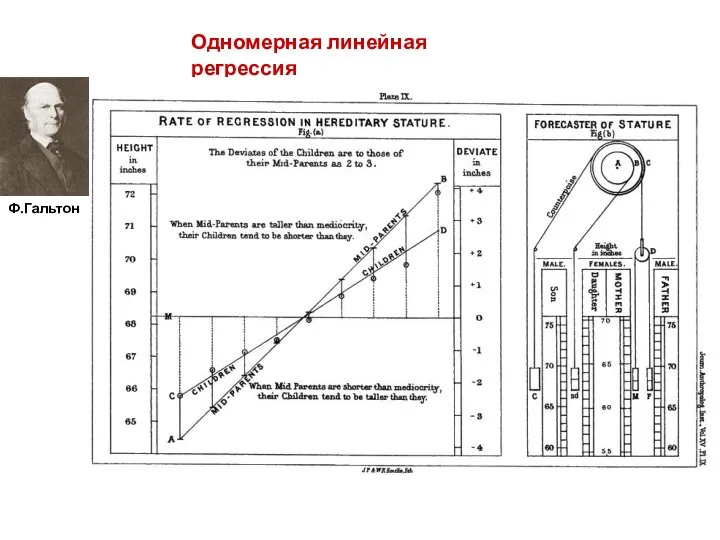
- 5. Одномерная линейная регрессия Ф.Гальтон
- 6. Одномерная линейная регрессия Ф.Гальтон
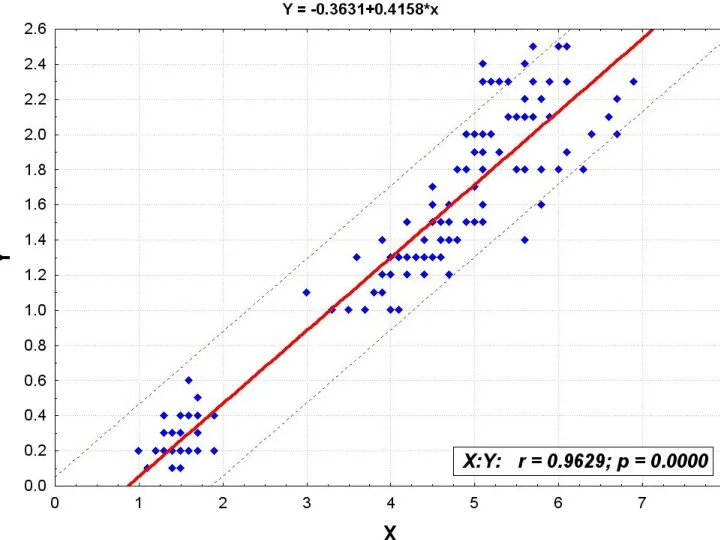
- 7. Уравнение линейной регресии. Метод наименьших квадратов
- 9. Будем считать, что обе переменные центрированы и нормированы. Уравнение ỹ=ax+b – это оценка зависимости у от
- 10. Связь регрессии и дисперсии. Путь X --- Y ∑ yi2/N= σy2= 1; ∑ xi2/N= σx2= 1;
- 11. Связь регрессии и дисперсии. Путь X --- Y Но можно рассмотреть регрессию Х наY . Получим,
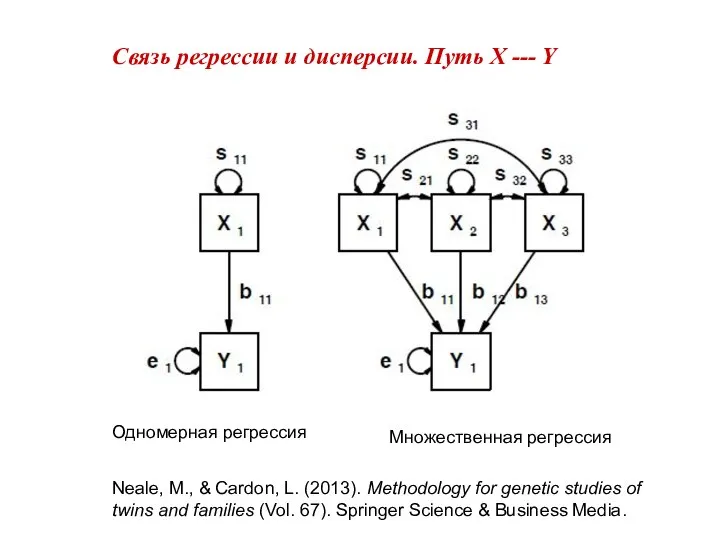
- 12. Связь регрессии и дисперсии. Путь X --- Y Одномерная регрессия Множественная регрессия Neale, M., & Cardon,
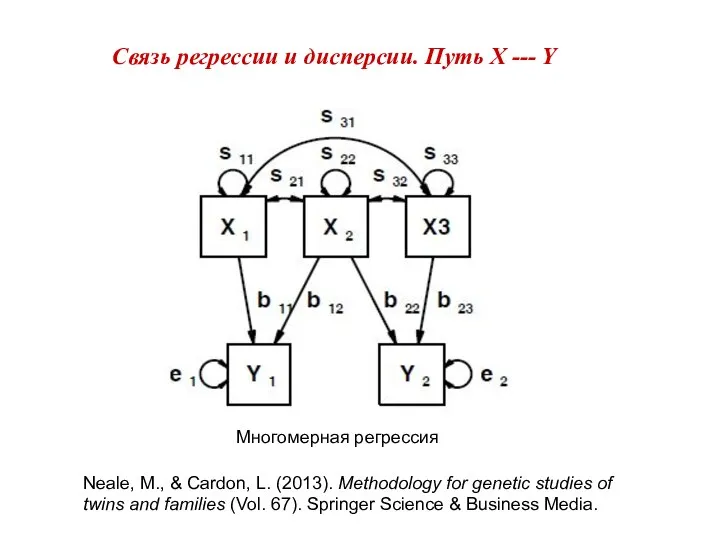
- 13. Связь регрессии и дисперсии. Путь X --- Y Многомерная регрессия Neale, M., & Cardon, L. (2013).
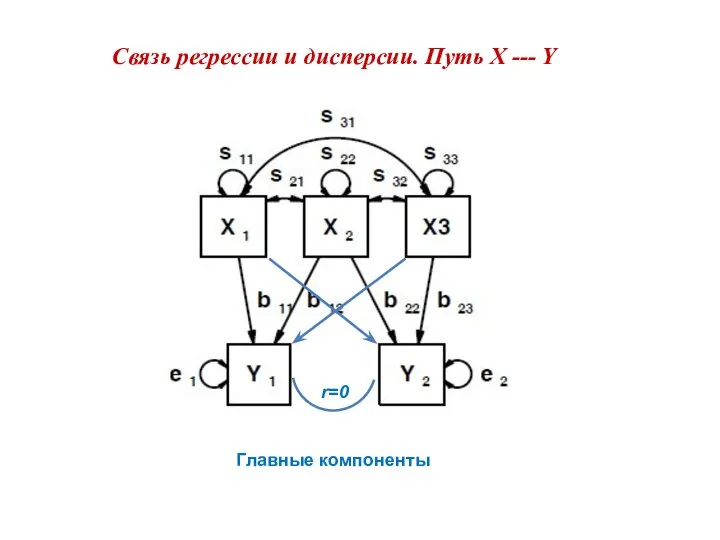
- 14. Связь регрессии и дисперсии. Путь X --- Y Главные компоненты r=0
- 15. Коэффициент наследуемости (гетерогенные родители и потомки) Lush. I. L. 1937. Animal Breeding Plans. Collegiate Press, Inc.,
- 16. Нас интересует прежде всего аддитивный эффект. Именно он отвечает за успешность отбора. Коэффициент наследуемости (гетерогенные родители
- 17. Коэффициент наследуемости (гетерогенные родители и потомки) в широком смысле: в узком смысле: То есть, коэффициент наследуемости
- 18. Коэффициент наследуемости (гетерогенные родители и потомки) G P h В единицах стандартного отклонения: Здесь ситуация не
- 19. Коэффициент наследуемости (гетерогенные родители и потомки) Lush. I. L. 1937. Animal Breeding Plans. Collegiate Press, Inc.,
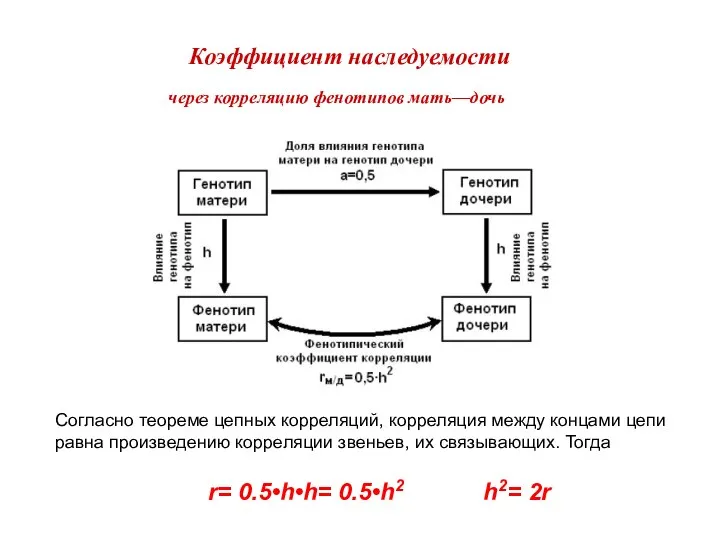
- 20. Коэффициент наследуемости через корреляцию фенотипов мать—дочь Согласно теореме цепных корреляций, корреляция между концами цепи равна произведению
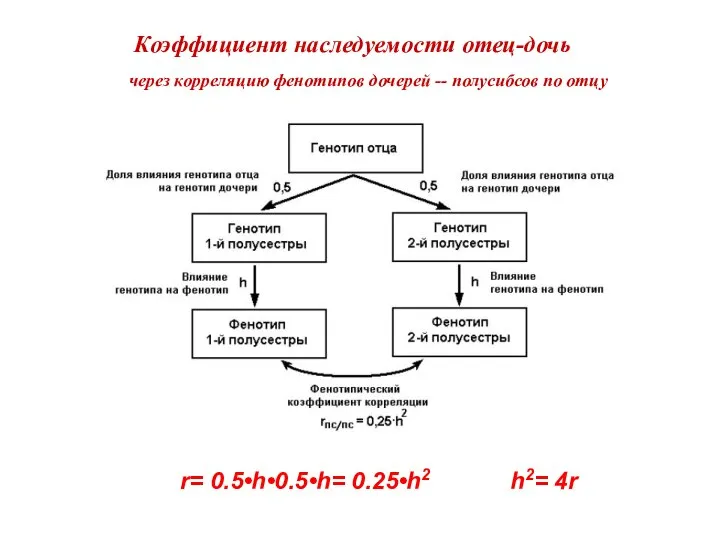
- 21. Коэффициент наследуемости отец-дочь через корреляцию фенотипов дочерей -- полусибсов по отцу Сходство родственников, принадлежащих к разным
- 22. Коэффициент наследуемости отец-дочь через корреляцию фенотипов дочерей -- полусибсов по отцу r= 0.5•h•0.5•h= 0.25•h2 h2= 4r
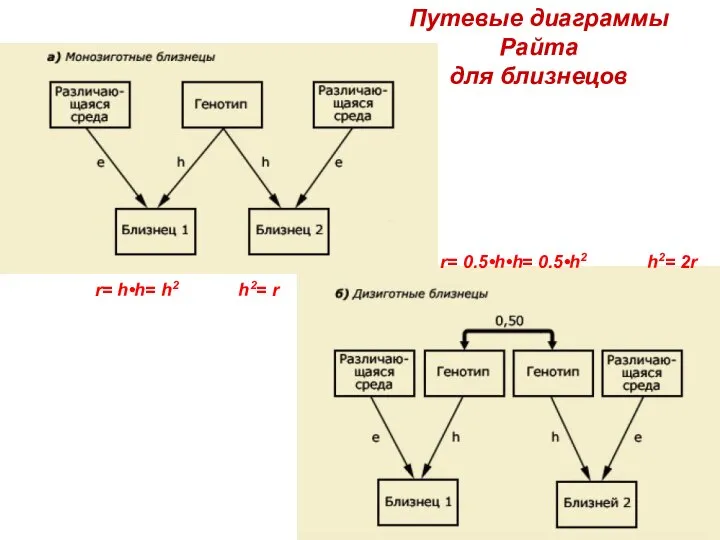
- 23. Путевые диаграммы Райта для близнецов r= 0.5•h•h= 0.5•h2 h2= 2r r= h•h= h2 h2= r
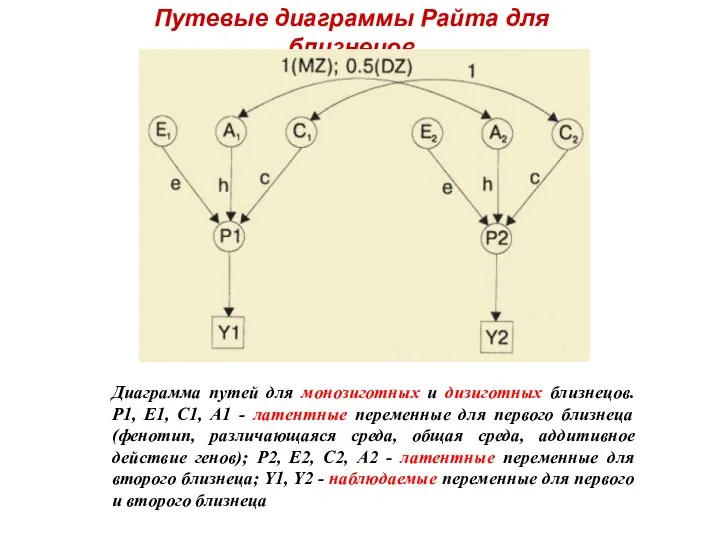
- 24. Путевые диаграммы Райта для близнецов Диаграмма путей для монозиготных и дизиготных близнецов. P1, E1, C1, A1
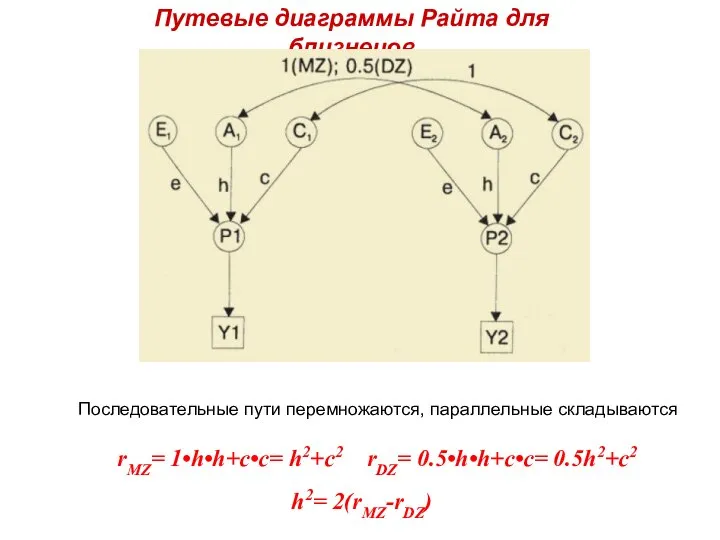
- 25. Путевые диаграммы Райта для близнецов rMZ= 1•h•h+c•c= h2+c2 rDZ= 0.5•h•h+c•c= 0.5h2+c2 h2= 2(rMZ-rDZ) Последовательные пути перемножаются,
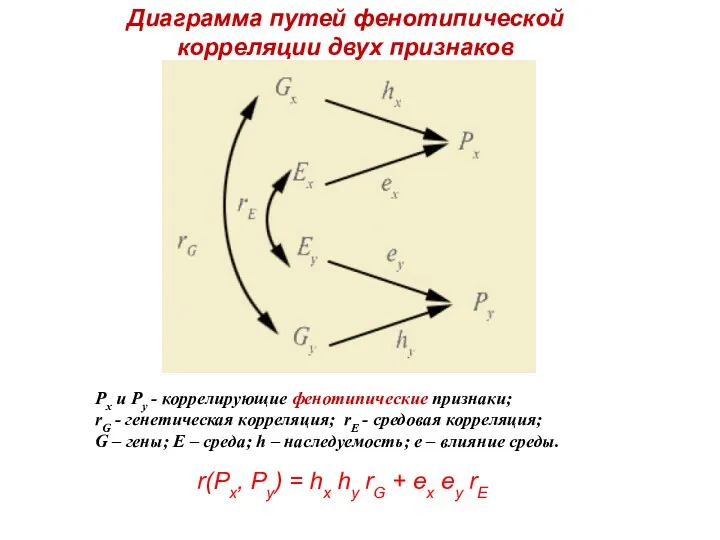
- 26. Рх и Ру - коррелирующие фенотипические признаки; rG - генетическая корреляция; rE - средовая корреляция; G
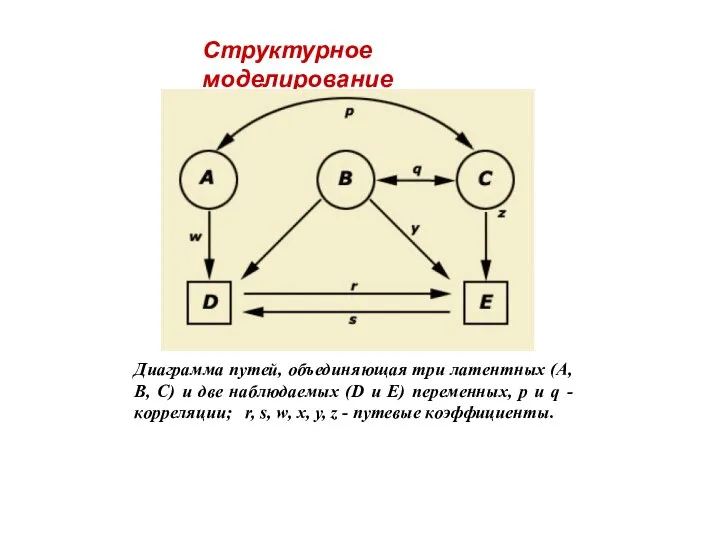
- 27. Структурное моделирование применяется в эконометрике и представляет собой один из наиболее сложных современных методов. По существу,
- 28. Диаграмма путей, объединяющая три латентных (А, В, С) и две наблюдаемых (D и Е) переменных, р
- 29. Спасибо за внимание!
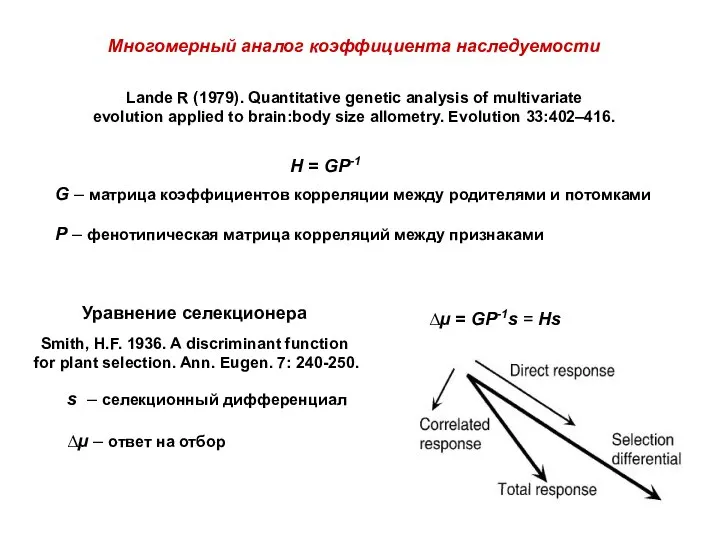
- 30. H = GP-1 Многомерный аналог коэффициента наследуемости Lande R (1979). Quantitative genetic analysis of multivariate evolution
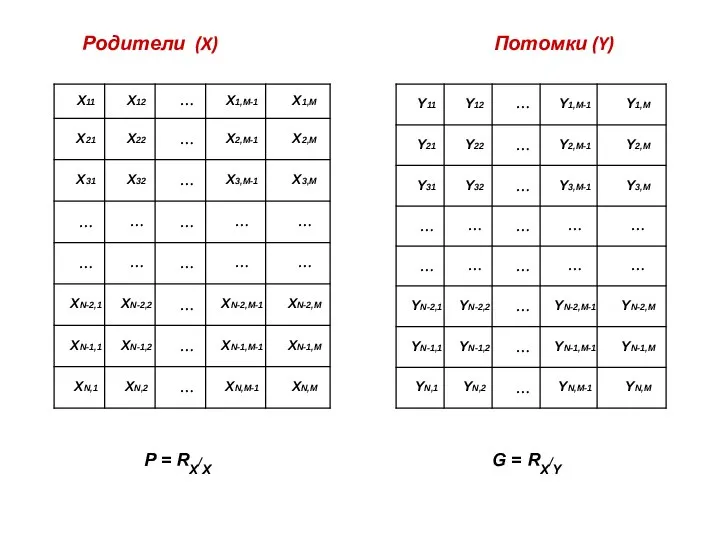
- 31. Родители (X) Потомки (Y) P = RX/X G = RX/Y
- 32. Поиск осей с максимальной наследуемостью (в узком смысле) Ott J, Rabinowitz D (1999). A principal-components approach
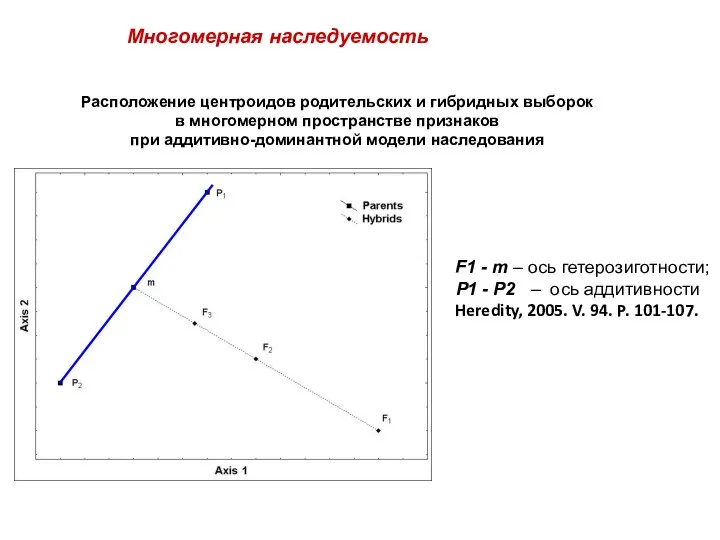
- 34. Расположение центроидов родительских и гибридных выборок в многомерном пространстве признаков при аддитивно-доминантной модели наследования F1 -
- 35. F1 - F# – ось гетерозиготности H P1 - P2 – ось аддитивности A m -
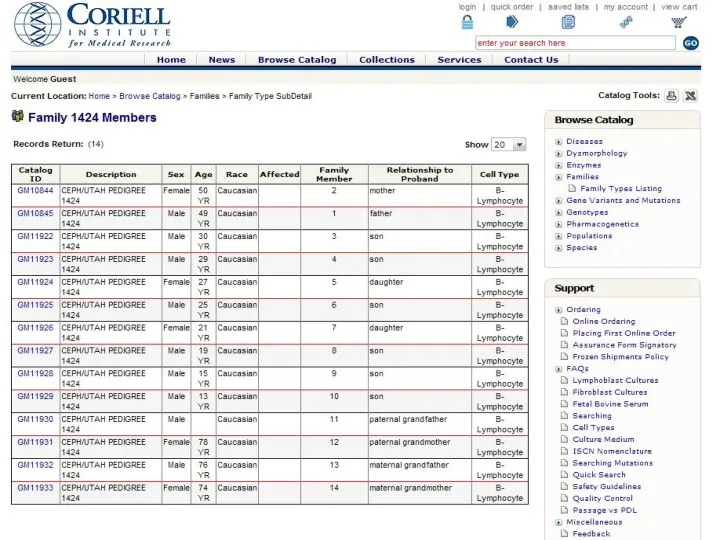
- 37. Материал
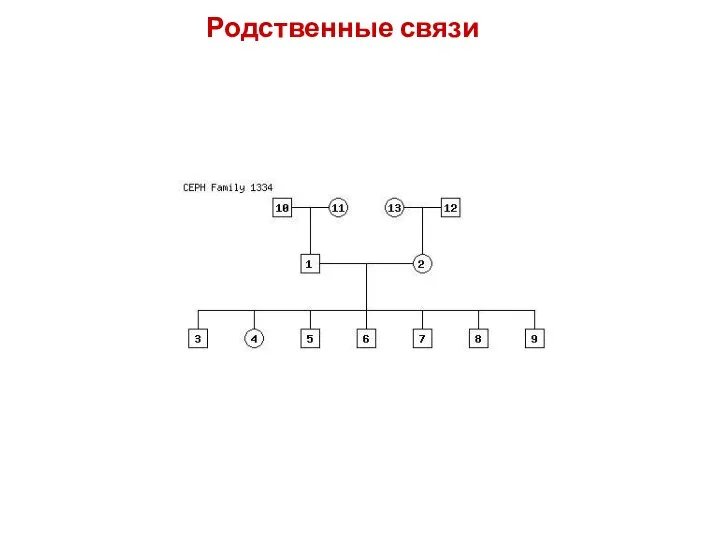
- 39. Родственные связи
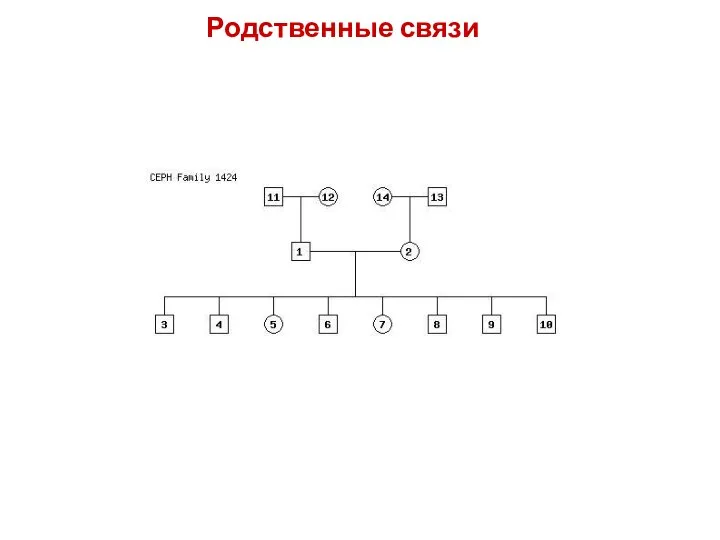
- 40. Родственные связи
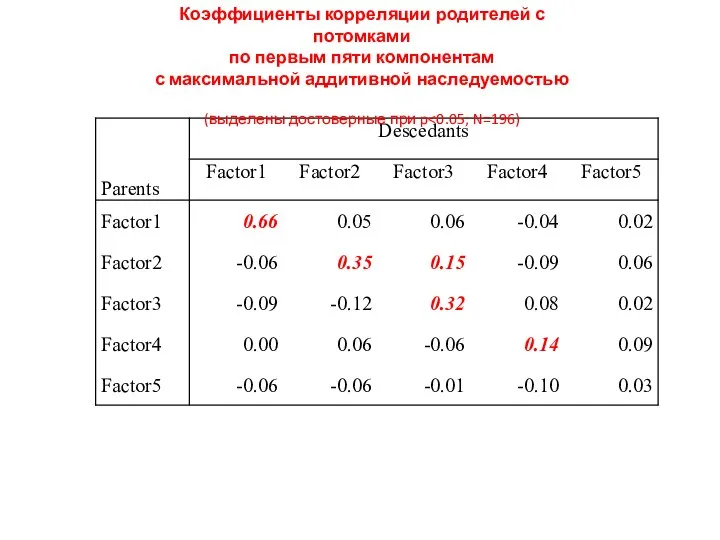
- 41. Коэффициенты корреляции родителей с потомками по первым пяти компонентам с максимальной аддитивной наследуемостью (выделены достоверные при
- 42. Коэффициент наследуемости через корреляции “родитель-потомок”: один родитель - потомок (в случае отсутствия ассортативности) один родитель -
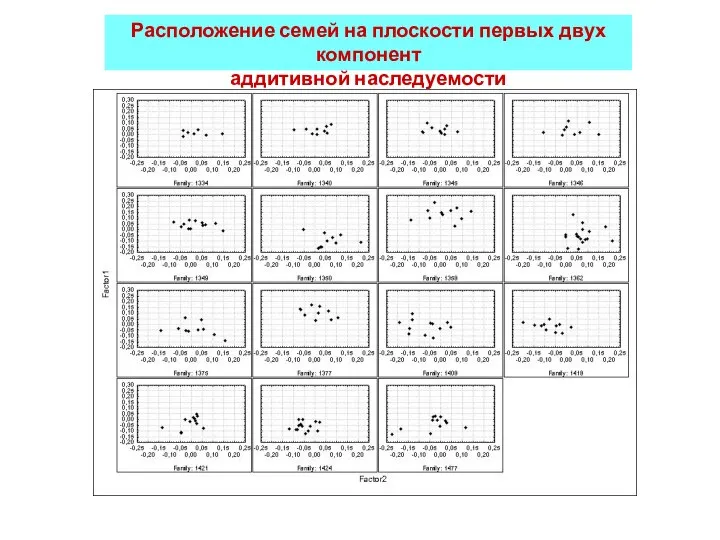
- 43. Расположение семей на плоскости первых двух компонент аддитивной наследуемости
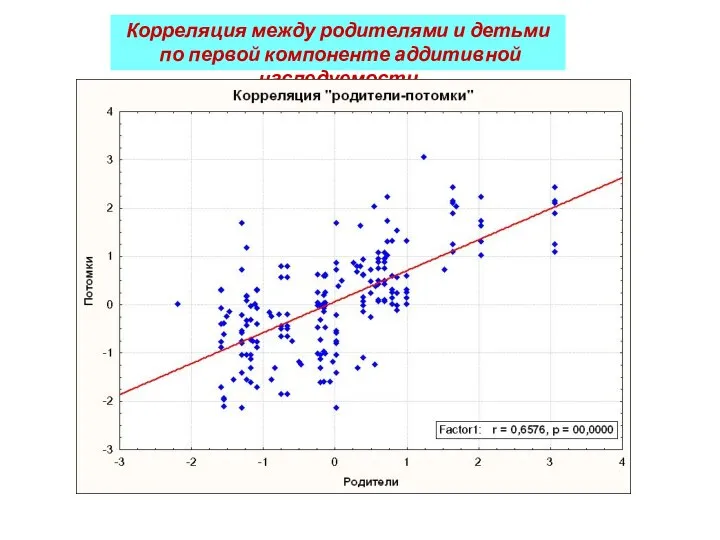
- 44. Корреляция между родителями и детьми по первой компоненте аддитивной наследуемости
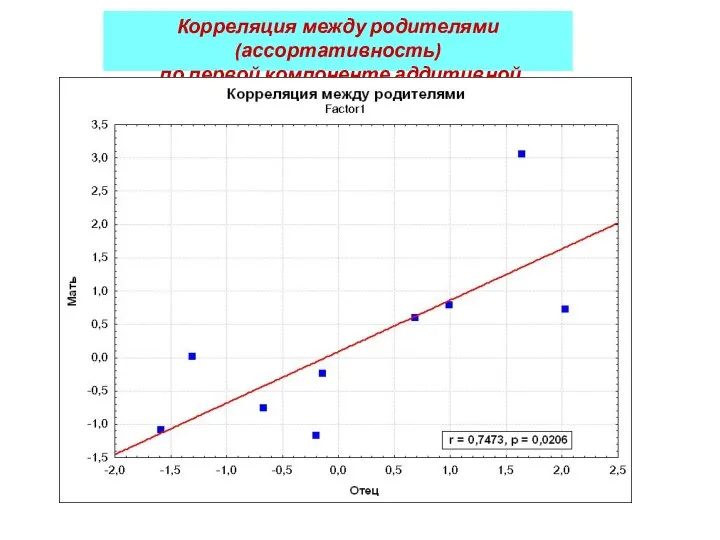
- 45. Корреляция между родителями (ассортативность) по первой компоненте аддитивной наследуемости
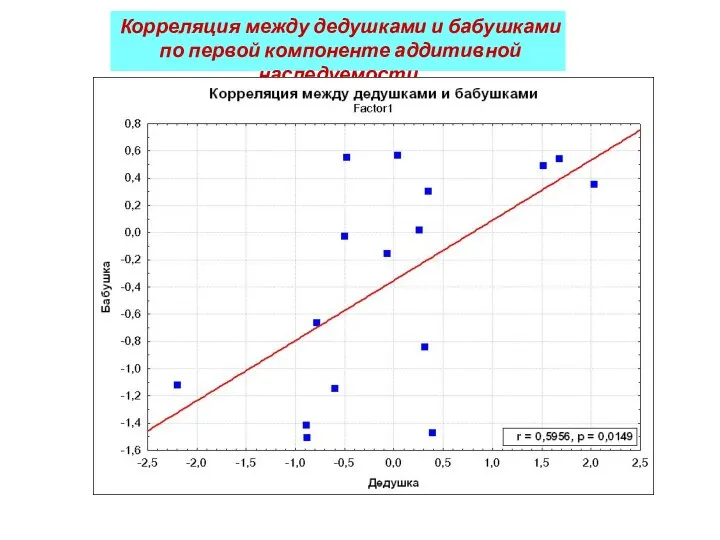
- 46. Корреляция между дедушками и бабушками по первой компоненте аддитивной наследуемости
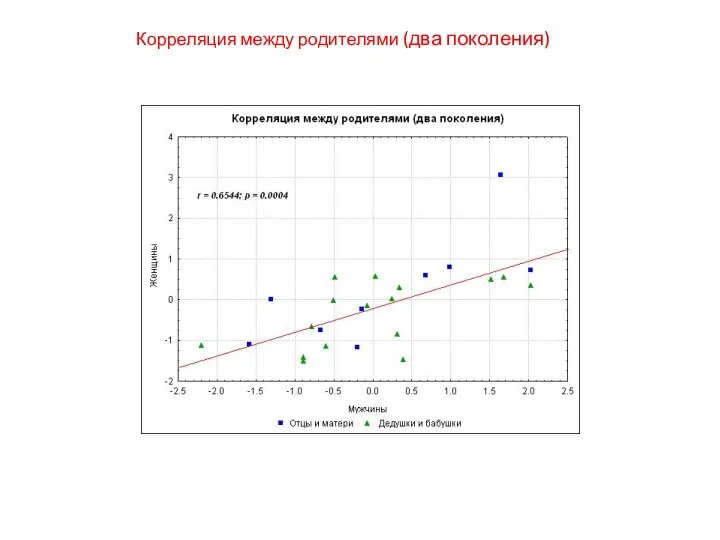
- 47. Корреляция между родителями (два поколения)
- 49. Скачать презентацию




















 Организационная структура страховой компании
Организационная структура страховой компании STUDYING PHENOMENA AND PROCESSES
STUDYING PHENOMENA AND PROCESSES  Reported / Indirect Speech.(Косвенная речь.)
Reported / Indirect Speech.(Косвенная речь.) Презентация на тему Дробные выражения 6 класс
Презентация на тему Дробные выражения 6 класс Подготовка к сочинению С2.1 (ГИА 2012, 9 класс) Автор: Морозова Алла Станиславовна, учитель русского языка и литературы
Подготовка к сочинению С2.1 (ГИА 2012, 9 класс) Автор: Морозова Алла Станиславовна, учитель русского языка и литературы Система «Регистр АГ» это новый методологический подход к оценке качества медицинской помощи больным артериальной гипертонией в
Система «Регистр АГ» это новый методологический подход к оценке качества медицинской помощи больным артериальной гипертонией в Классный час для 6 класса. Тема: Выбор профессии в современном мире. - презентация
Классный час для 6 класса. Тема: Выбор профессии в современном мире. - презентация Мауриц Эшер, голландский художник- график. 6 класс
Мауриц Эшер, голландский художник- график. 6 класс Моря, озёра, реки
Моря, озёра, реки Финансовая стратегия бизнес-планирования
Финансовая стратегия бизнес-планирования Presentation 4
Presentation 4 Сибирская язва
Сибирская язва Снег в нашей жизни
Снег в нашей жизни Отчет по практике (по получению профессиональных умений и опыта профессиональной деятельности магистранта)
Отчет по практике (по получению профессиональных умений и опыта профессиональной деятельности магистранта) Организация работы по выявлению неформальной занятости и легализации трудовых отношений в республике САХА
Организация работы по выявлению неформальной занятости и легализации трудовых отношений в республике САХА Вес воздуха. Атмосферное давление 7 класс
Вес воздуха. Атмосферное давление 7 класс Учебный проект
Учебный проект Наглядное представление статистической
Наглядное представление статистической Викторина - юморина
Викторина - юморина Спам и способы борьбы с ним
Спам и способы борьбы с ним Проект - Про Воркаут в городе Королёв
Проект - Про Воркаут в городе Королёв Типичные ошибки при выполнении заданий ЕГЭ по химии
Типичные ошибки при выполнении заданий ЕГЭ по химии Банковская система
Банковская система Оценка качества и подтверждение соответствия требованиям технических нормативных правовых актов швейных изделий,
Оценка качества и подтверждение соответствия требованиям технических нормативных правовых актов швейных изделий, Расчет внутреннего водопровода и канализации 7 этажного здания, индивидуальной планировки, дворовая сеть канализации
Расчет внутреннего водопровода и канализации 7 этажного здания, индивидуальной планировки, дворовая сеть канализации Правовое регулирование страховых выплат и страховое мошенничество
Правовое регулирование страховых выплат и страховое мошенничество Образовательная система в странах Востока (Китай, Корея, Япония)
Образовательная система в странах Востока (Китай, Корея, Япония) Уголь
Уголь