Хэширование (hashing). Хэш-таблицы (Hash tables).

Хэширование–это преобразование входного массива данных определенного типа и произвольной длины
в выходную битовую строку фиксированной длины.
Такие преобразования также называются хеш-функциями или функциями свертки, а их результаты называют хэшем, хэш-кодом, хэш-таблицей или дайджестом сообщения (message digest).

Хеширование применяется для сравнения данных: если у двух массивов хеш-коды разные, массивы гарантированно различаются; если одинаковые — массивы, скорее всего, одинаковы.
В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов входного массива.

Существует множество массивов, дающих одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
Существует множество алгоритмов хеширования с различными характеристиками. Выбор той или иной хеш-функции определяется спецификой решаемой задачи.

Идея хеширования впервые была высказана Г.П. Ланом при создании внутреннего меморандума IBM в январе 1953 г. с предложением использовать для разрешения коллизий (ситуаций, когда разным ключам соответствует одно значение хеш-функции) метод цепочек.
Примерно в это же время другой сотрудник IBM, Жини Амдал, высказала идею использования открытой линейной адресации.

В открытой печати хеширование впервые было описано Арнольдом Думи (1956 год), указавшим, что в качестве хеш-адреса удобно использовать остаток от деления на простое число. А. Думи описывал метод цепочек для разрешения коллизий, но не говорил об открытой адресации.
Подход к хешированию, отличный от метода цепочек, был предложен А.П. Ершовым (1957 год), который разработал и описал метод линейной открытой адресации.

Хэш-таблица – это структура данных, реализующая интерфейс ассоциативного массива, то есть она позволяет хранить пары вида "ключ- значение" и выполнять три операции:
операцию добавления новой пары;
операцию поиска;
операцию удаления пары по ключу.
Хэш-таблица является массивом, формируемым в определенном порядке хэш-функцией.

С точки зрения практического применения, хорошей является такая хэш-функция, которая удовлетворяет следующим условиям:
функция должна быть простой с вычислительной точки зрения;
функция должна распределять ключи в хэш-таблице наиболее равномерно;
функция не должна отображать какую-либо связь между значениями ключей в связь между значениями адресов;
функция должна минимизировать число коллизий,то есть ситуаций, когда разным ключам соответствует одно значение хэш-функции (ключи в этом случае называются синонимами).

Если бы все данные были случайными, то хэш-функции были бы очень простые (например, несколько битов ключа).
Однако,на практике случайные данные встречаются достаточно редко, и приходится создавать функцию, которая зависит от всего ключа.
Если хэш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то хэширование эффективно разбивает множество ключей.
NB!Наихудший случай: все ключи хэшируются в один индекс.

При возникновении коллизий (разным ключам соответствует одно значение хэш-функции) необходимо найти новое место для хранения ключей, претендующих на одну и ту же ячейку хэш-таблицы.
Причем, если коллизии допускаются, то их количество необходимо минимизировать.
В некоторых специальных случаях удается избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую инъективную1 хэш-функцию, которая распределит их по ячейкам хэш-таблицы без коллизий. Хэш-таблицы, использующие подобные хэш-функции, не нуждаются в механизме разрешения коллизий, и называются хэш-таблицами с прямой адресацией.
1 - Организация связи «один к одному» между таблицами реляционной базы данных на основе первичных ключей.

Хэш-таблицы должны соответствовать следующим свойствам:
Выполнение операции в хэш-таблице начинается с вычисления хэш-функции от ключа. Получающееся хэш-значение является индексом в исходном массиве.
Количество хранимых элементов массива, деленное на число возможных значений хэш-функции, называется коэффициентом заполнения хэш-таблицы (load factor) и является важным параметром, от которого зависит среднее время выполнения операций.
Операции поиска, вставки и удаления должны выполняться в среднем за время O(1). Однако при такой оценке не учитываются возможные аппаратные затраты на перестройку индекса хэш-таблицы, связанную с увеличением значения размера массива и добавлением в хэш-таблицу новой пары.Механизм разрешения коллизий является важной составляющей любой хэш-таблицы.

Хэширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа.
Хэш-таблицы часто применяются в
базах данных,
языковых процессорах типа компиляторов и ассемблеров, где они повышают скорость обработки таблицы идентификаторов.
В качестве использования хэширования в повседневной жизни можно привести примеры:
распределение книг в библиотеке по тематическим каталогам,
упорядочивание в словарях по первым буквам слов,
шифрование специальностей в вузах и т.д.

Методы разрешения коллизий
Коллизии, когда разным ключам соответствует одно значение хэш-функции, осложняют использование хэш-таблиц, т.к. нарушают однозначность соответствия между хэш-кодами и данными.
Тем не менее, существуют способы преодоления возникающих сложностей:
метод цепочек (внешнее или открытое хэширование);
метод открытой адресации (закрытое хэширование).

Метод цепочек
Технология сцепления элементов состоит в том, что элементы множества, которым соответствует одно и то же хэш-значение, связываются в цепочку-список:
в позиции номер i хранится указатель на голову списка тех элементов, у которых хэш-значение ключа равно i;
если таких элементов в множестве нет, в позиции i записан NULL.

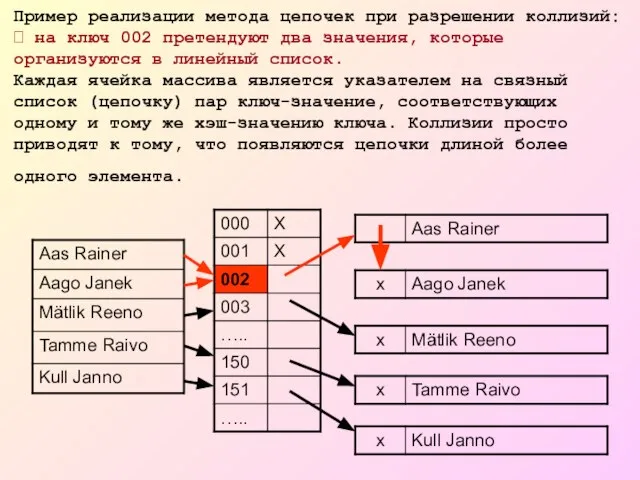
Пример реализации метода цепочек при разрешении коллизий: ? на ключ 002 претендуют два значения, которые организуются в линейный список.
Каждая ячейка массива является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хэш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.

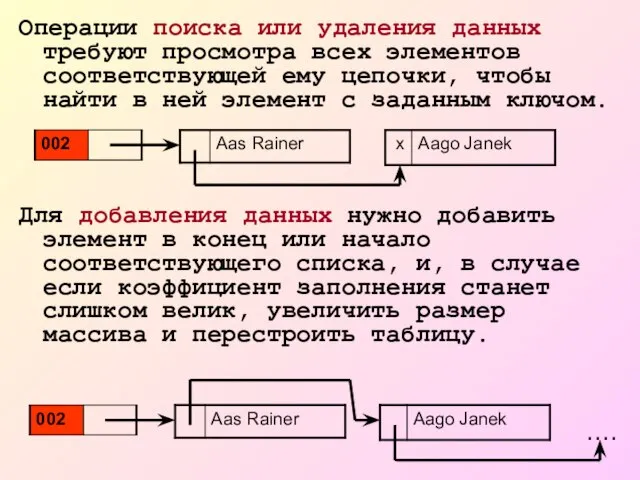
Операции поиска или удаления данных требуют просмотра всех элементов соответствующей ему цепочки, чтобы найти в ней элемент с заданным ключом.
Для добавления данных нужно добавить элемент в конец или начало соответствующего списка, и, в случае если коэффициент заполнения станет слишком велик, увеличить размер массива и перестроить таблицу.
....

При предположении, что каждый элемент может попасть в любую позицию таблицы с равной вероятностью и независимо от того, куда попал любой другой элемент, среднее время работы операции поиска элемента составляет O(1+k), где k – коэффициент заполнения таблицы.

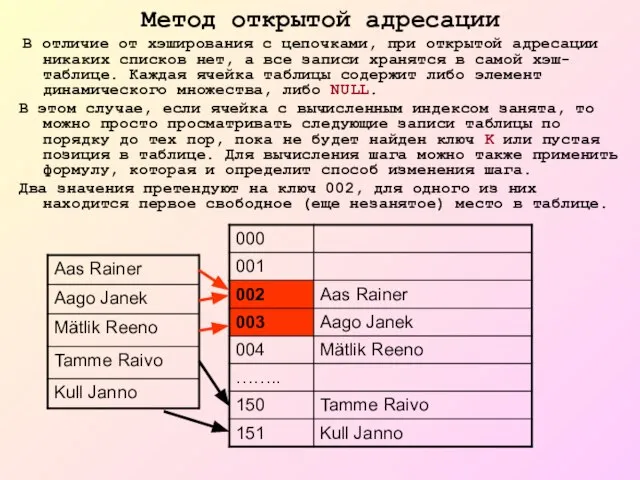
Метод открытой адресации
В отличие от хэширования с цепочками, при открытой адресации никаких списков нет, а все записи хранятся в самой хэш-таблице. Каждая ячейка таблицы содержит либо элемент динамического множества, либо NULL.
В этом случае, если ячейка с вычисленным индексом занята, то можно просто просматривать следующие записи таблицы по порядку до тех пор, пока не будет найден ключ K или пустая позиция в таблице. Для вычисления шага можно также применить формулу, которая и определит способ изменения шага.
Два значения претендуют на ключ 002, для одного из них находится первое свободное (еще незанятое) место в таблице.

При любом методе разрешения коллизий необходимо ограничить длину поиска элемента!!!!!!!!.
Если для поиска элемента необходимо более 3–4 сравнений, то эффективность использования такой хэш-таблицы пропадает и ее следует реструктуризировать (т.е. найти другую хэш-функцию), чтобы минимизировать количество сравнений для поиска элемента.
Для успешной работы алгоритмов поиска, последовательность проб должна быть такой, чтобы все ячейки хэш-таблицы оказались просмотренными ровно по одному разу.
Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят логический флаг для каждой ячейки, помечающий, удален ли элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хэш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удаленные ячейки занятыми, а процедуру добавления – чтобы она их считала свободными и сбрасывала значение флага при добавлении.

Алгоритмы хэширования
Существует несколько типов функций хеширования, каждая из которых имеет свои преимущества и недостатки и основана на представлении данных.

Таблица прямого доступа
Простейшей организацией таблицы, обеспечивающей идеально быстрый поиск, является таблица прямого доступа.
В такой таблице ключ является адресом записи в таблице или может быть преобразован в адрес, причем таким образом, что никакие два разных ключа не преобразуются в один и тот же адрес.
При создании таблицы выделяется память для хранения всей таблицы и заполняется пустыми записями. Затем записи вносятся в таблицу – каждая на свое место, определяемое ее ключом. При поиске ключ используется как адрес и по этому адресу выбирается запись. Если выбранная запись пустая, то записи с таким ключом вообще нет в таблице. Таблицы прямого доступа очень эффективны в использовании, но, к сожалению, область их применения весьма ограничена.

Пространство ключей - множество всех теоретически возможных значений ключей записи.
Пространство записей - множество тех ячеек памяти, которые выделяются для хранения таблицы.
ТАБЛИЦЫ ПРЯМОГО ДОСТУПА ПРИМЕНИМЫ ТОЛЬКО ДЛЯ ТАКИХ ЗАДАЧ, В КОТОРЫХ РАЗМЕР ПРОСТРАНСТВА ЗАПИСЕЙ МОЖЕТ БЫТЬ РАВЕН РАЗМЕРУ ПРОСТРАНСТВА КЛЮЧЕЙ.

В большинстве реальных задач размер пространства записей много меньше, чем пространства ключей.
Например, если в качестве ключа используется фамилия, то, даже ограничив длину ключа десятью символами кириллицы, получаем 3310 возможных значений ключей.
Даже, если ресурсы вычислительной системы и позволят выделить пространство записей такого размера, то значительная часть этого пространства будет заполнена пустыми записями, так как в каждом конкретном заполнении таблицы фактическое множество ключей не будет полностью покрывать пространство ключей.

В целях экономии памяти можно назначать размер пространства записей равным размеру фактического множества записей или превосходящим его незначительно.
В этом случае необходимо иметь некоторую функцию, обеспечивающую отображение точки из пространства ключей в точку в пространстве записей, то есть, преобразование ключа в адрес записи: a=h(k), где a – адрес, k – ключ.
Идеальной хэш-функцией является функция, которая для любых двух неодинаковых ключей дает неодинаковые адреса.

Метод остатков от деления
Простейшей хэш-функцией является деление по модулю числового значения ключа Key на размер пространства записи HashTableSize. Результат интерпретируется как адрес записи.
Однако операция деления по модулю обычно применяется как последний шаг в более сложных функциях хэширования, обеспечивая приведение результата к размеру пространства записей.

Если ключей меньше, чем элементов массива, то в качестве хэш-функции можно использовать деление по модулю, то есть остаток от деления целочисленного ключа Key на размерность массива HashTableSize, то есть: Key % HashTableSize
Данная функция очень проста, хотя и не относится к хорошим. Вообще, можно использовать любую размерность массива, но она должна быть такой, чтобы минимизировать число коллизий. Для этого в качестве размерности лучше использовать простое число. В большинстве случаев подобный выбор вполне удовлетворителен. Для символьной строки ключом может являться остаток от деления, например, суммы кодов символов строки на. Например,
HashTableSize = 100
∑ = 741
Ключ этой символьной строки => 741 % 100 = 7

//функция создания хеш-таблицы: //метод деления по модулю (самый //распространённый)
int Hash(int Key,int HashTableSize)
{
return Key % HashTableSize;
}

Функция середины квадрата
преобразует значение ключа в число,
возводит это число в квадрат,
из числа выбирает несколько средних цифр,
интерпретирует эти цифры как адрес записи.
Метод функции середины квадрата

Цифровое представление ключа разбивается на части, каждая из которых имеет длину, равную длине требуемого адреса.
Над частями производятся определенные арифметические или поразрядные логические операции, результат которых интерпретируется как адрес.
Например, для сравнительно небольших таблиц с ключами – символьными строками неплохие результаты дает функция хэширования, в которой адрес записи получается в результате сложения кодов символов, составляющих строку-ключ.
Метод свертки

Ключ, записанный как число в некоторой системе счисления P, интерпретируется как число в системе счисления Q>P. Обычно выбирают Q=P+1.
Это число переводится из системы Q обратно в систему P, приводится к размеру пространства записей и интерпретируется как адрес.
Функция преобразования системы счисления

Открытое хэширование
Основная идея базовой структуры при открытом (внешнем) хэшировании заключается в том, что
✵ потенциальное множество (возможно, бесконечное) разбивается на конечное число классов.
✵ для В классов, пронумерованных от 0 до В-1, строится хэш-функция h(x) такая, что для любого элемента х исходного множества функция h(x) принимает целочисленное значение из интервала 0,1,...,В-1, соответствующее классу, которому принадлежит элемент х.

Часто классы называют сегментами, поэтому будем говорить, что элемент х принадлежит сегменту h(x).
Массив, называемый таблицей сегментов и проиндексированный номерами сегментов 0,1,...,В-1, содержит заголовки для B списков.
Элемент х, относящийся к i-му списку – это элемент исходного множества, для которого
h(x)=i
Если сегменты примерно одинаковы по размеру, то в этом случае списки всех сегментов должны быть наиболее короткими при данном числе сегментов. Если исходное множество состоит из N элементов, тогда средняя длина списков будет N/B элементов.
Если можно оценить величину N и выбрать В как можно ближе к этой величине, то в каждом списке будет один или два элемента. Тогда время выполнения операторов словарей будет малой постоянной величиной, не зависящей от N.

//Пример 1. Программная реализация открытого хэширования.
#include
#include
using namespace std;
typedef int T; // тип элементов
typedef int hashTableIndex; // индекс в хэш-таблице
#define compEQ(a,b) (a = = b)
typedef struct Node_
{ T data; // данные, хранящиеся в вершине struct Node_ *next; // следующая вершина
} Node;
Node **hashTable;
int hashTableSize;
hashTableIndex myhash(T data);
Node *insertNode(T data);
void deleteNode(T data);
Node *findNode (T data);
//************функция размещения вершины**************
hashTableIndex myhash(T data)
{
return (data % hashTableSize);
}

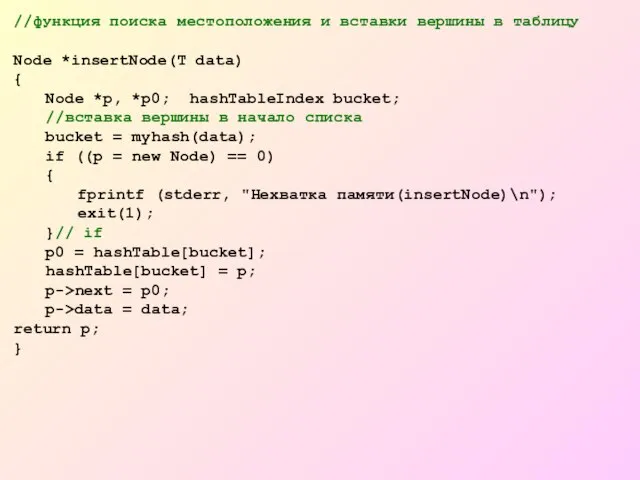
//функция поиска местоположения и вставки вершины в таблицу
Node *insertNode(T data)
{
Node *p, *p0; hashTableIndex bucket;
//вставка вершины в начало списка
bucket = myhash(data);
if ((p = new Node) == 0)
{
fprintf (stderr, "Нехватка памяти(insertNode)\n");
exit(1);
}// if
p0 = hashTable[bucket];
hashTable[bucket] = p;
p->next = p0;
p->data = data;
return p;
}

//функция удаления вершины из таблицы
void deleteNode(T data)
{
Node *p0, *p;
hashTableIndex bucket;
p0 = 0;
bucket = myhash(data);
p = hashTable[bucket];
while (p && !compEQ(p->data, data))
{
p0 = p; p = p->next;
}
if (!p) return;
if (p0) p0->next = p->next;
else hashTable[bucket] = p->next;
free (p);
}

//функция поиска вершины со значением
Node *findNode (T data)
{
Node *p;
p = hashTable[myhash(data)];
while (p && !compEQ(p->data, data))
p = p->next;
return p;
}
//***********************************************

int main()
{
int i, *a, maxnum;
cout << "Введите количество элементов maxnum : ";
cin >> maxnum;
cout << "Введите размер хэш-таблицы HashTableSize: ";
cin >> hashTableSize;
a = new int[maxnum];
hashTable = new Node*[hashTableSize]; //выделить память
for (i = 0; i < hashTableSize; i++)
hashTable[i] = NULL;
//генерация массива случайных чисел
for (i = 0; i < maxnum; i++) a[i] = rand();
//заполнение хэш-таблицы элементами массива
for (i = 0; i < maxnum; i++)
insertNode(a[i]);
//поиск элементов массива хэш-таблице
for (i = maxnum-1; i >= 0; i--) findNode(a[i]);

// вывод эдементов массива в файл List.txt
ofstream out("List.txt");
for (i = 0; i < maxnum; i++)
{
out << a[i];
if ( i < maxnum - 1 ) out << "\t";
}
out.close();
// сохранение хэш-таблицы в файл HashTable.txt
out.open("HashTable.txt");
for (i = 0; i < hashTableSize; i++)
{
out << i << " : ";
Node *Temp = hashTable[i];
while ( Temp )
{
out << Temp->data << " -> ";
Temp = Temp->next;
}
out << endl;
} //for
out.close();

//очистка хэш-таблицы
for (i = maxnum-1; i >= 0; i--) deleteNode(a[i]);
return 0;
}
50 элементов и размер таблицы 10
10 элементов и размер таблицы тоже 10
25 элементов и размер таблицы 5

Закрытое хеширование
При закрытом (внутреннем) хэшировании в хэш-таблице хранятся непосредственно сами элементы, а не заголовки списков элементов. Поэтому в каждой записи (сегменте) может храниться только один элемент.
При закрытом хэшировании применяется методика повторного хэширования:
Если осуществляется попытка поместить элемент х в сегмент с номером h(х), который уже занят другим элементом (коллизия), то в соответствии с методикой повторного хэширования выбирается последовательность других номеров сегментов h1(х),h2(х),..., куда можно поместить элемент х.
Каждое из этих местоположений последовательно проверяется, пока не будет найдено свободное. Если свободных сегментов нет, то, следовательно, таблица заполнена, и элемент х добавить нельзя.

При поиске элемента х необходимо просмотреть все местоположения h(x),h1(х),h2(х),..., пока не будет найден х или пока не встретится пустой сегмент. Чтобы объяснить, почему можно остановить поиск при достижении пустого сегмента, предположим, что в хэш-таблице не допускается удаление элементов. Пусть h3(х) – первый пустой сегмент. В такой ситуации невозможно нахождение элемента х в сегментах h4(х),h5(х) и далее, так как при вставке элемент х вставляется в первый пустой сегмент, следовательно, он находится где-то до сегмента h3(х).

Если в хэш-таблице допускается удаление элементов, то при достижении пустого сегмента, не найдя элемента х, нельзя быть уверенным в том, что его вообще нет в таблице, т.к. сегмент может стать пустым уже после вставки элемента х. Поэтому, чтобы увеличить эффективность данной реализации, необходимо в сегмент, который освободился после операции удаления элемента, поместить специальную константу, которую назовем, например, DEL. В качестве альтернативы специальной константе можно использовать дополнительное поле таблицы, которое показывает состояние элемента.

Важно различать константы DEL и NULL – последняя находится в сегментах, которые никогда не содержали элементов. При таком подходе выполнение поиска элемента не требует просмотра всей хэш-таблицы. Кроме того, при вставке элементов сегменты, помеченные константой DEL, можно трактовать как свободные, таким образом, пространство, освобожденное после удаления элементов, можно рано или поздно использовать повторно.
Но, если невозможно непосредственно сразу после удаления элементов пометить освободившиеся сегменты, то следует предпочесть закрытому хэшированию схему открытого хеширования.
Существует несколько методов повторного хэширования, то есть определения местоположений h(x),h1(х),h2(х),...:
линейное опробование;
квадратичное опробование;
двойное хэширование.

Линейное опробование
Это последовательный перебор сегментов таблицы с некоторым фиксированным шагом:
адрес=h(x)+ci, где i – номер попытки разрешить коллизию;
c – константа, определяющая шаг перебора.
При шаге, равном единице, происходит последовательный перебор всех сегментов после текущего.

Квадратичное опробование
отличается от линейного тем, что шаг перебора сегментов нелинейно зависит от номера попытки найти свободный сегмент:
адрес=h(x)+ci+di2, где i – номер попытки разрешить коллизию,
c и d – константы. Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов.
Однако, даже относительно небольшое число проб может быстро привести к выходу за адресное пространство небольшой таблицы вследствие квадратичной зависимости адреса от номера попытки.

Двойное хэширование
Основана на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хэш-функций:
адрес=h(x)+ih2(x).
Очевидно, что по мере заполнения хэш-таблицы будут происходить коллизии, и в результате их разрешения очередной адрес может выйти за пределы адресного пространства таблицы.
Чтобы это явление происходило реже, можно пойти на увеличение длины таблицы по сравнению с диапазоном адресов, выдаваемым хэш-функцией. С одной стороны, это приведет к сокращению числа коллизий и ускорению работы с хэш-таблицей, а с другой – к нерациональному расходованию памяти.
Даже при увеличении длины таблицы в два раза по сравнению с областью значений хэш-функции нет гарантии того, что в результате коллизий адрес не превысит длину таблицы. При этом в начальной части таблицы может оставаться достаточно свободных сегментов.
Поэтому на практике используют циклический переход к началу таблицы.

В случае многократного превышения адресного пространства и, соответственно, многократного циклического перехода к началу будет происходить просмотр одних и тех же ранее занятых сегментов, тогда как между ними могут быть еще свободные сегменты. Более корректным будет использование сдвига адреса на 1 в случае каждого циклического перехода к началу таблицы. Это повышает вероятность нахождения свободных сегментов.
В случае применения схемы закрытого хэширования скорость выполнения вставки и других операций зависит не только от равномерности распределения элементов по сегментам хэш-функцией, но и от выбранной методики повторного хэширования (опробования) для разрешения коллизий, связанных с попытками вставки элементов в уже заполненные сегменты.

Например, методика линейного опробования для разрешения коллизий – не самый лучший выбор:
Как только несколько последовательных сегментов будут заполнены, образуя группу, любой новый элемент при попытке вставки в эти сегменты будет вставлен в конец этой группы, увеличивая тем самым длину группы последовательно заполненных сегментов.
Другими словами, для поиска пустого сегмента в случае непрерывного расположения заполненных сегментов необходимо просмотреть больше сегментов, чем при случайном распределении заполненных сегментов.
Отсюда также следует очевидный вывод, что при непрерывном расположении заполненных сегментов увеличивается время выполнения вставки нового элемента и других операций.

//Пример 2. Программная реализация закрытого хеширования.
#include
#include
using namespace std;
typedef int T; // тип элементов
typedef int hashTableIndex; // индекс в хеш- //таблице
int hashTableSize;
T *hashTable; //указатель на таблицу
bool *used;
hashTableIndex myhash(T data);
void insertData(T data);
void deleteData(T data);
bool findData (T data);
int dist (hashTableIndex a,hashTableIndex b);

int _tmain(int argc, _TCHAR* argv[])
{
int i, *a, maxnum;
cout << "Введите количество элементов maxnum : ";
cin >> maxnum;
cout << "Введите размер хеш-таблицы hashTableSize : ";
cin >> hashTableSize;
a = new int[maxnum];
hashTable = new T[hashTableSize];

//выделить память
used = new bool[hashTableSize];
//выделить память для флажков
//заполнение нулями
for (i = 0; i < hashTableSize; i++)
{ hashTable[i] = 0; used[i] = false; }
// генерация массива
for (i = 0; i < maxnum; i++) a[i] = rand();
// заполнение хеш-таблицы элементами массива
for (i = 0; i < maxnum; i++) insertData(a[i]);
// поиск элементов массива по хеш-таблице
for (i = maxnum-1; i >= 0; i--) findData(a[i]);
// вывод элементов массива в файл List.txt
ofstream out("List.txt");
for (i = 0; i < maxnum; i++)
{ out << a[i];
if ( i < maxnum - 1 ) out << "\t";
}
out.close();
// сохранение хеш-таблицы в файл HashTable.txt
out.open("HashTable.txt");
for (i = 0; i < hashTableSize; i++)
{ out << i << " : " << used[i] << " : " << hashTable[i] << endl; } out.close();

// очистка хеш-таблицы
for (i = maxnum-1; i >= 0; i--)
{ deleteData(a[i]); }
system("pause");
return 0;}
// хеш-функция размещения величины
hashTableIndex myhash(T data)
{ return (data % hashTableSize);}
// функция поиска местоположения и вставки величины в таблицу
void insertData(T data)
{ hashTableIndex bucket;
bucket = myhash(data);
while ( used[bucket] && hashTable[bucket] != data)
bucket = (bucket + 1) % hashTableSize;
if ( !used[bucket] )
{ used[bucket] = true;
hashTable[bucket] = data;
}
}

// функция поиска величины, равной data
bool findData (T data)
{ hashTableIndex bucket;
bucket = myhash(data);
while ( used[bucket] && hashTable[bucket] != data )
bucket = (bucket + 1) % hashTableSize;
return used[bucket] && hashTable[bucket] == data;
}
//функция удаления величины из таблицы
void deleteData(T data)
{ int bucket, gap;
bucket = myhash(data);
while ( used[bucket] && hashTable[bucket] != data )
bucket = (bucket + 1) % hashTableSize;
if ( used[bucket] && hashTable[bucket] == data )
{ //1
used[bucket] = false;
gap = bucket;
bucket = (bucket + 1) % hashTableSize;
while ( used[bucket] )
{ if ( bucket == myhash(hashTable[bucket]) )

bucket = (bucket + 1) % hashTableSize;
else
if(dist(myhash(hashTable[bucket]),bucket) < dist(gap,bucket) )
bucket = (bucket + 1) % hashTableSize;
else
{used[gap] = true;
hashTable[gap] = hashTable[bucket];
used[bucket] = false;
gap = bucket;
bucket++;
}
}// while
} //1
} //deleteData
// функция вычисления расстояния от a до b (по часовой стрелке, слева
// направо)
int dist (hashTableIndex a, hashTableIndex b)
{
return (b - a + hashTableSize) % hashTableSize;
}

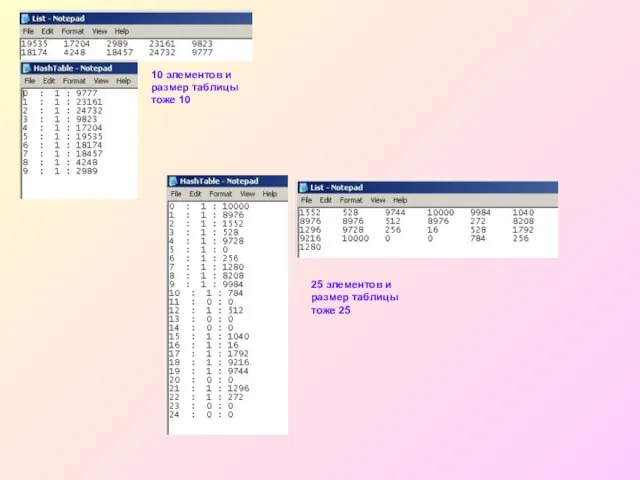
25 элементов и размер таблицы тоже 25
10 элементов и размер таблицы тоже 10

До сих пор рассматривались способы поиска в таблице по ключам, позволяющим однозначно идентифицировать запись.
Такие ключи называются первичными.
Возможен вариант организации таблицы, при котором отдельный ключ не позволяет однозначно идентифицировать запись. Такая ситуация часто встречается в базах данных. Идентификация записи осуществляется по некоторой совокупности ключей.
Ключи, не позволяющие однозначно идентифицировать запись в таблице, называются вторичными ключами. Даже при наличии первичного ключа, для поиска записи могут быть использованы вторичные.

Ключевые термины:
Вторичные ключи – это ключи, не позволяющие однозначно идентифицировать запись в таблице.
Закрытое хэширование или Метод открытой адресации – это технология разрешения коллизий, которая предполагает хранение записей в самой хэш-таблице.
Коллизия – это ситуация, когда разным ключам соответствует одно значение хэш-функции.
Коэффициент заполнения хэш-таблицы – это количество хранимых элементов массива, деленное на число возможных значений хэш-функции.
Открытое хеширование или Метод цепочек – это технология разрешения коллизий, которая состоит в том, что элементы множества с равными хэш-значениями связываются в цепочку-список.
Первичные ключи – это ключи, позволяющие однозначно идентифицировать запись.
Повторное хеширование – это поиск местоположения для очередного элемента таблицы с учетом шага перемещения.

Пространство записей – это множество тех ячеек памяти, которые выделяются для хранения таблицы.
Пространство ключей – это множество всех теоретически возможных значений ключей записи.
Синонимы – это совпадающие ключи в хэш-таблице.
Хеширование – это преобразование входного массива данных определенного типа и произвольной длины в выходную битовую строку фиксированной длины.
Хеш-таблица – это структура данных, реализующая интерфейс ассоциативного массива, то есть она позволяет хранить пары вида "ключ- значение" и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.
Хэш-таблицы с прямой адресацией – это хэш-таблицы, использующие инъективные хэш-функции и не нуждающиеся в механизме разрешения коллизий.

Контрольные вопросы
Каков принцип построения хеш-таблиц?
Существуют ли универсальные методы построения хеш-таблиц?
Почему возможно возникновение коллизий?
Каковы методы устранения коллизий? Охарактеризуйте их эффективность в различных ситуациях.
Назовите преимущества открытого и закрытого хеширования.
В каком случае поиск в хеш-таблицах становится неэффективен?
Как выбирается метод изменения адреса при повторном хешировании?