Ichakaev_kursovaya

ДАННЫЕ

СГЛАЖИВАНИЕ
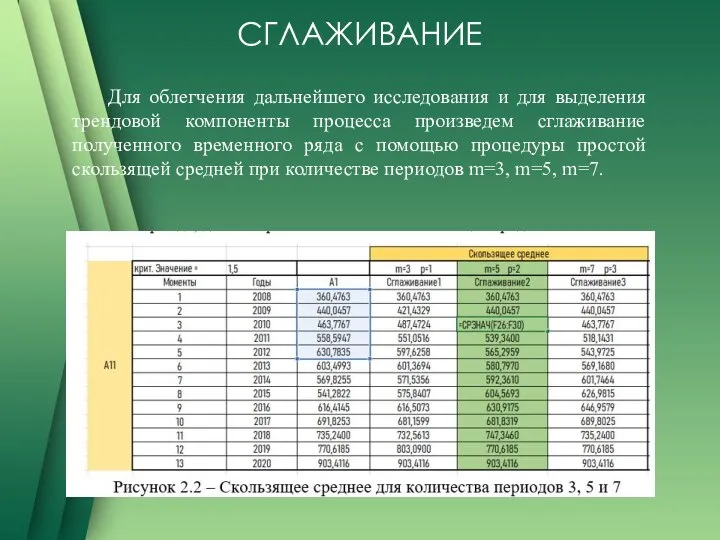
Для облегчения дальнейшего исследования и для выделения трендовой компоненты процесса произведем сглаживание полученного временного ряда с помощью процедуры простой скользящей средней при количестве периодов m=3, m=5, m=7.

СГЛАЖИВАНИЕ. ГРАФИКИ
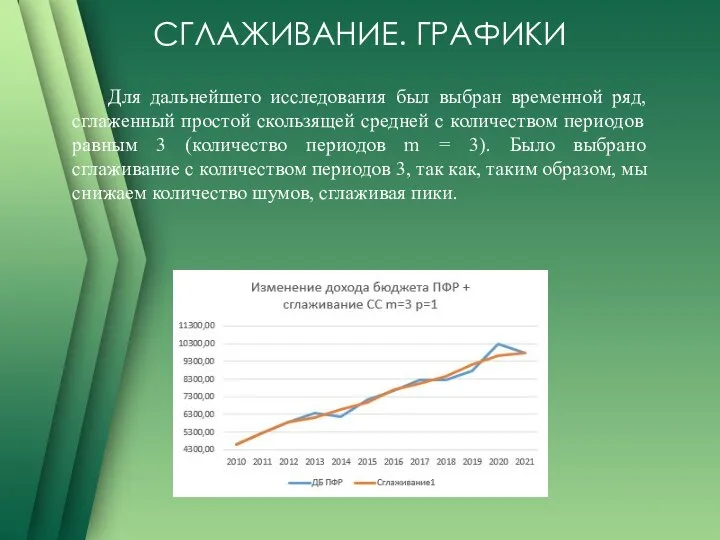
Для дальнейшего исследования был выбран временной ряд, сглаженный простой скользящей средней с количеством периодов равным 3 (количество периодов m = 3). Было выбрано сглаживание с количеством периодов 3, так как, таким образом, мы снижаем количество шумов, сглаживая пики.

МОДЕЛЬ КРИВОЙ РОСТА
Воспользуемся надстройкой Анализ данных, инструментом анализа Регрессия и получим коэффициенты модели кривой роста. Проверим их значимость при уровне значимости 0,05. Коэффициенты выделены красным.

ПРОВЕРКА УСЛОВИЙ ГАУССА-МАРКОВА
Для того чтобы регрессионный анализ давал наилучшие из всех возможных результаты, случайная ошибка должна удовлетворять определенным условиям, известным как условия Гаусса-Маркова.
Наиболее важными свойствами остатков являются равенство математического ожидания нулю, независимость последовательных уровней ряда остатков, их случайность и соответствие нормальному закону распределения.

ПРОВЕРКА УСЛОВИЙ ГАУССА-МАРКОВА
Наличие автокорреляции говорит о том, что каждое следующее значение остатков зависит от предшествующих. По одной из причин, может быть отсутствие фактора, оказывающего существенное влияние на результат, но влияние которого отражается в остатках.
Модель удовлетворяет нормальному распределению.

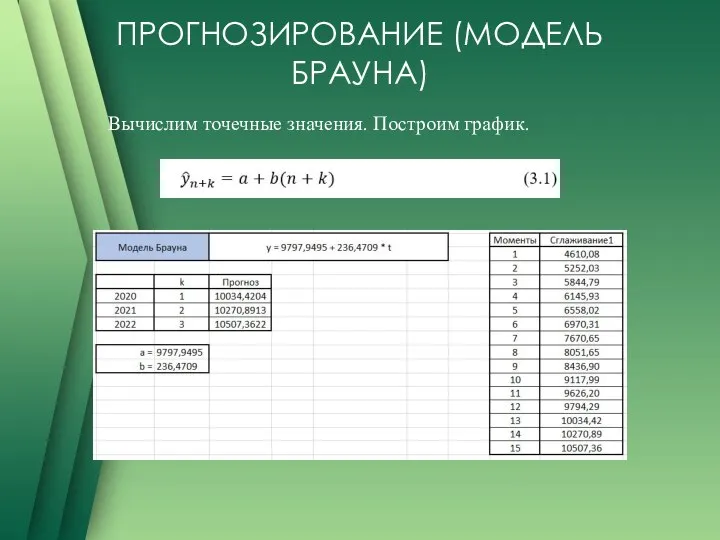
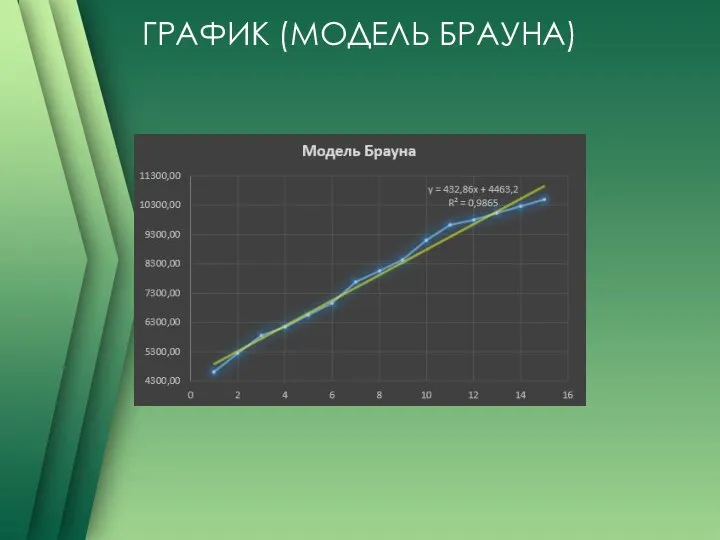
МОДЕЛЬ БРАУНА
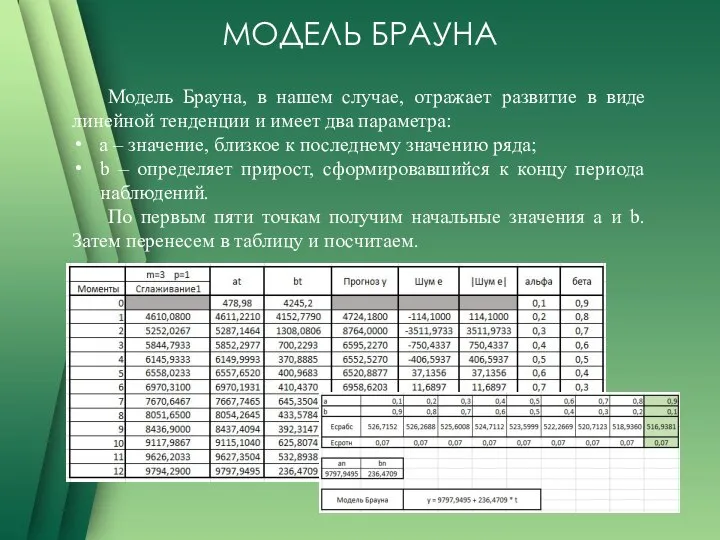
Модель Брауна, в нашем случае, отражает развитие в виде линейной тенденции и имеет два параметра:
a – значение, близкое к последнему значению ряда;
b – определяет прирост, сформировавшийся к концу периода наблюдений.
По первым пяти точкам получим начальные значения а и b. Затем перенесем в таблицу и посчитаем.

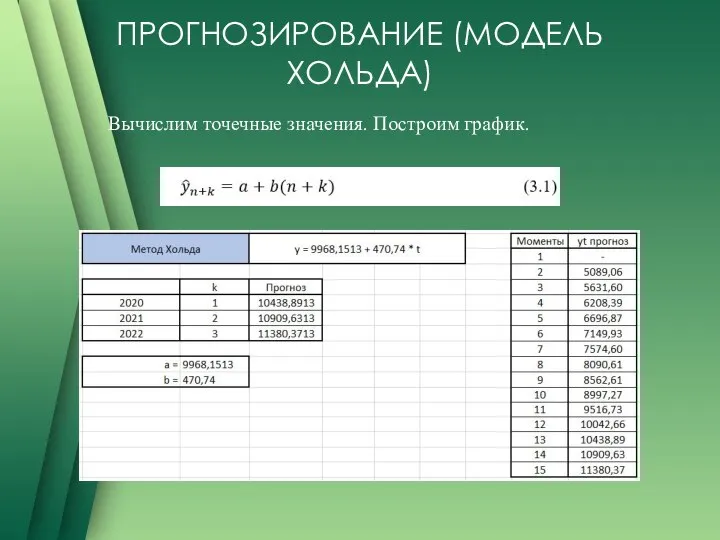
МОДЕЛЬ ПО МЕТОДУ ХОЛЬДА
Вид экспоненциального сглаживания, двухпараметрический способ сглаживания (метод Хольда) включает два уравнения. Первое предназначено для сглаживания наблюдённых значений, а второе – для сглаживания тренда. Двухпараметрическое сглаживание, потому что учитывается значение времени и тренда.
Получим более точную оценку начального значения b, используя первые 5 наблюдений ряда.

ГРАФИК (МОДЕЛЬ КРИВОЙ РОСТА)
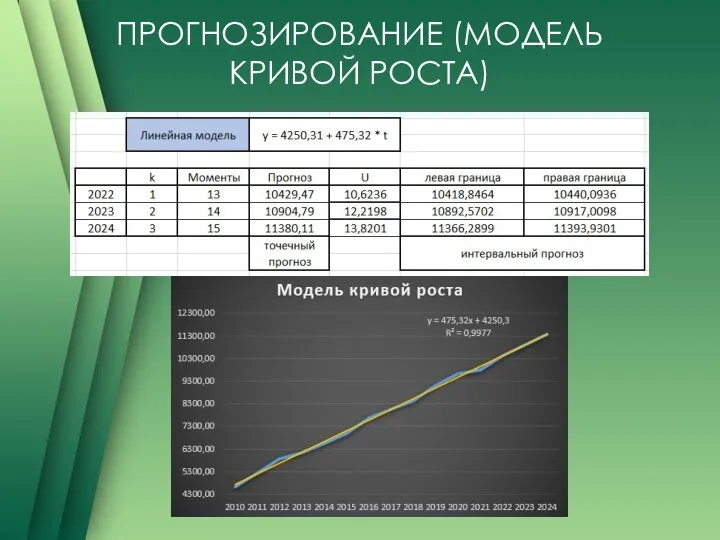
Вычислим точечные значения, вычислим значение U и получим доверительный интервал прогноз. Построим график.

ПРОГНОЗИРОВАНИЕ (МОДЕЛЬ КРИВОЙ РОСТА)

ПРОГНОЗИРОВАНИЕ (МОДЕЛЬ БРАУНА)
Вычислим точечные значения. Построим график.

ГРАФИК (МОДЕЛЬ БРАУНА)

ПРОГНОЗИРОВАНИЕ (МОДЕЛЬ ХОЛЬДА)
Вычислим точечные значения. Построим график.

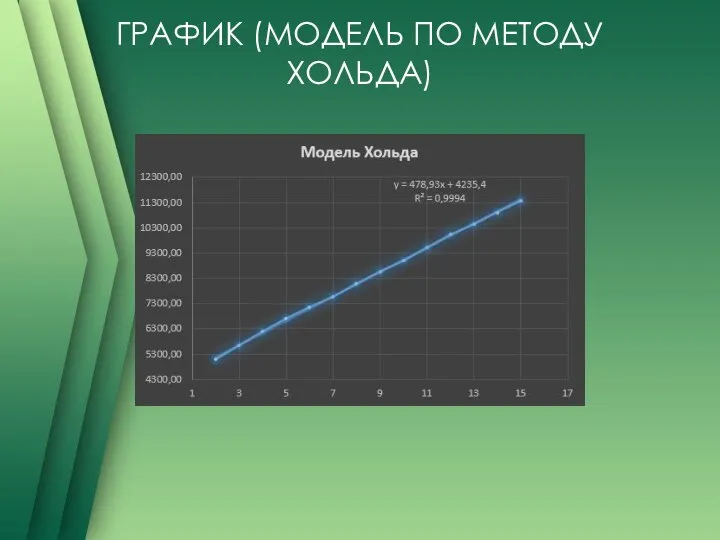
ГРАФИК (МОДЕЛЬ ПО МЕТОДУ ХОЛЬДА)