Содержание
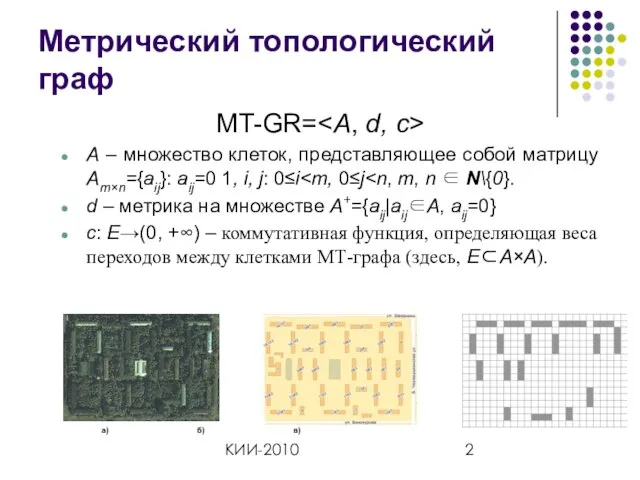
- 2. КИИ-2010 Метрический топологический граф MT-GR= A – множество клеток, представляющее собой матрицу Am×n={aij}: aij=0 1, i,
- 3. КИИ-2010 Пусть aij, alk Am×n: aij≠alk , aij≠0, alk≠0. Путем из aij в alk будем называть
- 4. КИИ-2010 МТ-граф. Основные определения 2. Две различные клетки МТ-графа ai1j1, ai2j2 Am×n будем называть смежными, если
- 5. КИИ-2010 МТ-граф. Основные определения 3. d(aij, alk)=H(aij, alk)= Δi=Δi(aij, alk)=|i-l| Δj=Δj(aij, alk)=|j-k|
- 6. КИИ-2010 Задача планирования траектории PTask=〈MT-Gr, astartI startJ, agoalI goalJ〉 π(astartI startJ, agoalI goalJ) Решение задачи планирования
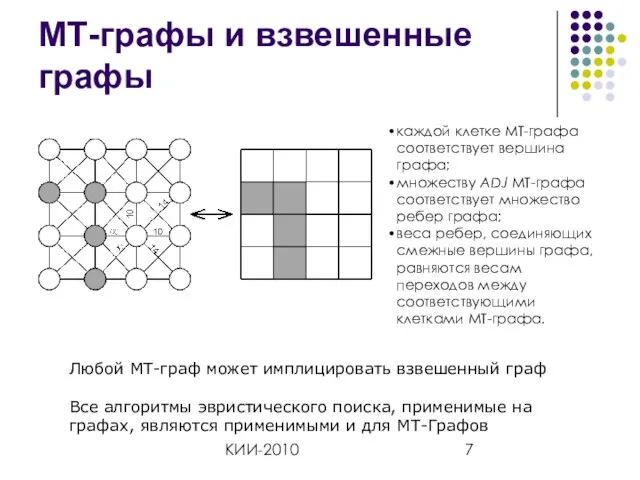
- 7. КИИ-2010 МТ-графы и взвешенные графы Любой МТ-граф может имплицировать взвешенный граф Все алгоритмы эвристического поиска, применимые
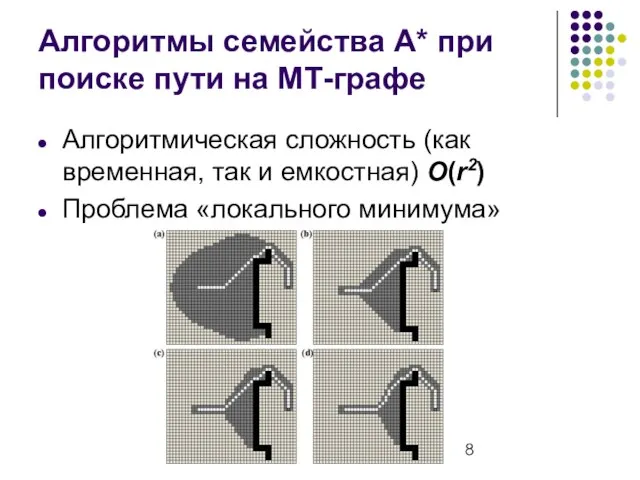
- 8. КИИ-2010 Алгоритмы семейства A* при поиске пути на МТ-графе Алгоритмическая сложность (как временная, так и емкостная)
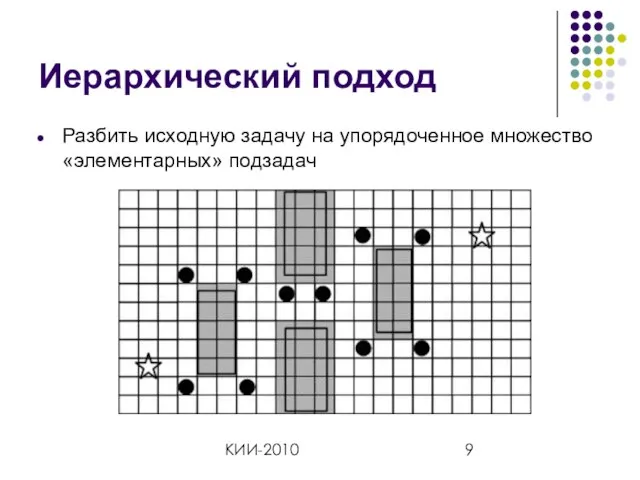
- 9. КИИ-2010 Иерархический подход Разбить исходную задачу на упорядоченное множество «элементарных» подзадач
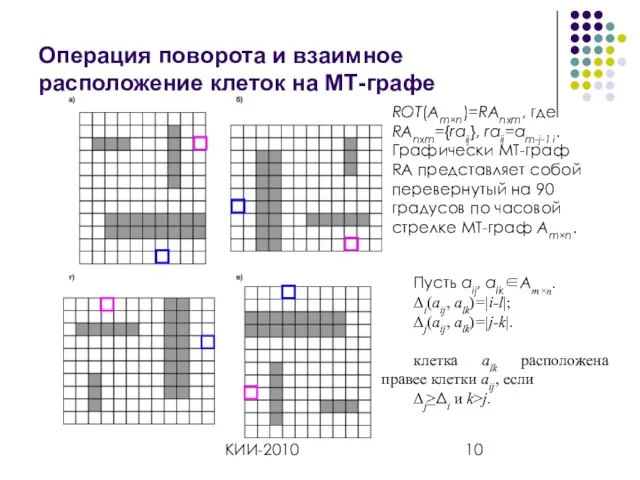
- 10. КИИ-2010 Операция поворота и взаимное расположение клеток на МТ-графе ROT(Am×n)=RAnxm, где RAnxm={raij}, raij=am-j-1 i. Графически МТ-граф
- 11. КИИ-2010 Нуль-траектория Нуль-траекторией между двумя различными клетками aij и alk будем называть последовательность смежных клеток МТ-графа
- 12. КИИ-2010 Препятствие Препятствия Obs={ai0j0, ai1j1, ai2j2, …, aisjs|аikjk=1, аikjk∈adj(аik-1jk-1) ∀k=0,1,2, …, s, s∈N}. Препятствие Obs лежит
- 13. КИИ-2010 Секция Секция - упорядоченная пара клеток МТ-графа Секция проходима ТТТК нуль-траектория tr(aij, akl) проходима Вес
- 14. КИИ-2010 Задача планирования Пусть на заданном МТ-графе MT-Gr зафиксированы начальная astartI startJ и целевая agoalI goalJ
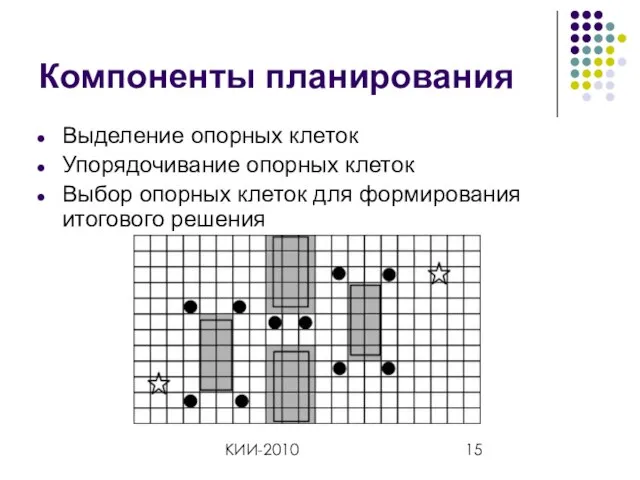
- 15. КИИ-2010 Компоненты планирования Выделение опорных клеток Упорядочивание опорных клеток Выбор опорных клеток для формирования итогового решения
- 16. КИИ-2010 Вероятностный иерархический алгоритм планирования траектории Вход: PPС={PP={astartI startJ , agoalI goalJ }} – множество частичных
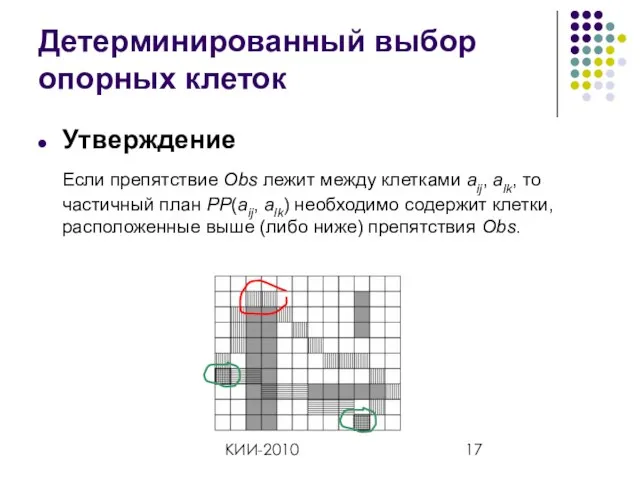
- 17. КИИ-2010 Детерминированный выбор опорных клеток Утверждение Если препятствие Obs лежит между клетками aij, alk, то частичный
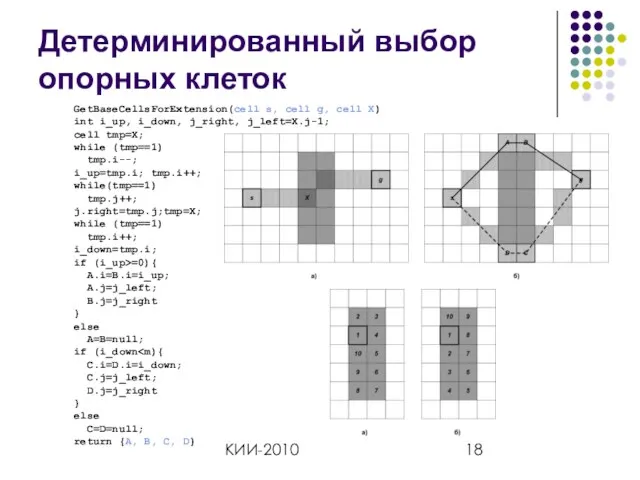
- 18. КИИ-2010 Детерминированный выбор опорных клеток GetBaseCellsForExtension(cell s, cell g, cell X) int i_up, i_down, j_right, j_left=X.j-1;
- 19. КИИ-2010 HGA* Вход: PPС={PP={astartI startJ , agoalI goalJ }} Шаг 1. Выбрать лучший частичный путь PP
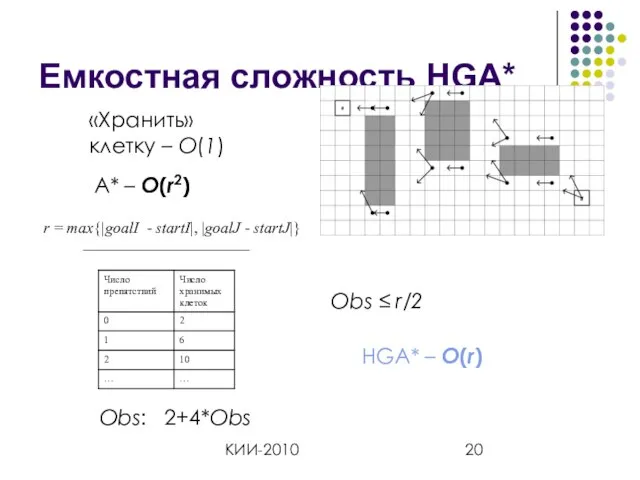
- 20. КИИ-2010 Емкостная сложность HGA* «Хранить» клетку – O(1) A* – O(r2) Obs: 2+4*Obs Obs ≤ r/2
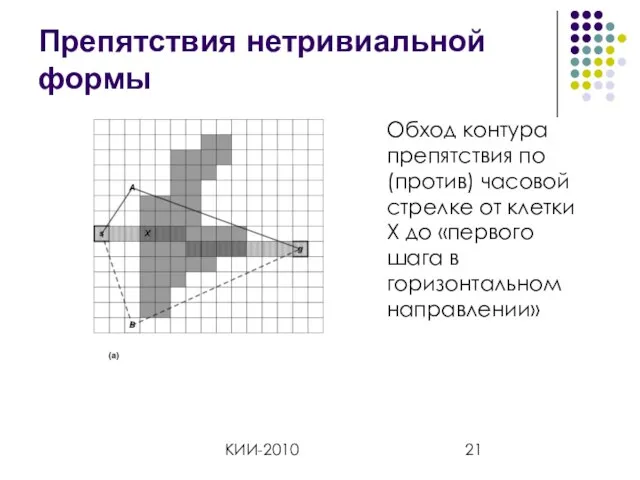
- 21. КИИ-2010 Препятствия нетривиальной формы Обход контура препятствия по (против) часовой стрелке от клетки X до «первого
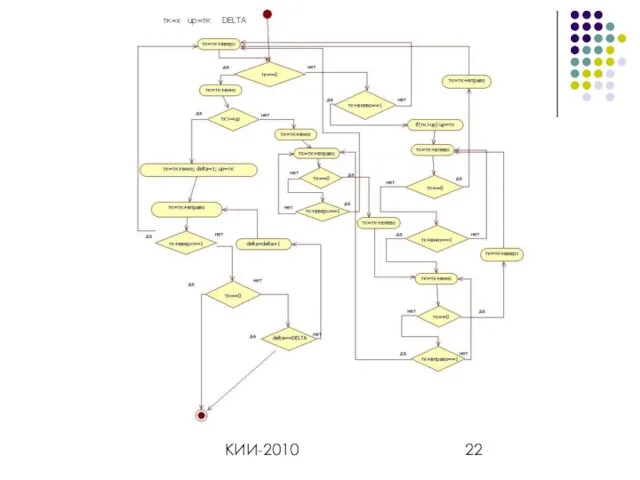
- 22. КИИ-2010
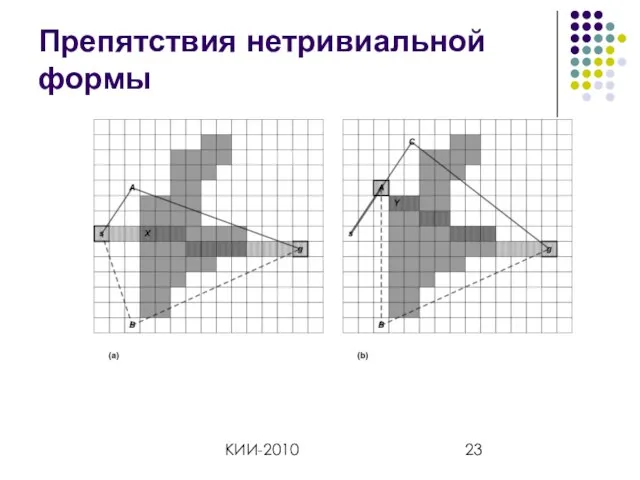
- 23. КИИ-2010 Препятствия нетривиальной формы
- 24. КИИ-2010 Экспериментальные результаты. 3 серии экспериментов МТ-графы различных размеров с различной степенью заполнения препятствиями МТ-графы –
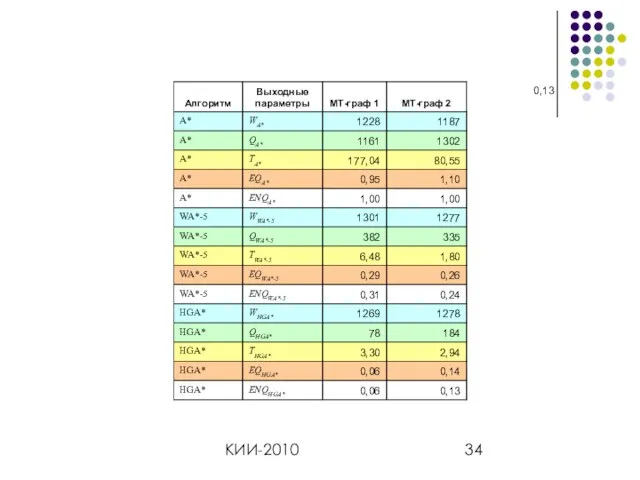
- 25. КИИ-2010 Экспериментальные результаты. Алгоритмы HGA*, A*, WA*-3, WA*-5 Отслеживаемые индикаторы Q – число сохраненных клеток W
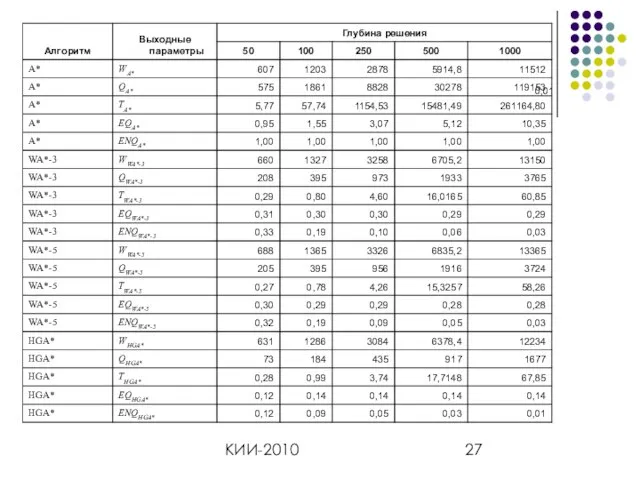
- 26. КИИ-2010 1 серия экспериментов. λ=[(l⋅2+d⋅4)⋅N]/(m⋅n)
- 27. КИИ-2010 0,01
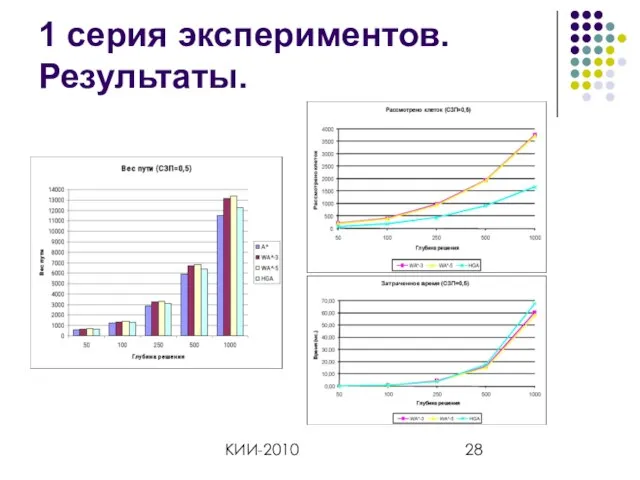
- 28. КИИ-2010 1 серия экспериментов. Результаты.
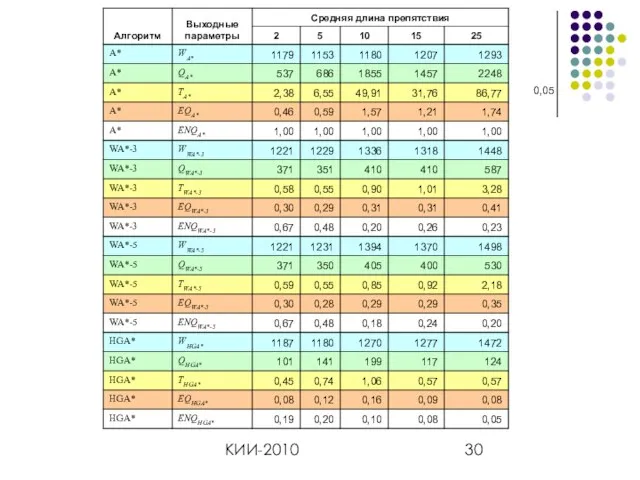
- 29. КИИ-2010 2 серия экспериментов Размер МТ-графа фиксирован 101х101 Глубина решения фиксирована 100 СЗП фиксирована λ =
- 30. КИИ-2010 0,05
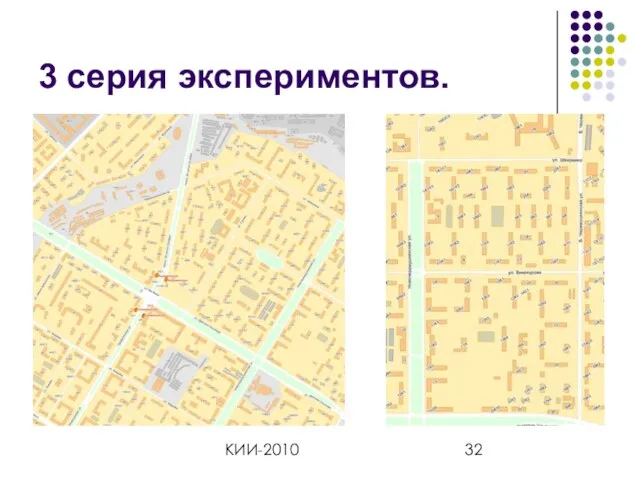
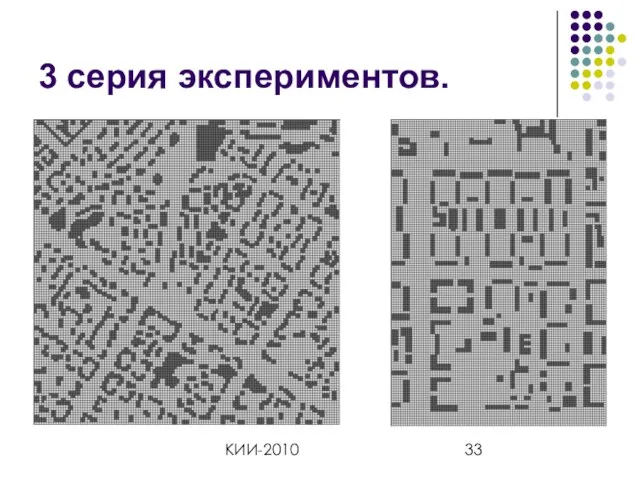
- 31. КИИ-2010 3 серия экспериментов. Маловысотный полет вертолета. 2 МТ-графа (цифровые карты местности Москвы, 2х2 км) Глубина
- 32. КИИ-2010 3 серия экспериментов.
- 33. КИИ-2010 3 серия экспериментов.
- 34. КИИ-2010 0,13
- 35. КИИ-2010 Выводы по результатам экспериментов HGA* использует вычислительные ресурсы гораздо эффективней аналогов HGA* лучше масштабируется HGA*
- 37. Скачать презентацию












![КИИ-2010 1 серия экспериментов. λ=[(l⋅2+d⋅4)⋅N]/(m⋅n)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460516/slide-25.jpg)



 Стандарты и спецификации в области информационной безопасности
Стандарты и спецификации в области информационной безопасности Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров
Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров С днём рождения, Мамочка
С днём рождения, Мамочка Себестоимость. Формула
Себестоимость. Формула Презентация на тему Все профессии важны (2 класс)
Презентация на тему Все профессии важны (2 класс) Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА
Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА Подходы к менеджменту: системный, ситуационный, процессный
Подходы к менеджменту: системный, ситуационный, процессный ProSpace (Казахстан)
ProSpace (Казахстан) Технология создания gif-анимации в Photoshop или ImageReady
Технология создания gif-анимации в Photoshop или ImageReady Эмпатическое слушание
Эмпатическое слушание vydacha_zadaniy (1) (1)
vydacha_zadaniy (1) (1) Отделка - это завершающая операция при изготовлении изделий
Отделка - это завершающая операция при изготовлении изделий Правотворческая деятельность на муниципальном уровне:
Правотворческая деятельность на муниципальном уровне: Пастернак Борис Леонидович ( 1890 - 1960 )
Пастернак Борис Леонидович ( 1890 - 1960 ) Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике
Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике  Dr.Web Enterprise Suite
Dr.Web Enterprise Suite Социальный контекст инновационного развития
Социальный контекст инновационного развития РМО учителей биологии и экологии
РМО учителей биологии и экологии Differences_between_British_and_American_versions_of_English_2 (2)
Differences_between_British_and_American_versions_of_English_2 (2) Диверсификация профессиональных навыков разработчикаДмитрий Васильев
Диверсификация профессиональных навыков разработчикаДмитрий Васильев Урок технологии
Урок технологии Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс
Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс Грузинский Технический Университет. Тбилиси
Грузинский Технический Университет. Тбилиси Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения
Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения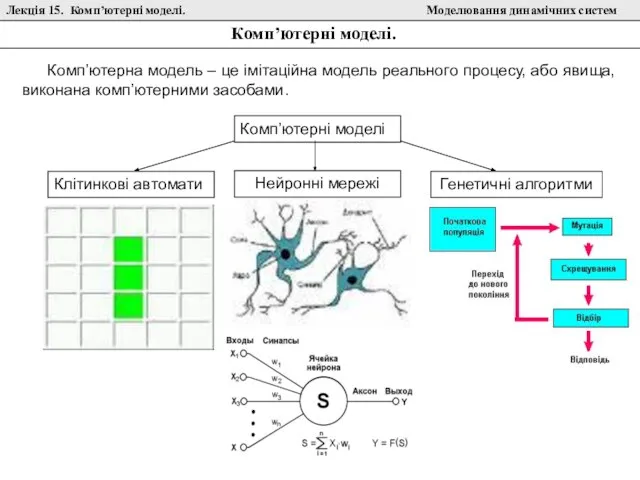 Клітинкові автомати
Клітинкові автомати Универсальная система учёта и паспортизации
Универсальная система учёта и паспортизации Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади
Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади