Информационные модели. Графы

Впервые основы теории графов появились в работах Леонарда Эйлера (1707-1783; швейцарский, немецкий и российский математик) , в которых он описывал решение головоломок и математических развлекательных задач.
Теория графов началась с решения Эйлером задачи о семи мостах Кёнигсберга.

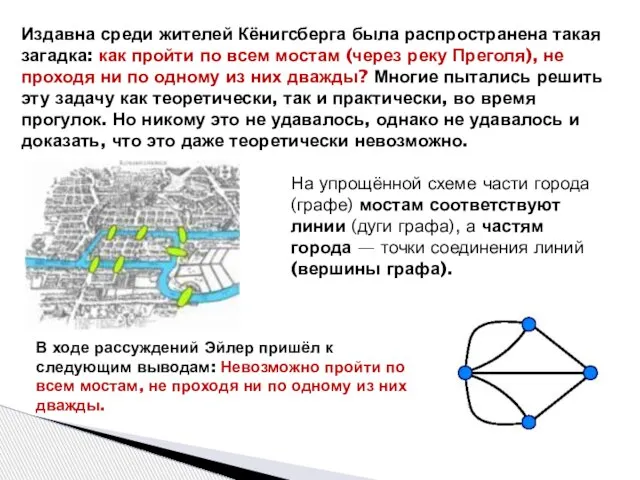
Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды? Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.
На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа).
В ходе рассуждений Эйлер пришёл к следующим выводам: Невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

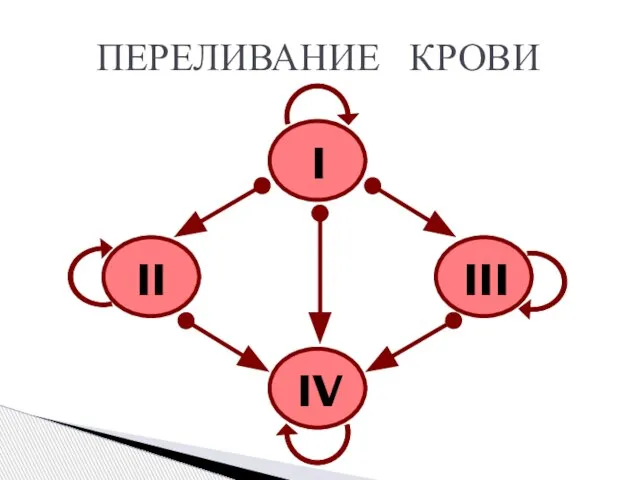
Существуют 4 группы крови. При переливании крови от одного человека к другому не все группы совместимы. Но известно, что одинаковые группы можно переливать от человека к человеку, т.е.
1 – 1, 2 – 2 и т.д.
А также 1 группу можно переливать всем остальным группам,
2 и 3 группу только 4 группе.
Задача.

ПЕРЕЛИВАНИЕ КРОВИ

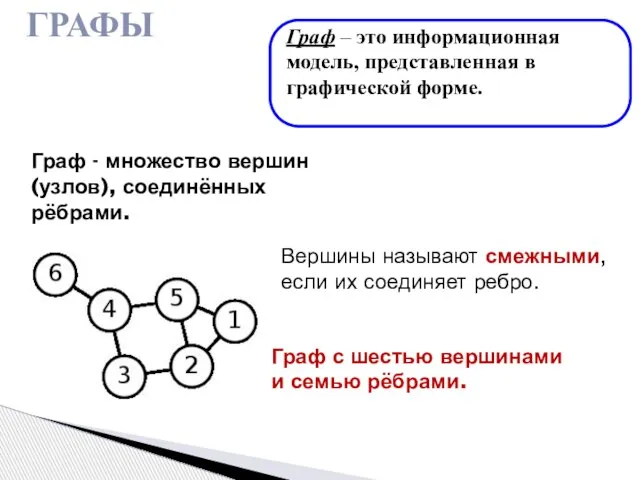
Графы
Граф – это информационная модель, представленная в графической форме.
Граф - множество вершин (узлов), соединённых рёбрами.
Граф с шестью вершинами и семью рёбрами.
Вершины называют смежными, если их соединяет ребро.

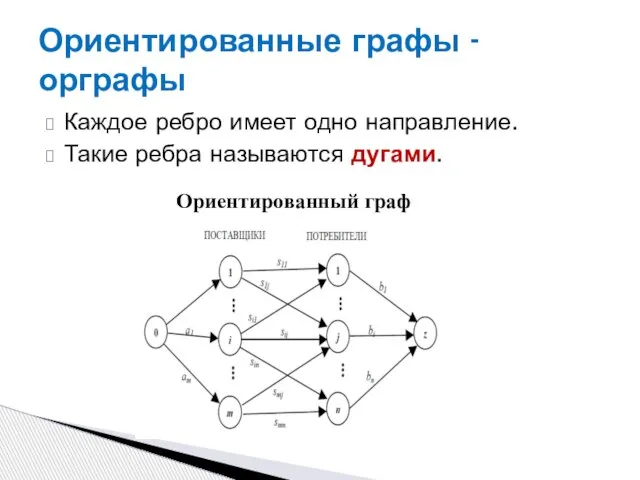
Ориентированные графы - орграфы
Каждое ребро имеет одно направление.
Такие ребра называются дугами.
Ориентированный граф

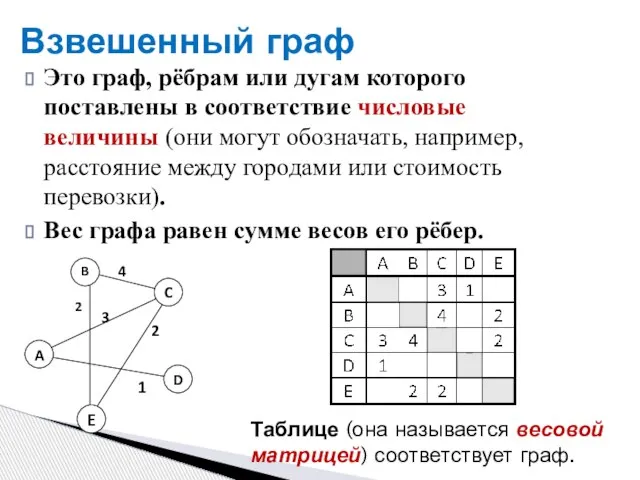
Взвешенный граф
Это граф, рёбрам или дугам которого поставлены в соответствие числовые величины (они могут обозначать, например, расстояние между городами или стоимость перевозки).
Вес графа равен сумме весов его рёбер.
Таблице (она называется весовой матрицей) соответствует граф.

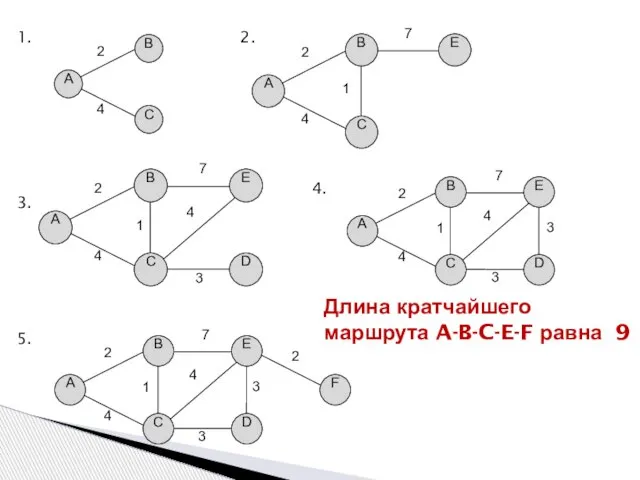
Задача
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
1) 9 2) 10 3) 11 4) 12

1.
2.
3.
4.
5.
Длина кратчайшего маршрута A-B-C-E-F равна 9

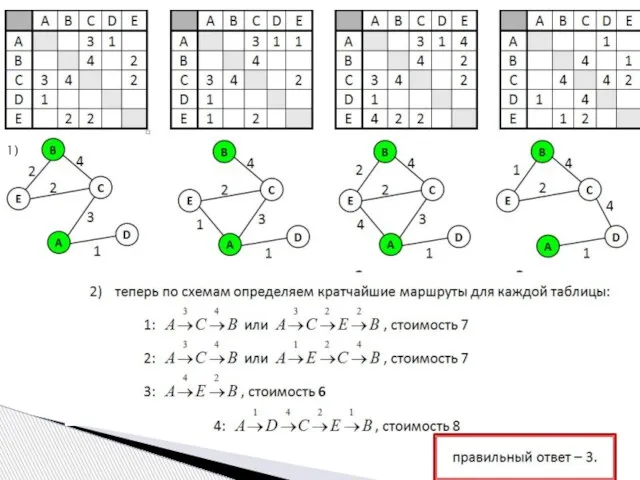
Задача
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

1)