Слайд 2План лекции
Модели информационного поиска
Булевская модель
Векторная модель
Вероятностная модель

Слайд 3План лекции
Модели информационного поиска
Булевская модель
Векторная модель
Вероятностная модель
Архитектура поисковой системы

Слайд 4План лекции
Модели информационного поиска
Булевская модель
Векторная модель
Вероятностная модель
Архитектура поисковой системы
PageRank

Слайд 5Модели информационного поиска
Что такое документ?
Что такое запрос?
При каком условии документ соответствует запросу?

Слайд 6Булевская модель
Словарь: T = {t1, . . . tn}
Документ: D ⊂ T,

иначе говоря D ∈ {0, 1}n
Запрос: t5 OR t7 NOT t12
Слайд 7Булевская модель
Словарь: T = {t1, . . . tn}
Документ: D ⊂ T,

иначе говоря D ∈ {0, 1}n
Запрос: t5 OR t7 NOT t12
Соответствие:
Формула запроса должна быть выполнена на документе.
Слайд 8Булевская модель
Словарь: T = {t1, . . . tn}
Документ: D ⊂ T,

иначе говоря D ∈ {0, 1}n
Запрос: t5 OR t7 NOT t12
Соответствие:
Формула запроса должна быть выполнена на документе.
Недостатки модели?
Слайд 9Векторная модель
Снова коллекция документов, каждый из которых теперь является мультимножеством слов.
Определим матрицу

M по формуле Mij = TFij · IDFi , где:
Частота терма TFij — относительная доля слова i в тексте j
Обратная встречаемость в документах IDFi — величина, обратная количеству документов, содержащих слово i
Слайд 10Векторная модель
Снова коллекция документов, каждый из которых теперь является мультимножеством слов.
Определим матрицу

M по формуле Mij = TFij · IDFi , где:
Частота терма TFij — относительная доля слова i в тексте j
Обратная встречаемость в документах IDFi — величина, обратная количеству документов, содержащих слово i
Физический смысл Mij — степень соответствия слова i тексту j
Слайд 11Векторная модель
Снова коллекция документов, каждый из которых теперь является мультимножеством слов.
Определим матрицу

M по формуле Mij = TFij · IDFi , где:
Частота терма TFij — относительная доля слова i в тексте j
Обратная встречаемость в документах IDFi — величина, обратная количеству документов, содержащих слово i
Физический смысл Mij — степень соответствия слова i тексту j
Запрос: t3 AND t5 (разрешаем только AND)
Слайд 12Релевантность в векторной модели
Запишем запрос в виде вектора:
Q = t3 AND t5

~ {0, 0, 1, 0, 1, 0, . . . , 0}
Мерой релевантности будет косинус между запросом и документом:
Слайд 13Вероятностная модель
для чайников
Документ: множество слов (булевский вектор) D = {d1, .

. . , dn}
Запрос: Qk — тоже, но храним как множество
Слайд 14Вероятностная модель
для чайников
Документ: множество слов (булевский вектор) D = {d1, .

. . , dn}
Запрос: Qk — тоже, но храним как множество
Соответствие:
Зафиксируем запрос Qk
Пусть есть распределение вероятностей на всех текстах “быть релевантным запросу Qk ”: обозначаем
Пусть есть распределение вероятностей на всех текстах “быть НЕрелевантным запросу Qk ”: обозначаем
Функцией соответствия будет их отношение (или логарифм этой дроби):
Слайд 15Вычисляем функцию соответствия
Воспользуемся теоремой Байеса ( )

Слайд 16Вычисляем функцию соответствия
Воспользуемся теоремой Байеса ( ):
Первый сомножитель одинаков для всех документов.

Слайд 17Вычисляем функцию соответствия
Воспользуемся теоремой Байеса ( ):
Первый сомножитель одинаков для всех документов.
Предполагая

независимость всех слов, второй сомножитель можно представить как произведение:
Слайд 18Вычисляем функцию соответствия II
Введем обозначения:
Предположим, что для каждого слова i , не

входящего в запрос,
Слайд 19Вычисляем функцию соответствия II
Введем обозначения:
Предположим, что для каждого слова i , не

входящего в запрос,
Теперь мы можем переписать нашу дробь:
Слайд 20Вычисляем функцию соответствия III

Слайд 21Вычисляем функцию соответствия III
Второй сомножитель одинаков для всех документов.
Забудем про него и

возьмем логарифм от первого:
Слайд 22Подбор параметров
Для использования полученной формулы нужно знать pik и qik .

Слайд 23Подбор параметров
Для использования полученной формулы нужно знать pik и qik .
Рецепт: пусть

у нас уже есть некий набор текстов, про которые мы знаем, релевантны они запросу Qk или нет. Тогда мы можем использовать формулы:
Слайд 24Подбор параметров II
Тут
f — общее число документов,
r — число релевантных

документов,
ri число релевантных документов, содержащих слово i ,
fi — общее число документов со словом i .
Слайд 25Архитектура поисковой системы
В каком формате запоминать интернет-страницы?
В какой структуре данных их хранить?
Как

обрабатывать запрос пользователя?
Слайд 26Анатомия поисковой системы
Любая поисковая система содержит три базовые части:
Робот (он же краулер,

спайдер или индексатор)
Базы данных
Клиент (обработка запросов)
Слайд 28Прямой и обратный индекс
Прямой индекс — записи отсортированы по
документам
Номер документа
Отсортированный список слов
Для

каждого слова: первые несколько вхождений, частота вхождений, формат вхождений
Обратный индекс — записи отсортированы по
словам
Номер слова
Отсортированный список документов
Для каждого документа: информация о вхождении
Слайд 29Релевантность
Наличие слов на сайте
Частота слов
Форматирование
Близость слов друг к другу
Количество ссылок с других

страниц на данную
Качество ссылок
Соответствие тематик сайта и запроса
Регистрация в каталоге, связанном с поисковой системой
Слайд 30Как работает клиент?
Разбирает запрос на слова
Переводит слова в их идентификаторы
Для каждого слова

находит в обратном индексе список документов, его содержащих
Одновременно бежит по этим спискам, ища общий документ
Для каждого найденного документа вычисляет степень релевантности
Сортирует образовавшийся список по релевантности
Слайд 31Качество поиска
Полнота: отношение количества найденных релевантных документов к общему количеству релевантных документов
Точность:

доля релевантных документов в общем количестве найденных документов
Benchmarks: показатели системы на контрольных запросах и специальных коллекциях документов
Оценка экспертов
Слайд 32PageRank
Как определить ссылочную популярность страницы (PageRank)?
Как быстро вычислить приближение PageRank?

Слайд 33PageRank: постановка задачи
Хотим для каждой страницы сосчитать показатель ее “качества”.
Идея [Брин, 1998]:

Определить рейтинг страницы через количество ведущих на нее ссылок и рейтинг ссылающихся страниц
Другие методы:
Учет частоты обновляемости страницы
Учет посещаемости
Учет регистрации в каталоге-спутнике поисковой системы
Слайд 34Модель случайного блуждания
Сеть:
Вершины
Ориентированные ребра (ссылки)
Передвижение пользователей по сети
Стартуем в случайной вершине
С вероятностью

ε переходим в случайную вершину
С вероятностью 1 − ε переходим по случайному исходящему ребру
Предельные вероятности
Для каждого k можно определить PRk (i) как
вероятность оказаться в вершине i через k шагов
limk→∞ PRk (i) = PR(i)
то есть для каждой вершины
есть предельная вероятность находится именно в ней
Слайд 35Основное уравнение PageRank
Пусть T1, . . . ,Tn — вершины, из которых

идут ребра в i , C(X) — обозначение для исходящей степени вершины X.
По определению PRk (i ) верно следующее:
Нужно перейти к пределу!
Практическое решение: вместо PR(i ) используют PR50(i ),
вычисленное по итеративной формуле.

























![Схема из [Brin,Page, 1998]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/418536/slide-26.jpg)








 Измельчительно-режущее оборудование
Измельчительно-режущее оборудование Комиссия по профориентационной работе
Комиссия по профориентационной работе Альберт Эйнштейн – личность века
Альберт Эйнштейн – личность века Тестовая игра Кокология
Тестовая игра Кокология Сбор нагрузок на 1м2 плиты перекрытия жилого здания
Сбор нагрузок на 1м2 плиты перекрытия жилого здания Урок литературного чтения И. А. Крылов Басня «Ворона и Лисица»
Урок литературного чтения И. А. Крылов Басня «Ворона и Лисица» Интерактивный учебник
Интерактивный учебник Modal verb must
Modal verb must Обзор продуктов Konica Minolta
Обзор продуктов Konica Minolta Обратный поток
Обратный поток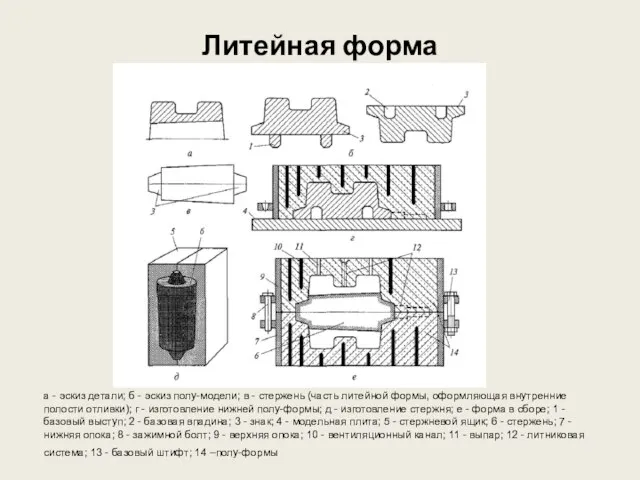 Литейная форма
Литейная форма Подбор сотрудника
Подбор сотрудника Технические средства телекоммуникационных технологий
Технические средства телекоммуникационных технологий Проектирование сварных и комбинированных заготовок
Проектирование сварных и комбинированных заготовок Конфликтологическая парадигма. Идеи Ч.Р.Миллса, Р.Дарендорфа, Л.Козера
Конфликтологическая парадигма. Идеи Ч.Р.Миллса, Р.Дарендорфа, Л.Козера Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006
Акварель Составлено доцентом кафедры изобразительного искусства СыктГУ Торлоповой Натальей Геннадьевной 2006 Русская юзабилити в изгнании
Русская юзабилити в изгнании АРТЕРИАЛЬНАЯ ГИПОТОНИЯ
АРТЕРИАЛЬНАЯ ГИПОТОНИЯ Земельный участокв Ставропольском районе Самарской области
Земельный участокв Ставропольском районе Самарской области ?
? Городской конкурс Читатель года
Городской конкурс Читатель года У.У. Сойер
У.У. Сойер Презентация на тему Деревья леса
Презентация на тему Деревья леса История возникновения шахмат
История возникновения шахмат Инфракрасное и ультрафиолетовое излучения
Инфракрасное и ультрафиолетовое излучения ПРИМЕНЕНИЕ ПРОЕКТНОЙ ТЕХНОЛОГИИ В РАБОТЕ С ОДАРЕННЫМИ ДЕТЬМИ
ПРИМЕНЕНИЕ ПРОЕКТНОЙ ТЕХНОЛОГИИ В РАБОТЕ С ОДАРЕННЫМИ ДЕТЬМИ Гусеничный пандус
Гусеничный пандус Сила достижения
Сила достижения