Интерференция света

Принцип Гюйгенса
Волновая теория света основана на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн даёт положение волнового фронта в последующий момент времени
На основе волновой теории удалось правильно объяснить законы отражения и преломления света

Интерференция
При соблюдении некоторых условий наблюдается отклонение от закона независимости световых пучков. Действие, производимое несколькими световыми лучами отличается от суммы воздействий всех лучей. Такое явление называется интерференцией
При интерференции происходит увеличение средней интенсивности света в одних областях и уменьшение в других

Интерференция света (от лат. inter – взаимно, между собой и ferio – ударяю, поражаю) – пространственное перераспределение энергии света при наложении двух или нескольких световых волн.
Интерференция волн – одно из основных свойств волн любой природы (упругих, электромагнитных, в т.ч. световых и др.). Такие характерные волновые явления, как излучение, распространение и дифракция, тоже связаны с интерференцией. Интерференцией света объясняются окраска тонких масляных пленок на поверхности воды, металлический отлив в окраске крыльев насекомых и птиц, появление цветов побежалости на поверхности металлов, голубоватый цвет просветленных линз оптических приборов и пр.
Некоторые явления интерференции света исследовались еще И. Ньютоном в XVII в., но не могли быть им объяснены с точки зрения его корпускулярной теории. Правильное объяснение интерференции света как типично волнового явления было дано в начале XIX в. Т. Юнгом и О. Френелем.

Когерентность и монохроматичность
Необходимыми условиями возникновения интерференции являются монохроматичность и когерентность световых потоков
Монохроматичность световых волн означает неизменность во времени их длин и частот колебаний
Любой световой поток можно представить как суперпозицию монохроматичных волн

Когерентность и монохроматичность
Интерферировать между собой могут только монохроматические составляющие нескольких световых потоков. При этом суммарная интерференционная картина является наложением всех монохроматических интерференционных картин

Когерентность и монохроматичность
Строго монохроматическое излучение получить невозможно
При излучении света одной длины волны источником, происходит случайное изменение фазы колебаний, это приводит к случайным быстрым изменениям интерференционной картины. Инерционный фоточувствительный прибор при этом не успевает регистрировать её

Когерентность и монохроматичность
Стабильную интерференционную картину можно получить используя когерентные источники
Когерентность источников излучения означает, что колебательные процессы протекают в них согласованно во времени

Когерентность и монохроматичность
Когерентное излучение можно получить двумя способами
От нескольких независимых источников света высокой степени монохроматичности (лазеров)
Выделяя лучи от одного и того же источника
Второй способ получил наибольшее распространение

Пусть в точку А одновременно поступает монохроматическое плоскополяризованное излучение от двух источников света S1 и S2. Если векторы напряженности электрических полей этих волн Е1 и E2 имеют в точке А одинаковое направление, то в этой точке А суммарная напряженность поля E = E1+E2.
Энергия в единице объема, подсчитанная по суммарной напряженности Е:
оказывается больше суммы энергий, подсчитанных по напряженностям E1 и E2.

Рассмотрим простейший случай интерференции монохроматических световых волн от двух одинаковых источников, которые стали излучать одновременно, поэтому фазы векторов Е1 и Е2 зависят только от расстояний х1 и х2
т.к.

В точках, где аргумент косинуса равен нечетному числу π/2, соsω(x2-x1)/2c = 0, суммарная напряженность электрического поля Е в любой момент времени равна нулю, и световые волны взаимно «гасятся».
Подставляя ω = 2π/Т = 2πс/λ, можно найти расположение тех точек, в которых происходит взаимное «гашение» двух монохроматических световых волн (с одинаковой амплитудой E0):
В точках, отстоящих от источников света S1 и S2 на расстояниях, удовлетворяющих условию, света не будет.

Волновые свойства света наиболее отчетливо обнаруживают себя в интерференции и дифракции.
Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:

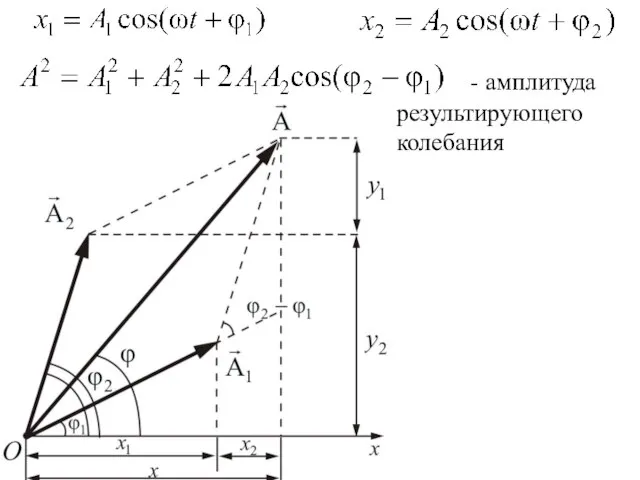
- амплитуда результирующего колебания

Если разность фаз колебаний возбужденных волнами в некоторой точке пространства остается постоянной во времени, то такие волны называются когерентными.
В случае некогерентных волн разность фаз
непрерывно изменяется.

В случае когерентных волн
(7.2.2)
Последнее слагаемое в этом выражении
-интерференционный член.
,
; в минимуме
, интенсивность
где
; в максимуме
Интенсивность световой волны J равна квадрату амплитуды А. Тогда суммарная интенсивность:

Для некогерентных источников интенсивность результирующей волны всюду одинакова и, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:
Некогерентность естественных источников света обусловлена тем, что излучение тела слагается из волн, хаотически испускаемых многими атомами.
Фазы каждого цуга волны, испускаемого отдельным атомом никак не связаны друг с другом. Атомы излучают хаотически.

Периодическая последовательность горбов и впадин волны и образующиеся в процессе акта излучения одного атома, называется цугом волн или волновым цугом.
Процесс излучения одного цуга атома длится
Длина цуга
В одном цуге укладывается примерно
длин волн.

Рисунок 7.3
Первая волна
Разность фаз двух когерентных волн -
Оптическая разность хода -
L – оптическая длина пути; s – геометрическая длина
пути; n – показатель преломления среды.
вторая
Рассмотрим интерференцию двух когерентных волн:

Условие максимума и минимума интерференции:
Если оптическая разность хода равна целому числу длин волн
(7.2.3)
- условие интерференционного максимума.
Если оптическая разность хода равна полу-целому числу длин волн
(7.2.4)
- условие интерференционного минимума.

Расстояние между двумя соседними
максимумами (или минимумами) равно
Максимумы интенсивности будут наблюдаться в координатах:
(m = 0, 1, 2, …),
а минимумы – в координатах:
- ширина интерференционной полосы.
Измерив
, зная l и d, можно вычислить длину волны λ. Именно так вычисляют длины волн разных цветов в спектроскопии.

Световые волны одинаковой длины волны, которые приходят в данную точку с постоянной (не изменяющейся со временем) разностью фаз, называются когерентными. Когерентные волны дают неизменную со временем интерференционную картину (распределение интенсивности света в пространстве или на экране.
Область пространства, в которой амплитуда результирующей волны усиливается, называется областью конструктивной интерференции, а в которой ослабляется – деструктивной.

Когерентность и монохроматичность
Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Этому условию удовлетворяют монохроматические волны – волны одной определенной и строго постоянной частоты.

Волну можно приближенно считать монохроматической только в течение времени
(7.4.1)
где
– время когерентности
За промежуток времени
разность фаз колебаний
изменится на π.
Время когерентности – время, по истечению которого разность фаз волны в некоторой, но одной и той же точке пространства, изменяется на π.

Когерентность колебаний которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временнóй когерентностью.

Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно-когерентными.
Радиусом когерентности (или длиной пространственной когерентности) называется максимальное, поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции.
Пространственная когерентность
ρк – радиус пространственной когерентности;
λ – длина волны;
θ – угловой размер источника.

Условия пространственной когерентности двух волн
1) постоянная во времени разность фаз:
ω1t +φ01 – ω2 t – φ02 = const,
откуда следует
(ω1 – ω2)t + φ01 – φ02 = const.
Это справедливо лишь при
ω1 = ω2
Таким образом, условие постоянства во времени разности фаз эквивалентно условиям одинаковости для когерентных лучей циклических частот в вакууме.
2) соизмеримость амплитуд интерферирующих волн,
3) одинаковое состояние поляризации,
4) лучи, пройдя разные пути, встречаются в некоторой точке пространства.

Интерференция в тонких пленках
Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта.

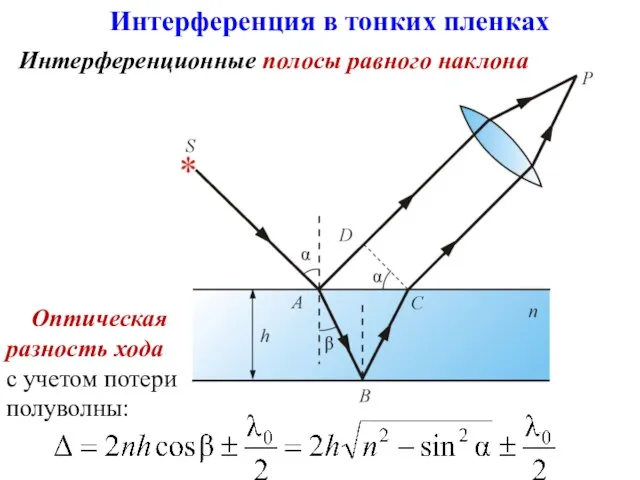
Интерференционные полосы равного наклона
Интерференция в тонких пленках
Оптическая
разность хода
с учетом потери
полуволны:

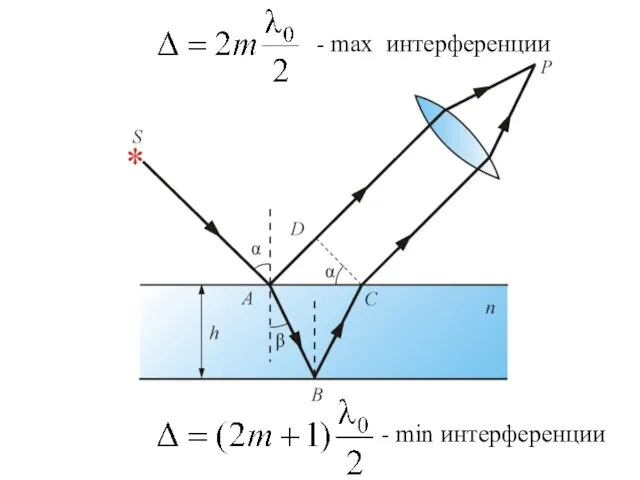
- max интерференции
- min интерференции

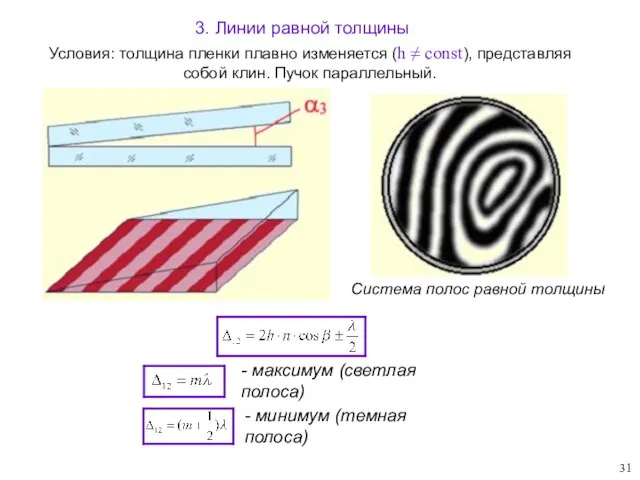
3. Линии равной толщины
Условия: толщина пленки плавно изменяется (h ≠ const), представляя собой клин. Пучок параллельный.
Система полос равной толщины
- максимум (светлая полоса)
- минимум (темная полоса)

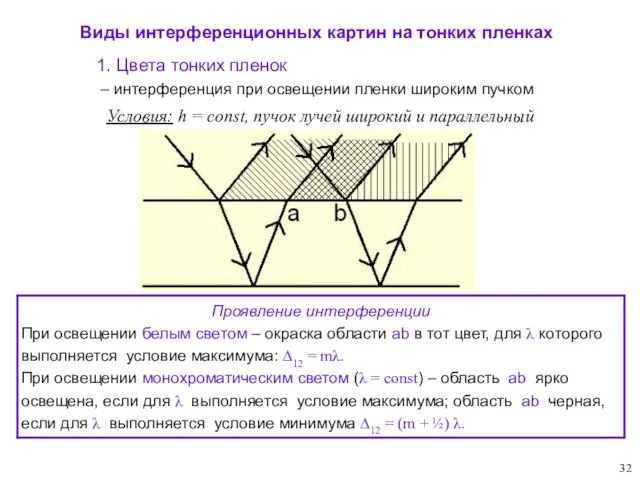
Виды интерференционных картин на тонких пленках
Условия: h = const, пучок лучей широкий и параллельный
1. Цвета тонких пленок
– интерференция при освещении пленки широким пучком

Интерференция от клина.
Полосы равной толщины
В белом свете интерференционные полосы, при отражении от тонких пленок - окрашены. Поэтому такое явление называют цвета тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.

Опыты с мыльной пленкой

Изменение картины интерференции по мере уменьшения толщины мыльной пленки

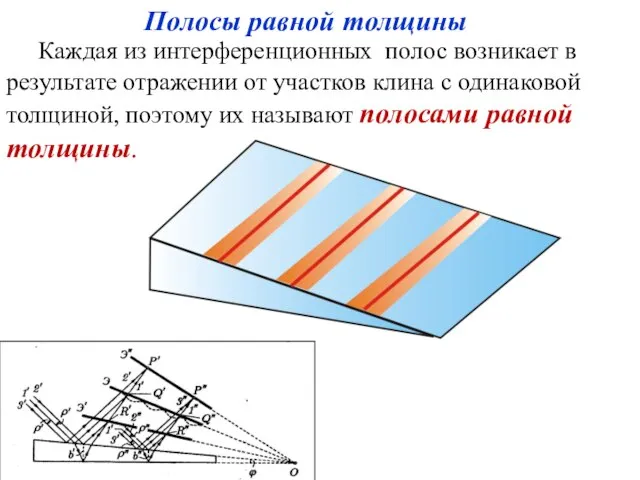
Каждая из интерференционных полос возникает в результате отражении от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
Рис. 7.15
Полосы равной толщины

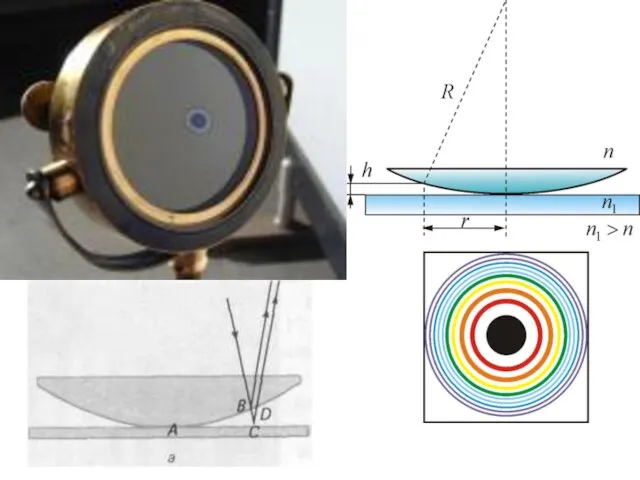
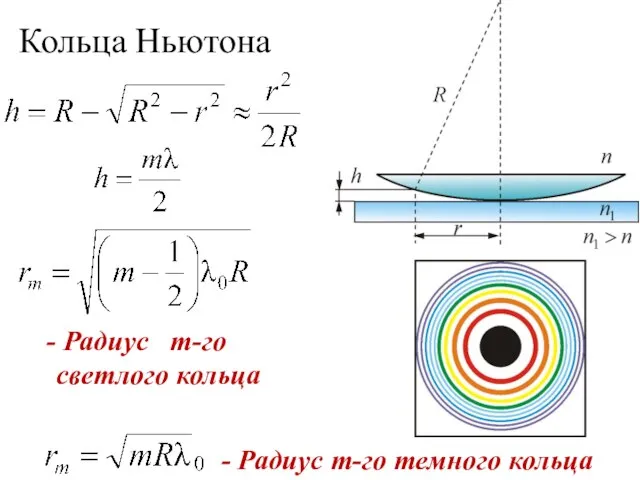
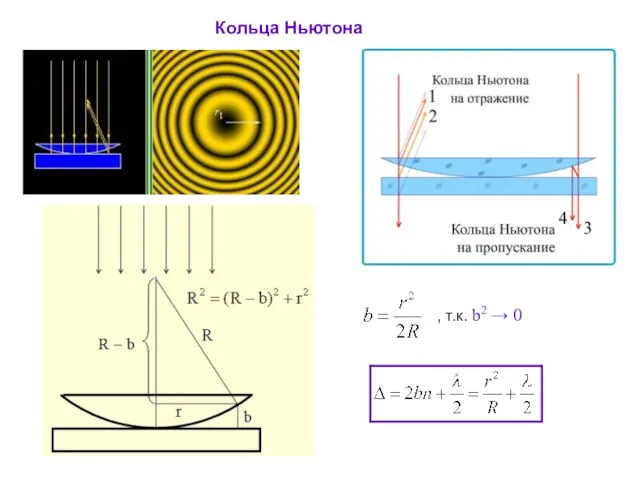
Кольца Ньютона
Ньютон объяснил это явление на основе корпускулярной теории света.
Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре
между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.

Кольца Ньютона
- Радиус m-го темного кольца
Радиус m-го
светлого кольца

Кольца Ньютона
, т.к. b2 → 0

Условие максимума (светлые кольца) ∆ = m λ, где m – целое число.
- радиус m-го светлого кольца в отраженном свете
(и темного – в прошедшем)
Условие минимума (темные кольца) ∆ = (m + ½) λ.
- радиус m-го темного кольца в отраженном свете
(и светлого – в прошедшем)
Кольца Ньютона в зеленом и красном свете
Пример применения – проверка качества шлифовки линз.

Использование интерференции
Явление интерференции нашло широкое практическое применение
Создание просветлённых покрытий
Измерение малых расстояний и перемещений
Контроль поверхности
Измерение показателя преломления
Голография

Применение интерференции света
1. Тот факт, что расположение интерференционных полос зависит от длины волны и разности хода лучей, позволяет по виду интерференционной картины (или их смещению) проводить точные измерения расстояний при известной длине волны или, наоборот, определять спектр интерферирующих волн (интерференционная спектроскопия).

2. По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной.

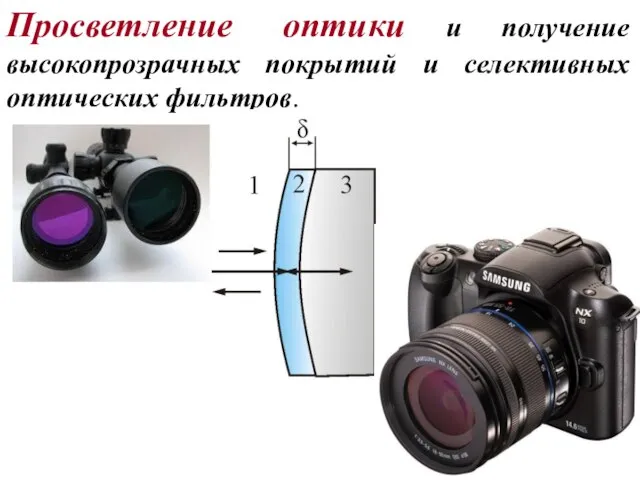
Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров.

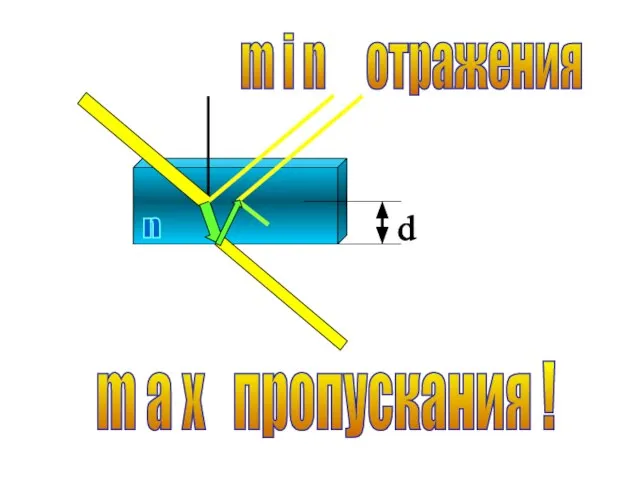
m i n отражения
m a x пропускания !

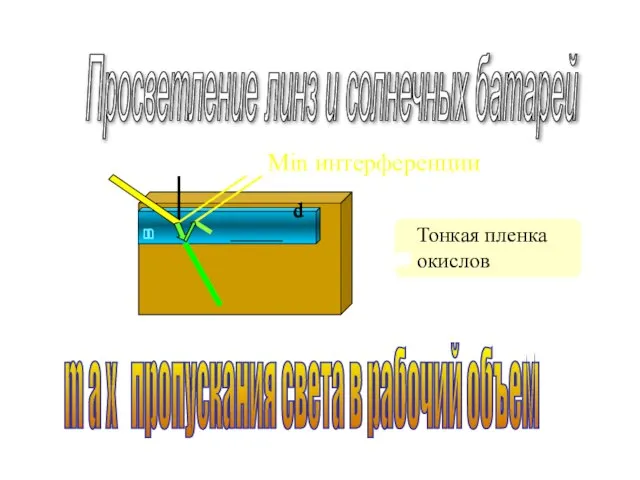
m a x пропускания света в рабочий объем
Просветление линз и солнечных батарей
Min интерференции

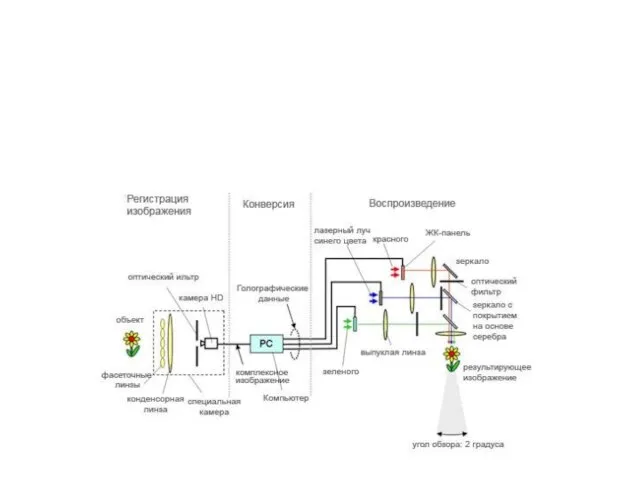
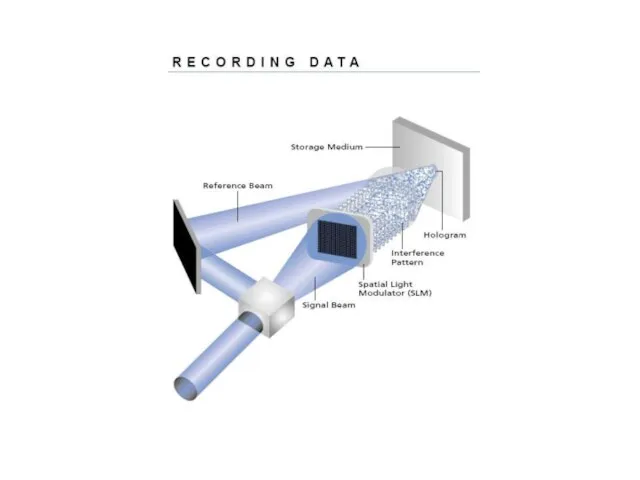
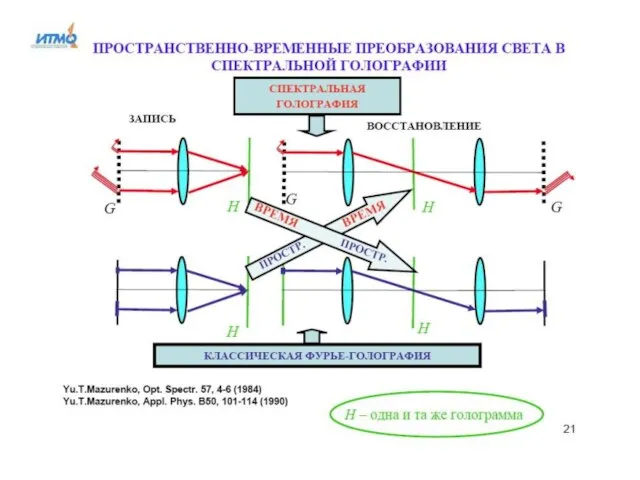
Голография
Записанные на голограмме световые волны при их восстановлении создают полную иллюзию существования объекта, неотличимого от оригинала. В пределах телесного угла, охватываемого голограммой, изображение объекта можно осматривать с разных направлений, то есть оно является трехмерным. Эти свойства голографии используются в лекционных демонстрациях, при создании объемных копий произведений искусства, голографических портретов (изобразительная голография).
Голография – это способ, который позволяет регистрировать (записывать) волновой фронт, отраженный от предмета, а затем восстанавливать его таким образом, что у наблюдателя возникает полное ощущение, будто он действительно видит реальный предмет. Подобный эффект обусловлен тем, что голографическое изображение получается трехмерным в той же мере, как и реальный предмет.

Принципы голографии впервые были изложены английским ученым Денишом Габором в 1948 году. В то время важность этого открытия еще не была вполне очевидной, и лишь очень немногие исследователи, работавшие в 50-е годы в данной области, страдали от отсутствия подходящего источника света, который обладал бы весьма важным свойством – когерентностью.
За это изобретение он получил в 1971 году Нобелевскую премию по физике.
В 1960 году был изготовлен первый лазер. Этот прибор создает свет достаточной когерентности, и американские ученые Иммет Лейт и Юрис Упатниекс смогли использовать его для получения первых голограмм, создававших изображения предметов во всех трех измерениях. Исследования продолжались в последующие годы, и с тех пор на тему голографии были опубликованы сотни научных статей и издано много книг

Две фотографии одной голограммы, сделанные с разных ракурсов
Голограмма на батарее мобильного телефона. Наносится в качестве знака защиты от подделок.

Плоский характер изображения при обычной фотографии обусловлен тем, что на фотопластинке фиксируется только относительная интенсивность световых волн, отраженных от различных точек предмета, без учета фазовых соотношений между этими волнами, которые обусловлены различным расстоянием точек предмета от фотопластинки.
Двулучевая голография. Расширенной линзой пучок света делится на 2 части: одна часть (опорный пучок) падает на зеркало и отражается к фотопластинке. Вторая часть (предметный пучок) падает на предмет, отражается от него и падает на фотопластинку. Опорный и предметный пучки интерферируют и эта картина фиксируется фотопластинкой. В пластинке запечатлена полная структура волны, отраженной от предмета с сохранениями как фазовых состояний, так и относительной интенсивности.
Для восстановления изображения проявленную фотопластинку помещают в то самое положение, в котором она находилась при фотографировании и освещают опорным пучком (предметный пучок перекрывают). Опорный пучок, дифрагирует на голограмме и создается волна, имеющая точно такую же структуру, как волна, отражавшаясяпредметом

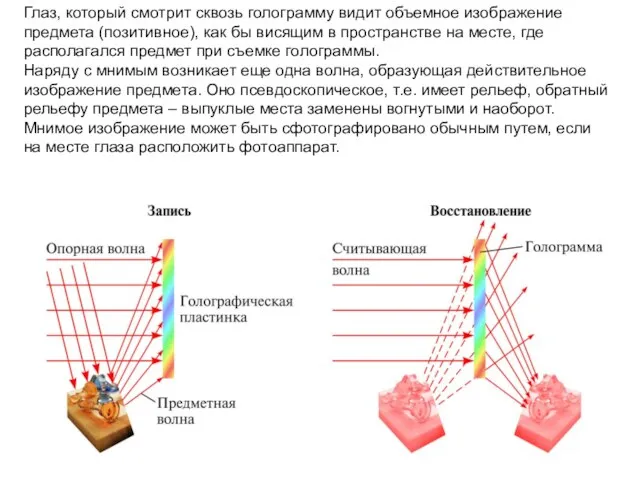
Глаз, который смотрит сквозь голограмму видит объемное изображение предмета (позитивное), как бы висящим в пространстве на месте, где располагался предмет при съемке голограммы.
Наряду с мнимым возникает еще одна волна, образующая действительное изображение предмета. Оно псевдоскопическое, т.е. имеет рельеф, обратный рельефу предмета – выпуклые места заменены вогнутыми и наоборот. Мнимое изображение может быть сфотографировано обычным путем, если на месте глаза расположить фотоаппарат.