Исполнитель калькулятор

Алгоритмы
Свойства алгоритма
дискретность: состоит из отдельных шагов (команд)
понятность: должен включать только команды, известные исполнителю (входящие в СКИ)
определенность: при одинаковых исходных данных всегда выдает один и тот же результат
конечность: заканчивается за конечное число шагов
массовость: может применяться многократно при различных исходных данных
корректность: дает верное решение при любых допустимых исходных данных
Алгоритм – это четко определенный план действий для исполнителя.

Система команд
Исполнитель Калькулятор работает с одним числом и умеет выполнять с ним две операции (команды):
1. прибавь 2
2. умножь на 3
Программа – это последовательность номеров команд, которые нужно выполнить.
Программа 12211
2
начальное число
4
12
36
38
40
1
2
2
1
1
результат

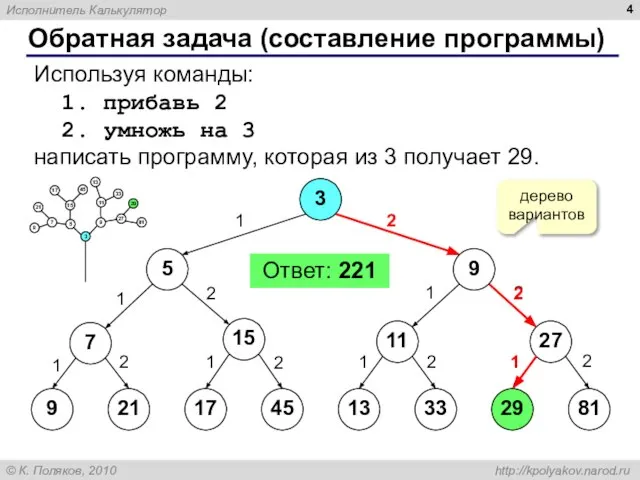
Обратная задача (составление программы)
Используя команды:
1. прибавь 2
2. умножь на 3
написать программу, которая из 3 получает 29.
Ответ: 221
3
5
29
1
дерево вариантов
9
7
15
11
27
9
21
17
45
13
33
81
2
1
1
1
1
1
2
2
2
2
2
2
2
1
2
1

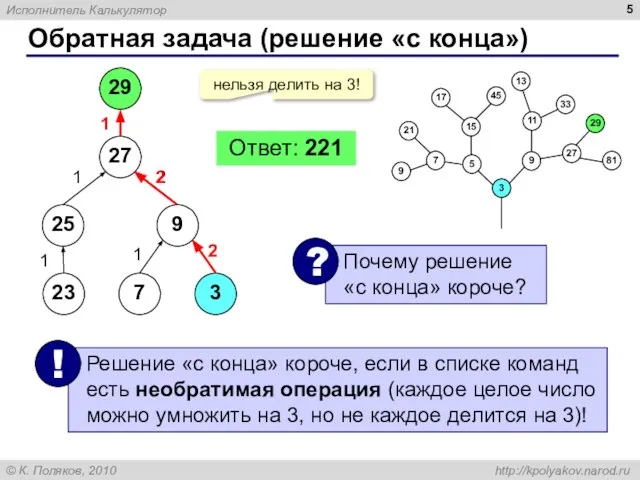
Обратная задача (решение «с конца»)
29
нельзя делить на 3!
27
25
9
23
7
3
1
1
1
2
2
2
2
1
Ответ: 221

Ещё пример
Используя команды:
1. прибавь 2
2. умножь на 3
написать программу, которая из 2 получает 15.

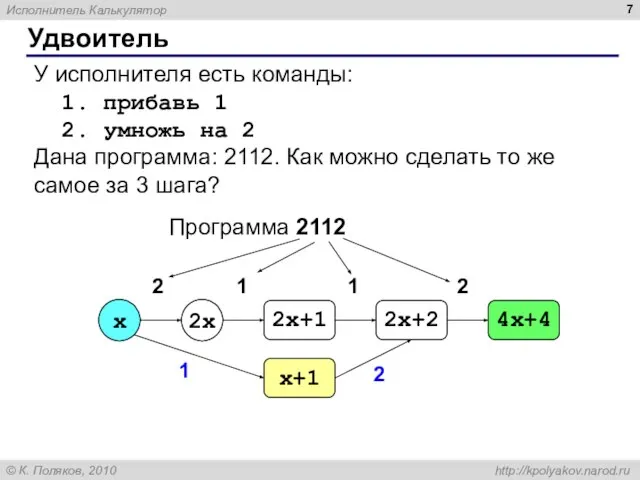
Удвоитель
У исполнителя есть команды:
1. прибавь 1
2. умножь на 2
Дана программа: 2112. Как можно сделать то же самое за 3 шага?
Программа 2112
x
2x
2
1
1
2
2x+1
2x+2
4x+4
x+1
1
2

Удвоитель
У исполнителя есть команды:
1. прибавь 1
2. умножь на 2
Задания:
Какие числа можно получить из 0?
Как из числа 5 получить 105?
Какие числа можно получить из отрицательного числа N?
Как построить самую короткую программу для получения заданного X из 0?
Найдите минимальное число, которое может быть получено из 0 только за 6 шагов.

Удвоитель
У исполнителя есть команды:
1. прибавь 1
2. умножь на 2
Докажите, что:
любое число, меньшее 10, можно получить из 0 за 5 шагов
любое число, меньшее 100, можно получить из 0 за 12 шагов

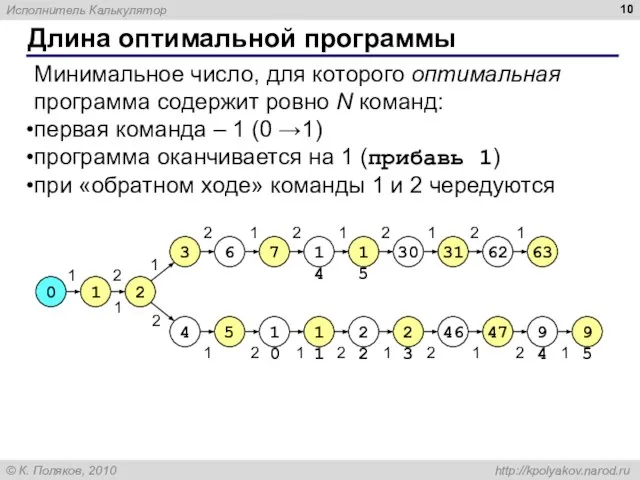
Длина оптимальной программы
0
Минимальное число, для которого оптимальная программа содержит ровно N команд:
первая команда – 1 (0 →1)
программа оканчивается на 1 (прибавь 1)
при «обратном ходе» команды 1 и 2 чередуются

Раздвоитель
У исполнителя есть команды:
1. вычти 1
2. раздели на 2
Задания:
Какие числа можно получить из положительного числа N?
Какие числа можно получить из отрицательного числа N?
Как быстрее всего получить 0 из положительного числа N?

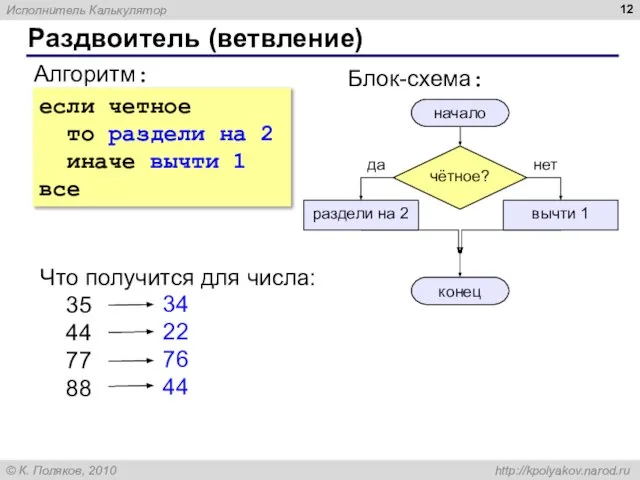
Раздвоитель (ветвление)
Алгоритм:
начало
конец
раздели на 2
вычти 1
Блок-схема:
Что получится для числа:
35
44
77
88
34
22
76
44
да
нет
если четное
то раздели на 2
иначе вычти 1
все

Раздвоитель (циклы)
Алгоритм:
Что получится:
10
20
30
50
60
0
1
3
3
6
Цикл – это повторение одинаковых действий.
нц 5 раз
если четное
то раздели на 2
иначе вычти 1
всё
кц
если четное
то раздели на 2
иначе вычти 1
всё
конец цикла
тело цикла
начало цикла

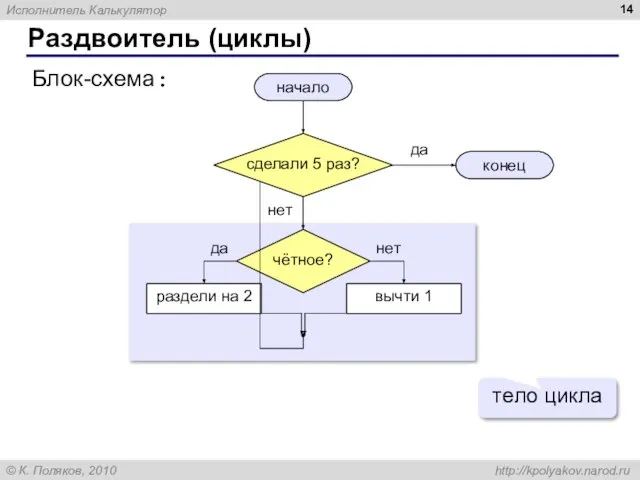
Раздвоитель (циклы)
начало
конец
раздели на 2
вычти 1
Блок-схема:
да
нет
да
нет
тело цикла

нц пока положительное
если четное
то раздели на 2
иначе вычти 1
всё
кц
Раздвоитель (циклы)
Алгоритм:
Задание: нарисуйте блок-схему.
Сколько шагов цикла выполнится для числа
15
16
128
7
5
8

нц пока положительное
нц пока четное
раздели на 2
кц вычти 1
кц
Раздвоитель (циклы)
Алгоритм получения 0 из положительного числа:
Задание: нарисуйте блок-схему.

нц пока положительное
вычти 1
нц пока четное
раздели на 2 кц
кц
Раздвоитель (циклы)
Алгоритм получения 0 из положительного числа:
Задание: нарисуйте блок-схему.

нц пока положительное
если нечетное
то вычти 1
всё
нц пока четное раздели на 2
кц
кц
Раздвоитель (циклы)
Алгоритм получения 0 из положительного числа:
Задание: нарисуйте блок-схему.

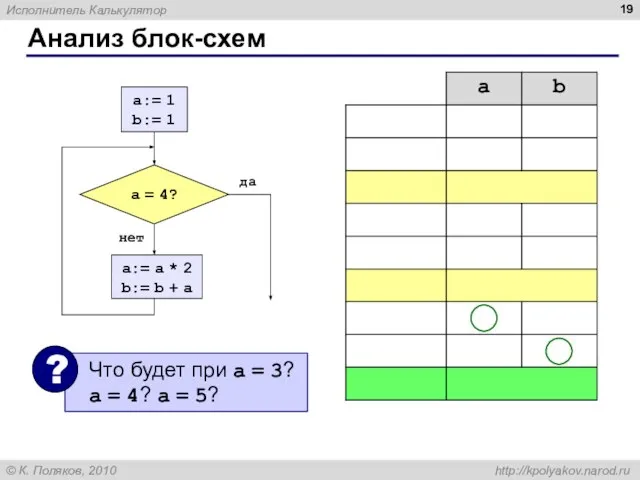
Анализ блок-схем

Анализ блок-схем
Напишите программу, в которой a, b и c вводятся с клавиатуры. Заполните таблицу:
вывод "a=", a, "b=", b
вывод a, b
вывод a, " ", b

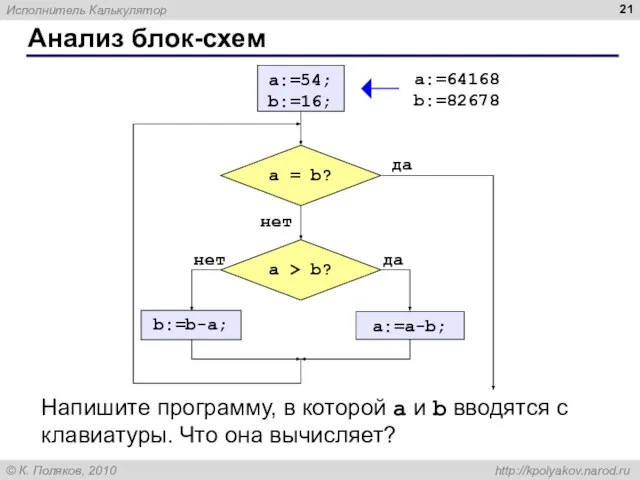
Анализ блок-схем
Напишите программу, в которой a и b вводятся с клавиатуры. Что она вычисляет?
a:=64168
b:=82678

Алгоритм Евклида
Евклид
(365-300 до. н. э.)
НОД(a,b)= НОД(a-b, b)
= НОД(a, b-a)
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.
НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7)
НОД (1998, 2) = НОД (1996, 2) = … = 2
Пример:
много шагов при большой разнице чисел:
= НОД (7, 7) = 7
Надо: вычислить наибольший общий делитель (НОД) чисел a и b.

Модифицированный алгоритм Евклида
НОД(a,b)= НОД(mod(a,b), b)
= НОД(a, mod(b,a))
Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД.
НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7
Пример:

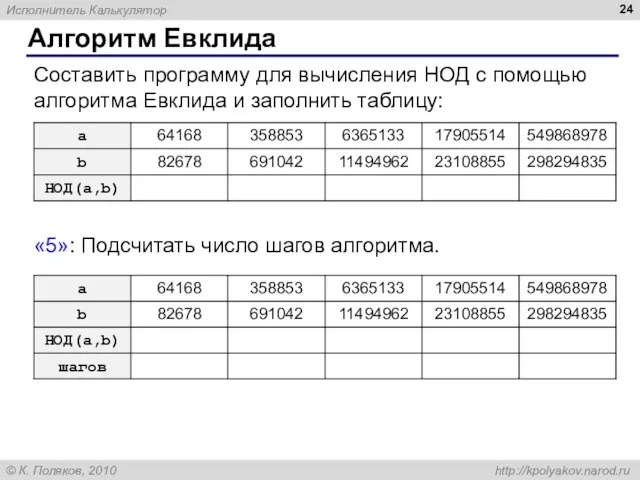
Алгоритм Евклида
Составить программу для вычисления НОД с помощью алгоритма Евклида и заполнить таблицу:
«5»: Подсчитать число шагов алгоритма.