Решение задач оптимизации в Excel

Для решения задач оптимизации необходимо:
Задать целевую функцию
Создать математическую модель задачи
Решить задачу на компьютере

Математическая модель
Математическая модель – это приближенное описание какого-либо класса явлений средствами математической символики.
При составлении математической модели решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи.
В любую математическую модель входят две составляющие:
Ограничения, которые устанавливают зависимости между переменными.
Граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Задача
Компания производит полки для ванных комнат двух типов - А и В. Агенты по продаже считают, что неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 час. в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл., то сколько полок надо выпускать в неделю, чтобы получить максимальную прибыль?

Целевая функция
Очевидно, что в качестве критерия оптимизации в данном случае выступает функция прибыли. Оптимальным будет считаться тот из вариантов решения, в котором значение прибыли будет максимальным. Учитывая, что «…прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл.…» целевая функция будет выглядеть следующим образом:
3x1 + 4x2 ⇒ max, где
x1 – объем производства полок типа A
x2 – объем производства полок типа B

Ограничение на объем производства:
«…Агенты по продаже считают, что неделю на рынке может быть реализовано до 550 полок…» Очевидно, что совокупный объем производства полок не должен превышать 550 единиц, или, в математическом виде:
x1 + x2 ≤ 550

Ограничение на использование оборудования:
«…Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 часов в неделю…» На основе этой информации можно сделать вывод, что общее время использования оборудования в рамках данного проекта не должно превышать 160 часов в неделю. Переведя время, необходимое для изготовления одной полки в часы (с целью сопоставимости единиц измерения правой и левой части неравенства) получим:
0,2x1 + 0,5x2 ≤ 160

Ограничение на использование материалов:
«…Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю…» На основе этой информации можно сделать вывод, что общее количество материала, затрачиваемого для реализации данного проекта не должно превышать 120 м2:
2x1 + 3x2 ≤ 120

Граничные условия
В качестве граничных условий в данном примере могут быть использованы следующие утверждения, вытекающие из сути поставленной задачи:
Объем производства полок типа А и полок типа В – неотрицательное значение.
Объем производства полок типа А и полок типа В – целое число.
x1, x2 ≥ 0
x1, x2 – целое

Ввод условий задачи
Ввод условий задачи состоит из следующих основных шагов:
Создание формы для ввода данных, необходимых для последующего решения.
Ввод исходных данных и зависимостей из математической модели.
Указание целевой ячейки (ячейки, в которую введена целевая функция), ввод ограничений и граничных условий в диалоговом окне Поиск решения.

Создание формы для ввода данных
Такая форма должна содержать возможность ввода всех данных, необходимых для решения поставленной задачи:
искомых переменных;
целевой функции;
правой и левой части неравенств, описывающих ограничения, налагаемые на возможные варианты решения поставленной задачи.

Ввод исходных данных
Отметим, что целевая функция и левые части неравенств, определяющих возможные варианты решения поставленной задачи, вводятся формулой, в которой роль искомых переменных играют адреса ячеек, зарезервированных для вывода их значений после решения задачи, а роль коэффициентов – адреса ячеек, содержащих соответственные коэффициенты.

Назначение целевой функции, ввод ограничений и граничных условий
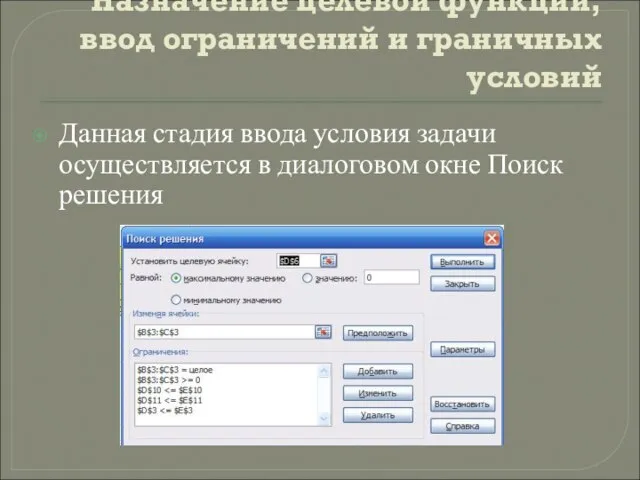
Данная стадия ввода условия задачи осуществляется в диалоговом окне Поиск решения

Назначить целевую ячейку
Для этого в поле «Установить целевую ячейку:» вводится адрес ячейки, содержащей целевую функцию. Затем устанавливается направление последней – значение, к которому она должна стремиться исходя из условий задачи (минимальное, максимальное, конкретное, задаваемое пользователем).
В поле «Изменяя ячейки:» ввести адреса ячеек, зарезервированных для искомых переменных.

Ввести ограничения и граничные условия
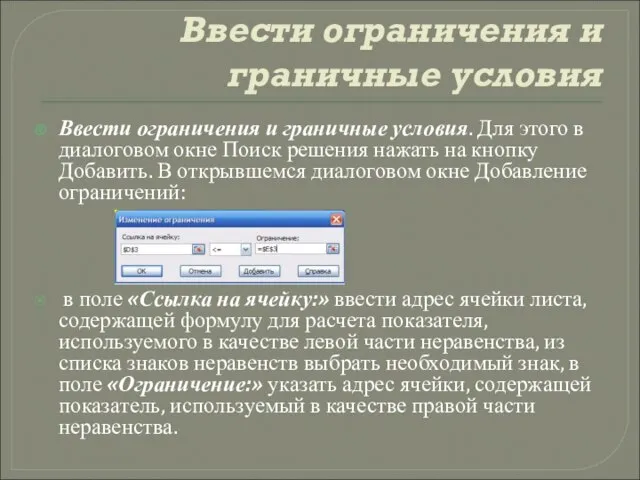
Ввести ограничения и граничные условия. Для этого в диалоговом окне Поиск решения нажать на кнопку Добавить. В открывшемся диалоговом окне Добавление ограничений:
в поле «Ссылка на ячейку:» ввести адрес ячейки листа, содержащей формулу для расчета показателя, используемого в качестве левой части неравенства, из списка знаков неравенств выбрать необходимый знак, в поле «Ограничение:» указать адрес ячейки, содержащей показатель, используемый в качестве правой части неравенства.

Получение результата
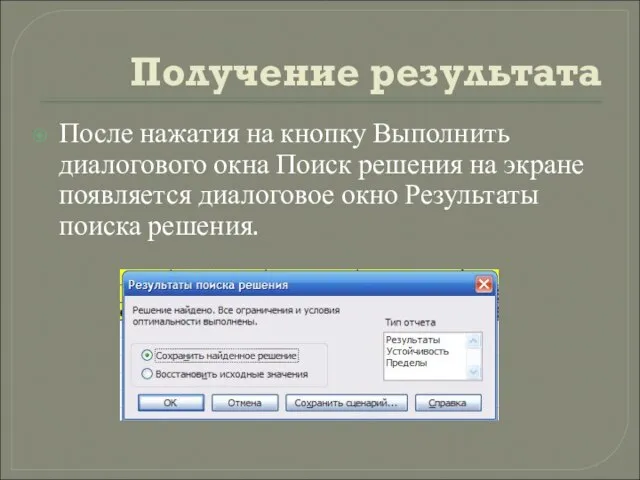
После нажатия на кнопку Выполнить диалогового окна Поиск решения на экране появляется диалоговое окно Результаты поиска решения.

Решение найдено