Исследование функции и ее свойства

.
Цель работы
Изучить:
- понятие функции;
- виды функций;
- способы задания функций;
- свойства функций;

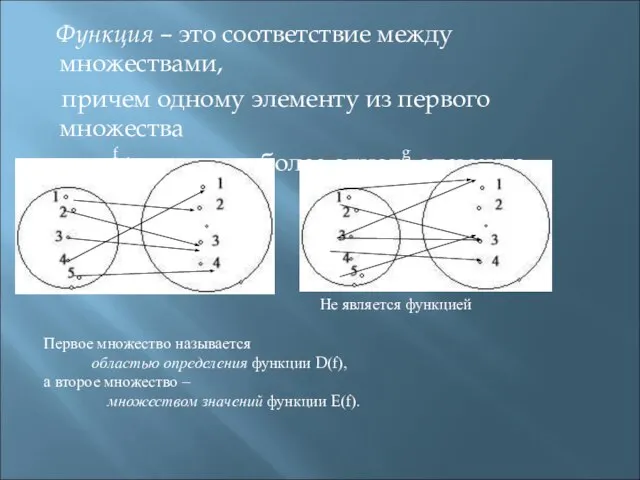
Функция – это соответствие между множествами,
причем одному элементу из первого множества
соответствует не более одного элемента второго
множества
Первое множество называется
областью определения функции D(f),
а второе множество –
множеством значений функции E(f).
f
g
Не является функцией
f

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)
Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)

Виды функций
Линейная
Прямая пропорциональность
Обратная пропорциональность
Квадратичная
Кубическая
Квадратный корень
Модуль

Линейная функция.
Линейная функция- функция, которая задана формулой y=kx+b, где k и b-действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
Область определения- множество всех действительных чисел
Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая.
0
У=2х+1

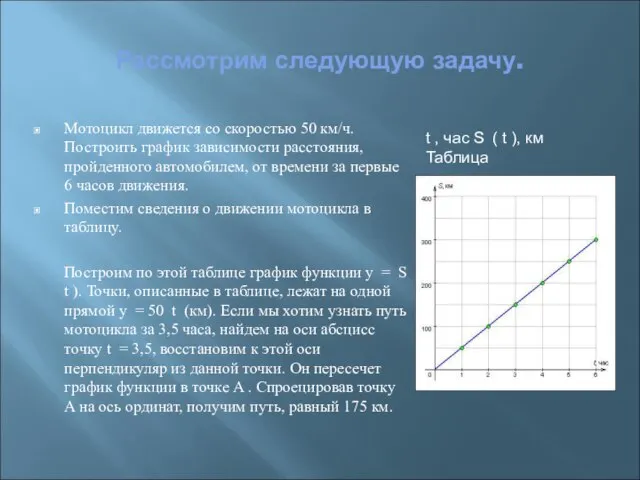
Рассмотрим следующую задачу.
Мотоцикл движется со скоростью 50 км/ч. Построить график зависимости расстояния, пройденного автомобилем, от времени за первые 6 часов движения.
Поместим сведения о движении мотоцикла в таблицу.
Построим по этой таблице график функции y = S ( t ). Точки, описанные в таблице, лежат на одной прямой y = 50 t (км). Если мы хотим узнать путь мотоцикла за 3,5 часа, найдем на оси абсцисс точку t = 3,5, восстановим к этой оси перпендикуляр из данной точки. Он пересечет график функции в точке A . Спроецировав точку A на ось ординат, получим путь, равный 175 км.
t , час S ( t ), км Таблица

Прямая пропорциональность.
Прямая пропорциональность- функция, заданная формулой у=kx. Число k называется коэффициентом пропорциональности.
Свойства функции y=kx:
Область определения функции- множество всех действительных чисел
y=kx - нечетная функция
При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком является прямая, проходящая через (0;0)
У=3х

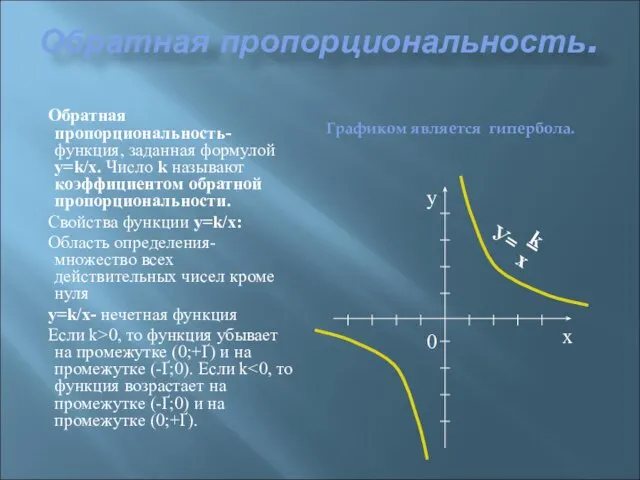
Обратная пропорциональность.
Обратная пропорциональность- функция, заданная формулой y=k/х. Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
Область определения- множество всех действительных чисел кроме нуля
y=k/x- нечетная функция
Если k>0, то функция убывает на промежутке (0;+Ґ) и на промежутке (-Ґ;0). Если k<0, то функция возрастает на промежутке (-Ґ;0) и на промежутке (0;+Ґ).
Графиком является гипербола.

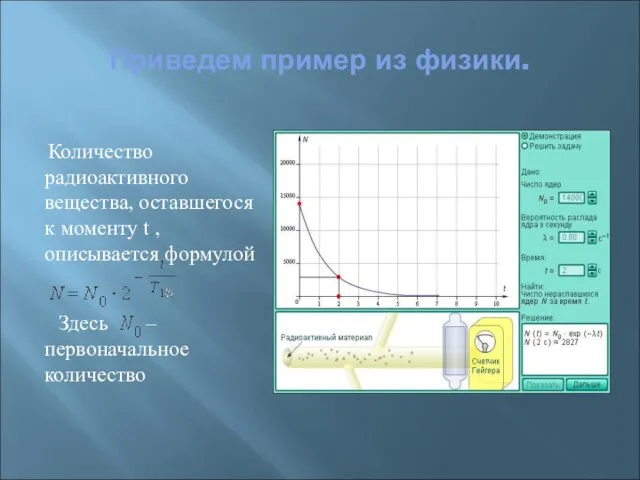
Приведем пример из физики.
Количество радиоактивного вещества, оставшегося к моменту t , описывается формулой
Здесь – первоначальное количество

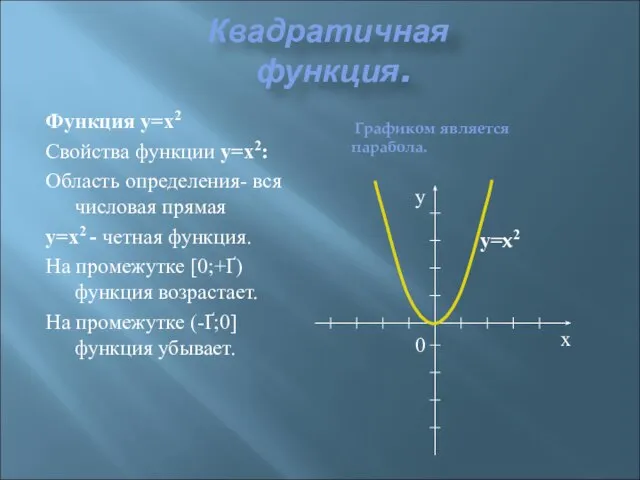
Квадратичная
функция.
Функция y=x2
Свойства функции y=x2:
Область определения- вся числовая прямая
y=x2 - четная функция.
На промежутке [0;+Ґ) функция возрастает.
На промежутке (-Ґ;0] функция убывает.
y=x2
Графиком является парабола.

Кубическая функция.
Функция y=x3
Свойства функции y=x3:
Область определения- вся числовая прямая
y=x3 -нечетная функция.
Функция возрастает на всей числовой прямой.
Графиком является кубическая
парабола.
y=x3

Квадратный корень.
Квадратным корнем называют также функцию x вещественной переменной x, которая каждому x0 ставит в соответствие арифметическое значение корня. Эта функция является частным случаем степенной функции x с a=21. Эта функция является гладкой при x > 0 , в нуле же она непрерывна справа, но не дифференцируема.
Свойства функции y=x
Область определения - луч [о;+∞) . Это следует из, того что выражение x определено лишь при x0.
Функция y=x ни четна, ни нечетна.
Функция y=x возрастает на луче [о;+ ∞)
Графиком является ветвь параболы в первой четверти.
У=√x

Модуль.
Функция модуль является биссектрисами первого и второго координатных углов.
Свойства:
Функция модуль является четной функцией .
Производная функции модуль в точке x=0 не существует .
График функции модуль симметричен относительно оси ординат .
у = | х |
{
|х | =
x, если х ≥ 0
-x, если х < 0

Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Табличный способ.
Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ.
Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ.
Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ.
Этот способ состоит в том, что функциональная зависимость выражается словами.
Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.
Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x - [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q ( r = [x]), где r — целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q
Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.

Свойства функции.
Область определения
Область значения
Монотонность
Ограниченность
Наибольшее, наименьшее значение
Непрерывность
Область значения
Выпуклость

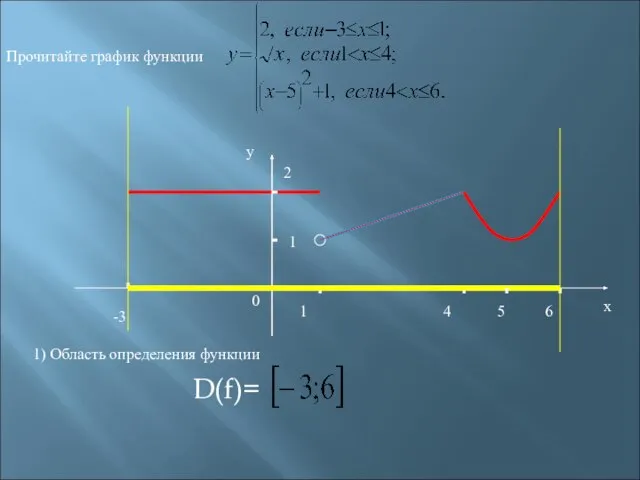
-3
1
2
1
4
6
х
у
0
Прочитайте график функции
5
1) Область определения функции
D(f)=

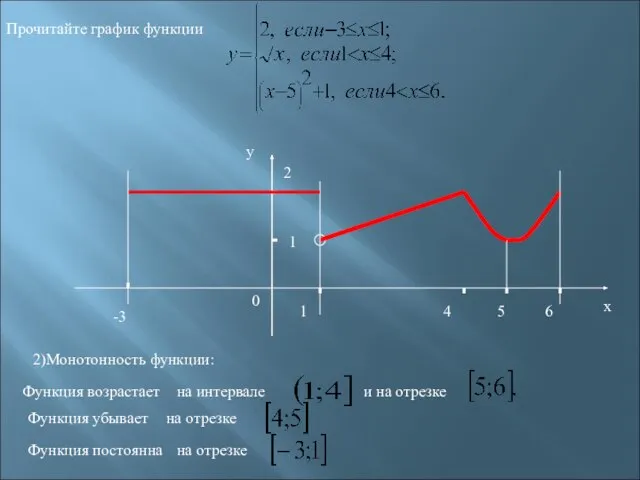
-3
1
2
1
4
6
х
у
0
Прочитайте график функции
2)Монотонность функции:
и на отрезке
5
Функция возрастает
на интервале
Функция убывает
на отрезке
Функция постоянна
на отрезке

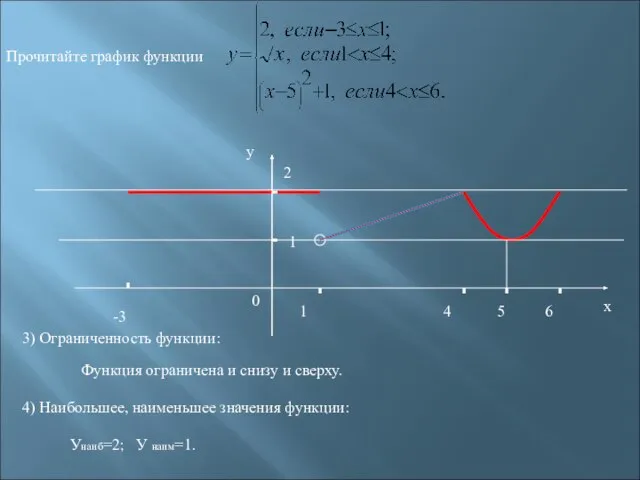
-3
1
2
1
4
6
х
у
0
Прочитайте график функции
5
3) Ограниченность функции:
Функция ограничена и снизу и сверху.
4) Наибольшее, наименьшее значения функции:
Унаиб=2; У наим=1.

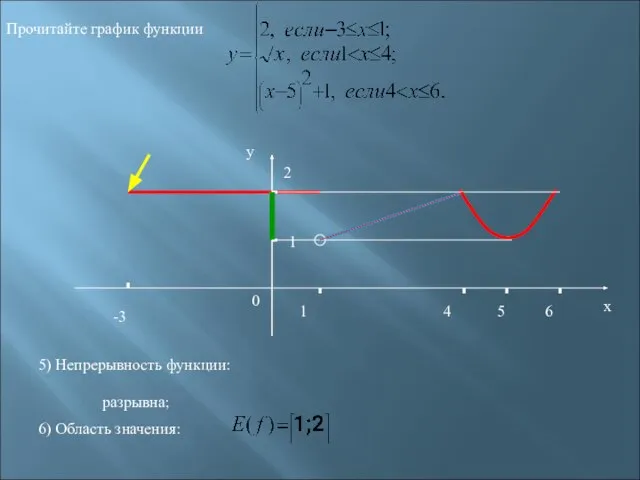
-3
1
2
1
4
6
х
у
0
Прочитайте график функции
6) Область значения:
5
5) Непрерывность функции:
разрывна;

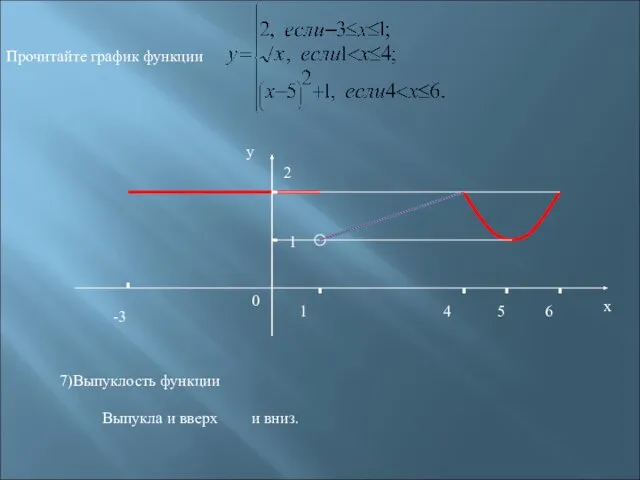
-3
1
2
1
4
6
х
у
0
Прочитайте график функции
5
7)Выпуклость функции
Выпукла и вверх
и вниз.

Свойства функции
6)
5)
разрывна;
1) D(f)=
и на отрезке
2) Функция возрастает
на интервале
Функция убывает
на отрезке
Функция постоянна
на отрезке
3)
4)
Унаиб=2; У наим=1.
Функция ограничена и снизу и сверху.
7) Выпукла и вверх и вниз.