История цифр и их связь с кодированием информации

Содержание
История цифр
Римские цифры
Цифры Майя
Цифра Ноль
Индийские цифры
Системы счисления
Позиционная система счисления
Не позиционная система
Шестнадцатеричная система
Перевод из одной системы в другую
Использование чисел
Транслятор систем счисления
Сложение чисел неограниченной длины
Выводы

История цифр.
Цифры — система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т. н. «арабские цифры»). Сочетания этих цифр порождают дву-(и более) значные числа.
Существуют также много других вариантов («алфавитов»):
Римские цифры(I V X L C D M)
Шестнадцатеричные цифры(0 1 2 3 4 5 6 7 8 9 A B C D E F)
Цифры майя (от 0 до 19)
в некоторых языках, например, в древнегреческом, в иврите, в церковнославянском, существует система записи чисел буквами.

Римские цифры
Цифры, использовавшиеся древними римлянами в своей не позиционной системе счисления.
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились около 500 лет до нашей эры у этрусков.

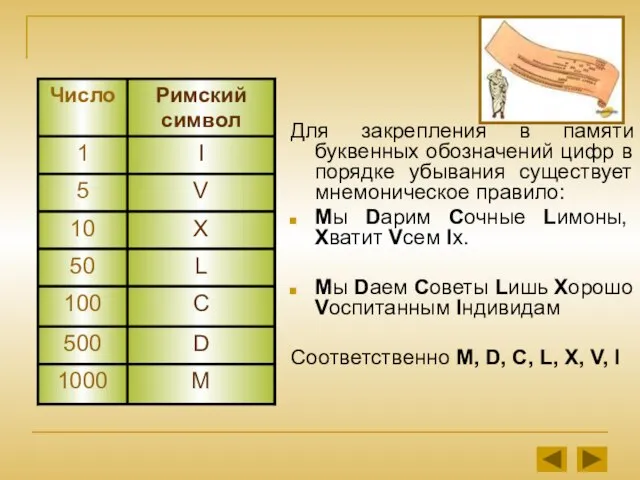
Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх.
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидам
Соответственно M, D, C, L, X, V, I

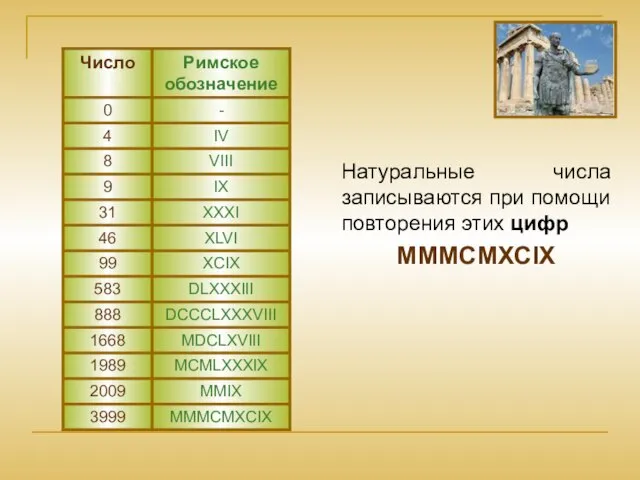
Натуральные числа записываются при помощи повторения этих цифр
MMMCMXCIX

Цифры Майя.
Позиционная запись, основанная в двадцатеричной системе счисления (по основанию 20), использовавшаяся цивилизацией Майя в доколумбовой Месоамерике.
Цифры майя составлялись из трёх элементов: нуля (знак ракушки), единицы (точка) и пятёрки(горизонтальная черта). Например, 19 писалось как четыре точки в горизонтальном ряду над тремя горизонтальными линиями

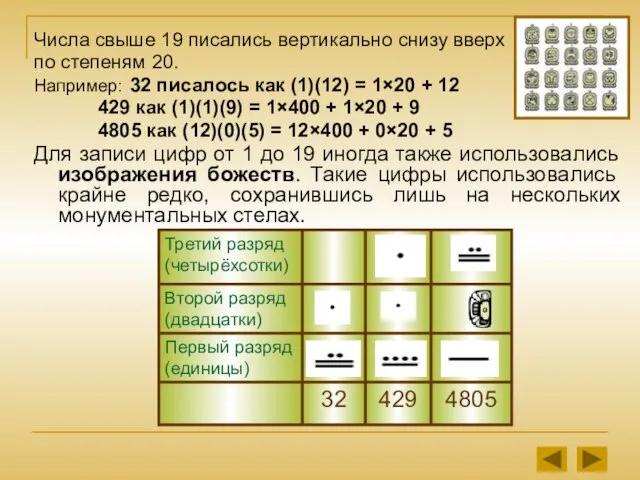
Числа свыше 19 писались вертикально снизу вверх
по степеням 20.
Например: 32 писалось как (1)(12) = 1×20 + 12
429 как (1)(1)(9) = 1×400 + 1×20 + 9
4805 как (12)(0)(5) = 12×400 + 0×20 + 5
Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах.

Цифра Ноль
Календарь Майя требовал использования нуля для обозначения пустого разряда. Первая дошедшая до нас дата с нулём (на стеле 2 в Чиапа-де Корсо, Чиапас) датирована 36 годом до н. э.
В календаре подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э.
В «долгом счёте» календаря майя была использована разновидность 20-ричной системы счисления, в которой второй разряд мог содержать только цифры от 0 до 17, после чего к третьему разряду добавлялась единица. Таким образом, единица третьего разряда означала не 400, а 18×20 = 360, что близко к числу дней в солнечном году.

Индийские цифры
Из истории известно, что в науке индийское происхождение так называемых арабских цифр было признано лишь в XIX веке.
Первым учёным, высказавшим эту, для того времени новую, мысль, был русский востоковед Георг Яковлевич Кер (1692—1740). Кер с 1731 года служил в Москве переводчиком коллегии иностранных дел.
Нет фото

Системы счисления
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
даёт представления множества чисел (целых или вещественных)
даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
отражает алгебраическую и арифметическую структуру чисел.
Системы счисления подразделяются на позиционные, непозиционные и смешанные

Позиционные системы счисления
В позиционных системах счисления один и тот же числовой знак(цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам ; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
К таким системам относится римская система записи чисел.

Шестнадцатеричная система счисления
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Широко используется в низкоуровневом программировании, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, до этого времени использовали восьмеричную систему.

Перевод чисел из одной системы счисления в другую
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например: число 5A316
5A316 = 3·160+10·161+5·16²= 3·1+10·16+5·256 = 144310
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
0101101000112 = 0101 1010 0011 = 5A316

Использование чисел
На монетах индийские цифры впервые появляются в 976 году в Испании, где имелись непосредственные связи с арабами.
Наиболее ранняя русская монета с индийскими цифрами относится к 1654 году. Славянские цифры в последний раз появляются на медных монетах чеканки 1718 года.

В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
В АДА и VHDL такие числа указывают так: «16#5A3#».
В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x».
В некоторых Ассемблерах используют букву «h», которую ставят после числа. При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов впереди ставится «0» (ноль): «0FFh» (25510)
Паскаль и некоторые версии Бейсика используют префикс «$».
Некоторые иные платформы, использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «&h».
В Unix-подобных операционных системах непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа

Транслятор систем счисления
Рассмотрим перевод чисел из десятичной системы в шестнадцатеричную и обратно. Для демонстрации перевода чисел была написана программа на языке Visual Basic.
Для перевода из одной системы счисления в другую необходимо ввести число в соответствующее поле и нажать на расположенную рядом командную кнопку. Результат перевода будет выведен в другое поле.

Сложение чисел
неограниченной длины
В процессорах компьютеров возможно проведение арифметических операциях для чисел ограниченной длины. При необходимости арифметические операции с числами произвольной длины могут быть осуществлены с помощью специальной программы. Для демонстрации решения была написана программа на языке Visual Basic суммирования чисел неограниченной длины.
Введите требуемые числа и нажмите кнопку «+». Результат будет в третьем поле.

Выводы
Особыми видами письменных знаков могут быть названы цифры
Цифры представляют собой исторические логограммы, служащие для краткого обозначения чисел
Для записи информации о количестве объектов используются числа, состоящие из цифр
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления.
Двоичная система используется для кодирования информации в компьютере
Шестнадцатеричная система – это компактная запись двоичных чисел
Цифровая система кодирования используется в языках программирования