Презентация по алгебре.

МАГИЧЕСКИЙ КВАДРАТ.
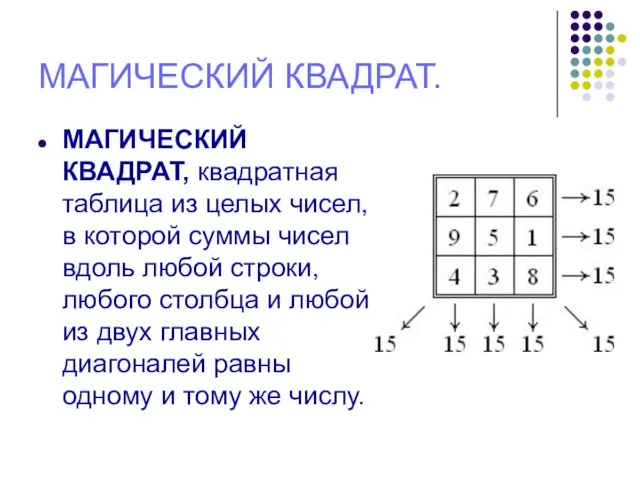
МАГИЧЕСКИЙ КВАДРАТ, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.

Легенда появления магического квадрата.
Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос.

Магический квадрат Ян Хуэя.
В 13 в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)

Квадрат А.Дюрера.
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера«Меланхолия I», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания картины (1514). Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и 3+5+12+14), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12).

Формула магического квадрата.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел. Сумма M чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна .Доказано, что n ≥ 3. Для квадрата 3-го порядка S = 15, 4-го порядка – S = 34, 5-го порядка – S = 65.

МЕТОД ДЕ ЛА ИРА.
Метод Де Ла Ира (1640–1718) основан на двух первоначальных квадратах. На рисунке показано, как с помощью этого метода строится квадрат 5-го порядка. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз (рис. б). Поклеточная сумма этих двух квадратов (рис. в) образует магический квадрат. Этот метод используется и при построении квадратов четного порядка.

Построение магических квадратов
Метод террас
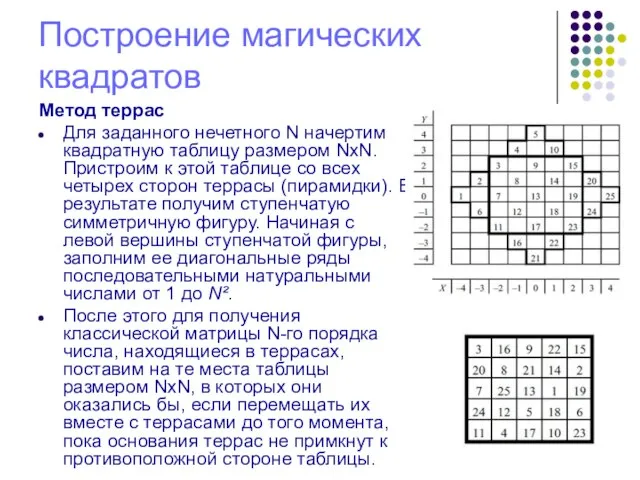
Для заданного нечетного N начертим квадратную таблицу размером NxN. Пристроим к этой таблице со всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру. Начиная с левой вершины ступенчатой фигуры, заполним ее диагональные ряды последовательными натуральными числами от 1 до N².
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.