Содержание
- 2. Функция — одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль
- 3. Пропедевтический период (с древнейших времен до 17 века) Идея функциональной зависимости восходит к древности. Ее содержание
- 4. Введение понятия функции через механическое и геометрическое представления (17 век) Начиная лишь с 17 века в
- 5. Кроме того, у Декарта и Ферма (1601 – 1665) в геометрических работах появляется отчетливое представление переменной
- 6. Аналитическое определение функции (17 – начало 19 века) Само слово "функция" (от латинского functio — совершение,
- 7. Наряду с этим Эйлер предлагает использовать буквы F, Y и другие. Даламбер сделал шаг вперед на
- 8. Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в
- 9. Из трудов Фурье следовало, что любая кривая, независимо от того, из скольких и каких разнородных частей
- 10. Идея соответствия (19 век) В 1834 году в работе "Об исчезании тригонометрических строк" Н. И. Лобачевский,
- 11. Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано. Таким
- 12. Эта функция задана двумя формулами и словесно. Она играет известную роль в анализе. Аналитически ее можно
- 14. Скачать презентацию
Слайд 2Функция — одно из основных математических и общенаучных понятий. Оно сыграло и
Функция — одно из основных математических и общенаучных понятий. Оно сыграло и
Слайд 3Пропедевтический период
(с древнейших времен до 17 века)
Идея функциональной зависимости восходит к
Пропедевтический период
(с древнейших времен до 17 века)
Идея функциональной зависимости восходит к

Слайд 4Введение понятия функции через механическое и геометрическое представления (17 век)
Начиная лишь с
Введение понятия функции через механическое и геометрическое представления (17 век)
Начиная лишь с

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных — последними буквами латинского алфавита: x, y, z, известных — начальными буквами того же алфавита: a, b, c,... и т. д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
Слайд 5Кроме того, у Декарта и Ферма (1601 – 1665) в геометрических работах
Кроме того, у Декарта и Ферма (1601 – 1665) в геометрических работах

В "Геометрии" Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило, по существу, интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых — функция от абсцисс (x); путь и скорость — функция от времени (t) и т. п.
Слайд 6Аналитическое определение функции (17 – начало 19 века)
Само слово "функция" (от латинского
Аналитическое определение функции (17 – начало 19 века)
Само слово "функция" (от латинского

Слайд 7Наряду с этим Эйлер предлагает использовать буквы F, Y и другие. Даламбер
Наряду с этим Эйлер предлагает использовать буквы F, Y и другие. Даламбер

Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во "Введении в анализ бесконечного"): "Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств". Так понимали функцию на протяжении почти всего 18 века Даламбер (1717 – 1783), Лагранж (1736 – 1813), Фурье (1768 – 1830) и другие видные математики. Что касается Эйлера, то он не всегда придерживался вышеуказанного определения; в его работах понятие функции подвергалось дальнейшему развитию в соответствии с запросами математического анализа.
В "Дифференциальном исчислении", вышедшем в свет в 1755 году, Эйлер дает общее определение функции: "Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых". "Это наименование, — продолжает далее Эйлер, — имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество определяется с помощью других".
Слайд 8Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим
Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим
Одним из нерешенных вопросов, связанных с понятием функции, по поводу которого велась ожесточенная борьба мнений, был следующий: можно ли одну функцию задать несколькими аналитическими выражениями?
Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768 – 1830), занимавшийся в основном математической физикой. В представляемых им в Парижскую АН в 1807 – 1811 гг. "Мемуарах по теории распространения тепла в твердом теле", Фурье привел и первые примеры функций, которые заданы на различных участках различными аналитическими выражениями.
Слайд 9Из трудов Фурье следовало, что любая кривая, независимо от того, из скольких
Из трудов Фурье следовало, что любая кривая, независимо от того, из скольких

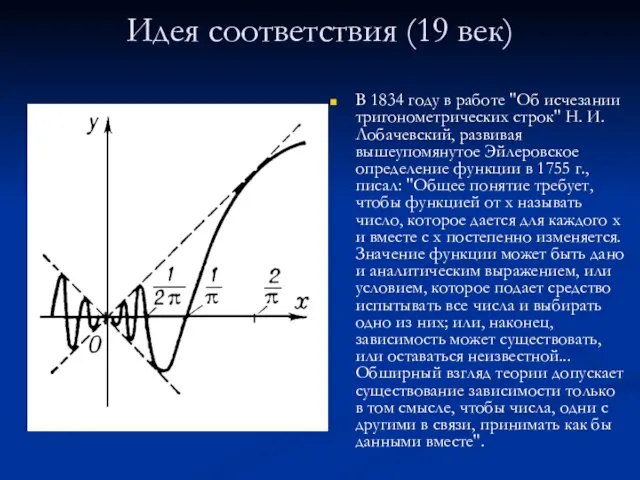
Слайд 10Идея соответствия (19 век)
В 1834 году в работе "Об исчезании тригонометрических строк"
Идея соответствия (19 век)
В 1834 году в работе "Об исчезании тригонометрических строк"
Слайд 11Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским
Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским

Примером, соответствующим этому общему определению, может служить так называемая "функция Дирихле" j(x).
Слайд 12Эта функция задана двумя формулами и словесно. Она играет известную роль в
Эта функция задана двумя формулами и словесно. Она играет известную роль в

Во второй половине 19 века после создания теории множеств в понятие функции, помимо идеи соответствия была включена и идея множества. Таким образом, в полном своем объеме общее определение понятия функции формулируется следующим образом: если каждому элементу x множества А поставлен в соответствие некоторый определенный элемент y из множества В, то говорят, что на множестве А задана функция y = f(x), или что множество А отображено на множество В. В первом случае элементы x множества А называют значениями аргумента, а элементы их множества В — значениями функции; во втором случае x — прообразы, y — образы. В современном смысле рассматривают функции, определенные для множества значений x, которые, возможно, и не заполняют отрезка a < x < b, о котором говорится в определении Дирихле. Достаточно указать, например, на функцию-факториал y = n, заданную на множестве натуральных чисел. Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам. Например, к геометрическим фигурам. При любом геометрическом преобразовании мы имеем дело с функцией. Другими синонимами термина "функция" в различных отделах математики являются: соответствие, отображение, оператор, функционал и др.
Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим
 Африка
Африка Тууль Максим Юрьевич «Клуб Участников Проектного Процесса», Директор АКБ «Надежный банк», Президент тел: (495) 7675=02=23; E-mail: TMY@proje
Тууль Максим Юрьевич «Клуб Участников Проектного Процесса», Директор АКБ «Надежный банк», Президент тел: (495) 7675=02=23; E-mail: TMY@proje Илларион Михайлович Прянишников (1840-1894)
Илларион Михайлович Прянишников (1840-1894) ТЕРРИТОРИЯ ЛЮБВИ
ТЕРРИТОРИЯ ЛЮБВИ Презентация на тему И.С. Тургенева «Муму»
Презентация на тему И.С. Тургенева «Муму»  Презентація 10 клас Урок 31
Презентація 10 клас Урок 31 Ассирийская держава
Ассирийская держава Презентация 2
Презентация 2 Сертификация систем качества
Сертификация систем качества История развития зоологии
История развития зоологии Реализуемое имущество АО РоссельхозБанк: транспортные средства, с/х техника и оборудование
Реализуемое имущество АО РоссельхозБанк: транспортные средства, с/х техника и оборудование Обработка нижних срезов рукавов
Обработка нижних срезов рукавов Давайте знакомиться!
Давайте знакомиться! Мой первый бизнес-план
Мой первый бизнес-план Украшения своими руками
Украшения своими руками Стратегическое планирование и его этапы. Планирование маркетинга. Контроль. Типы маркетингового контроля
Стратегическое планирование и его этапы. Планирование маркетинга. Контроль. Типы маркетингового контроля Требования к информации, формируемой в бухгалтерском учете
Требования к информации, формируемой в бухгалтерском учете Центр«Интеллектуальные электронные энергосберегающие системы»(ЦИЭС)
Центр«Интеллектуальные электронные энергосберегающие системы»(ЦИЭС) Защитные очки
Защитные очки Карельский научный центр Российской академии наук. Молодые учёные
Карельский научный центр Российской академии наук. Молодые учёные История Т-34
История Т-34 По страницам русского языка
По страницам русского языка Ксюша
Ксюша Урок 20.1. Перевод дела в архив (на примере гражданского дела)
Урок 20.1. Перевод дела в архив (на примере гражданского дела) Презентация на тему Имена существительные нарицательные и собственные
Презентация на тему Имена существительные нарицательные и собственные Аудитория украинского интернета: статистика и тенденции
Аудитория украинского интернета: статистика и тенденции Любить но кого же?
Любить но кого же? Право, семья, ребенокКравченко, 9 класс
Право, семья, ребенокКравченко, 9 класс