Содержание
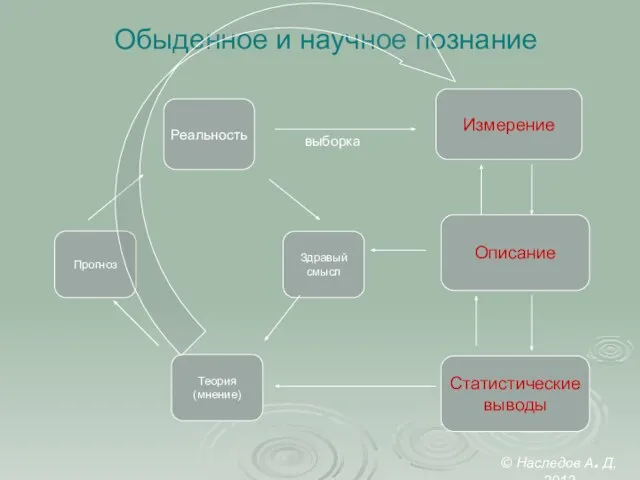
- 2. Обыденное и научное познание Измерение Описание Статистические выводы Реальность выборка © Наследов А. Д, 2012
- 3. ГС и выборка Репрезентативность Случайный отбор и доступность Детальное описание выборки и процедуры ее формирования Сравнение
- 4. Первый опыт проверки статистической достоверности Арбутнот: «Свидетельство в пользу божественного провидения, полученное путем систематического наблюдения за
- 5. Гипотезы: содержательные и статистические 1. Содержательная гипотеза: утверждение о связи 2-х явлений в ГС. 2. В
- 6. Теоретическое распределение и p-уровень значимости Пример: проверка состоятельности тестовой нормы IQ = 100. Выборочные статистики: Статистическая
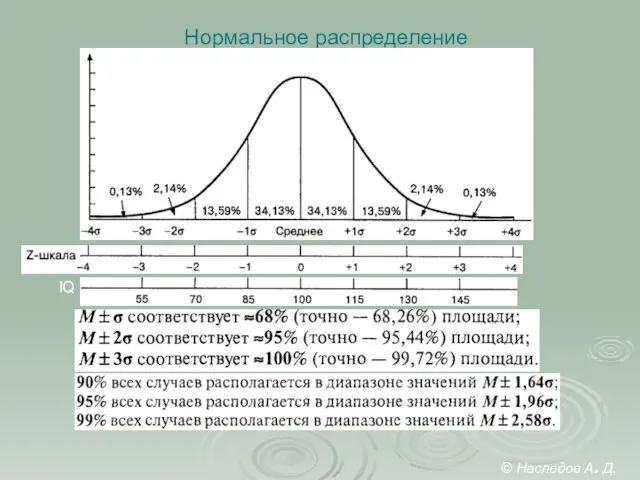
- 7. Нормальное распределение IQ © Наследов А. Д, 2012
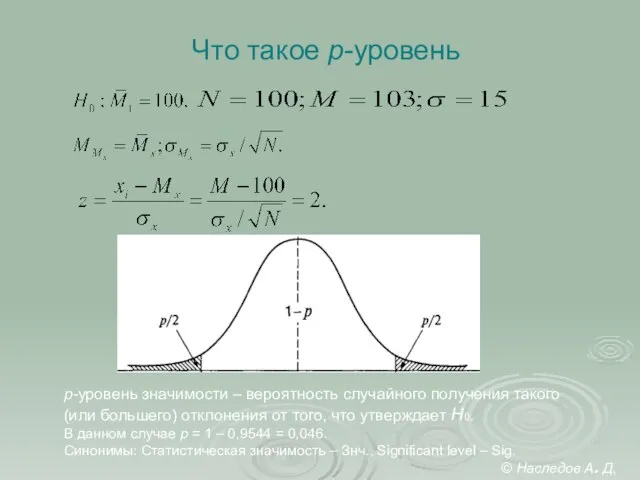
- 8. Что такое p-уровень p-уровень значимости – вероятность случайного получения такого (или большего) отклонения от того, что
- 9. Статистический критерий - z-критерий. - t-критерий Стьюдента. © Наследов А. Д, 2012
- 10. Статистическое решение 1-α 1-β p: 0 1 α - H0 не отклоняется; - Н0 отклоняется. ©
- 11. © Наследов А. Д, 2012
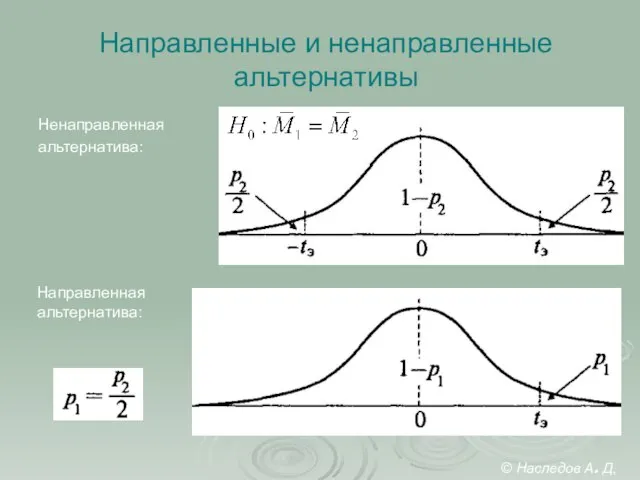
- 12. Направленные и ненаправленные альтернативы Ненаправленная альтернатива: Направленная альтернатива: © Наследов А. Д, 2012
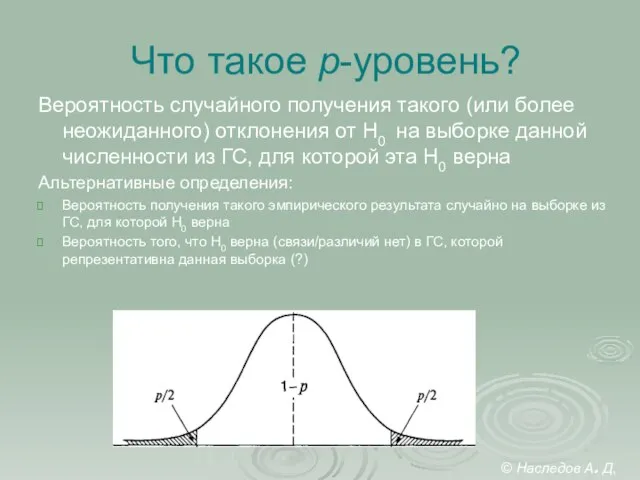
- 13. Что такое p-уровень? Вероятность случайного получения такого (или более неожиданного) отклонения от Н0 на выборке данной
- 14. Типичные ошибки интерпретации p-уровня значимости © Наследов А. Д, 2012
- 15. 1. Содержательная интерпретация Подтверждение содержательной гипотезы (а не ее доказательство) Отклонение H0 Принятие H0 НЕ подтверждение
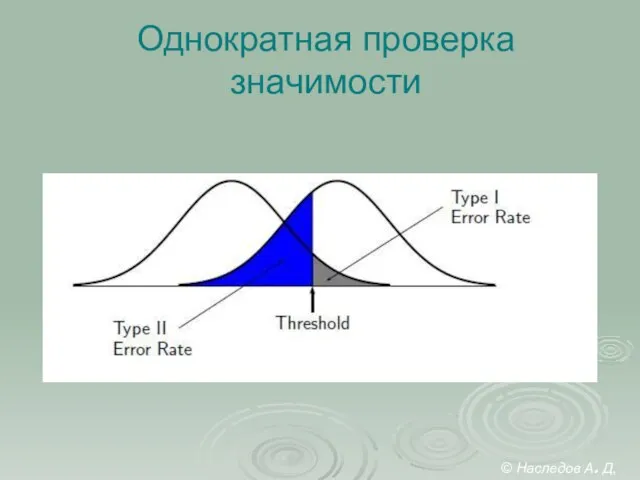
- 16. Однократная проверка значимости © Наследов А. Д, 2012
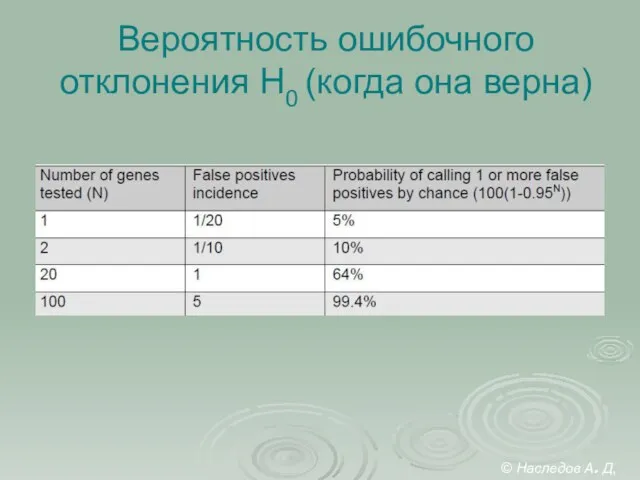
- 17. Вероятность ошибочного отклонения Н0 (когда она верна) © Наследов А. Д, 2012
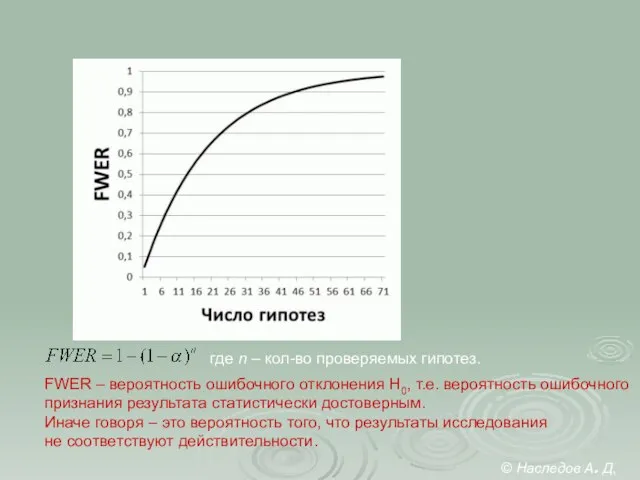
- 18. FWER – вероятность ошибочного отклонения H0, т.е. вероятность ошибочного признания результата статистически достоверным. Иначе говоря –
- 19. Учет множественности статистических проверок Применение многомерных методов Поправка Бонферрони для семейства n гипотез: для n гипотез
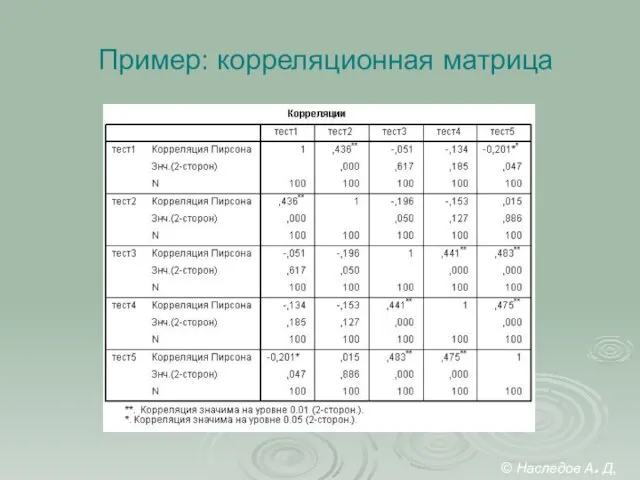
- 20. Пример: корреляционная матрица © Наследов А. Д, 2012
- 21. Последствия коррекции многократной проверки значимости При одном и том же пороге принятия/отклонения Н0 (α – серая
- 22. Рекомендации Минимизировать кол-во измерений за счет увеличения их надежности и валидности Применять многомерные методы для большого
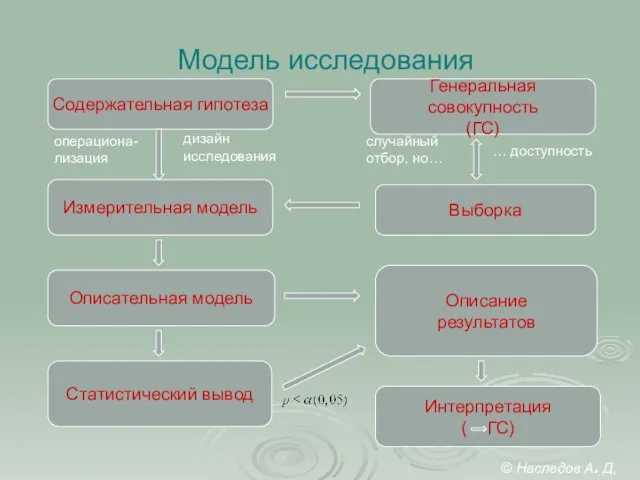
- 23. Модель исследования Содержательная гипотеза Измерительная модель Статистический вывод Генеральная совокупность (ГС) Выборка Интерпретация ( ГС) Описательная
- 24. Измерения и шкалы Объекты (случаи) Свойства и их признаки Переменные – результаты измерений Измерения в психологии
- 25. Измерительные шкалы Номинативная (номинальная, наименований, неколичественная). Операция – классификация. Пол, хобби, должность… Порядковая (ранговая) – количественная,
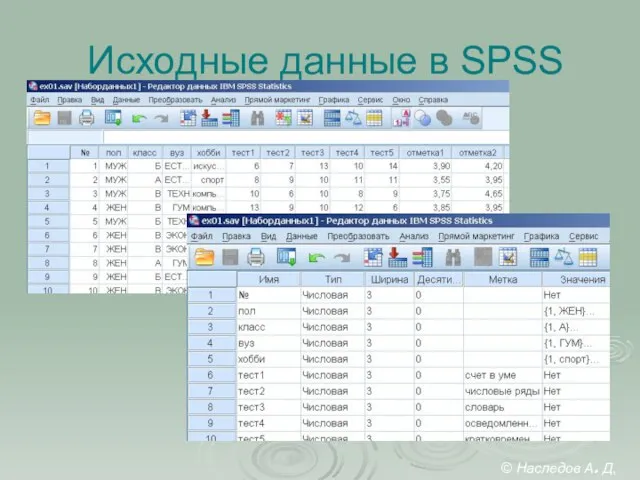
- 26. Исходные данные в SPSS © Наследов А. Д, 2012
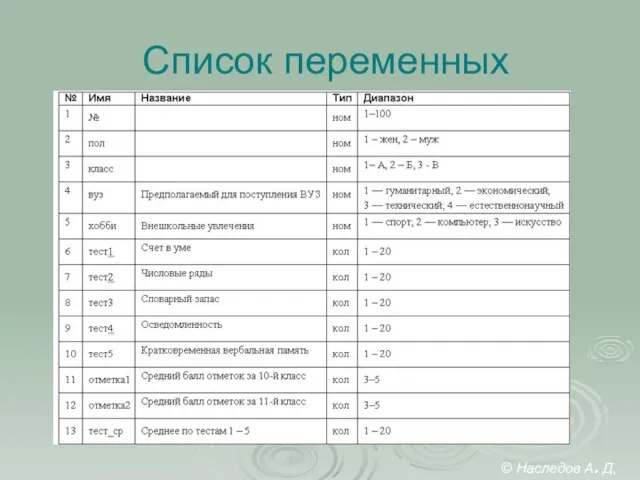
- 27. Список переменных © Наследов А. Д, 2012
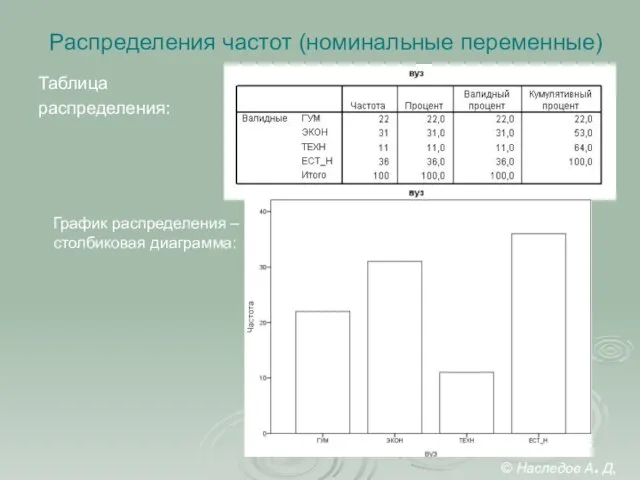
- 28. Распределения частот (номинальные переменные) Таблица распределения: График распределения – столбиковая диаграмма: © Наследов А. Д, 2012
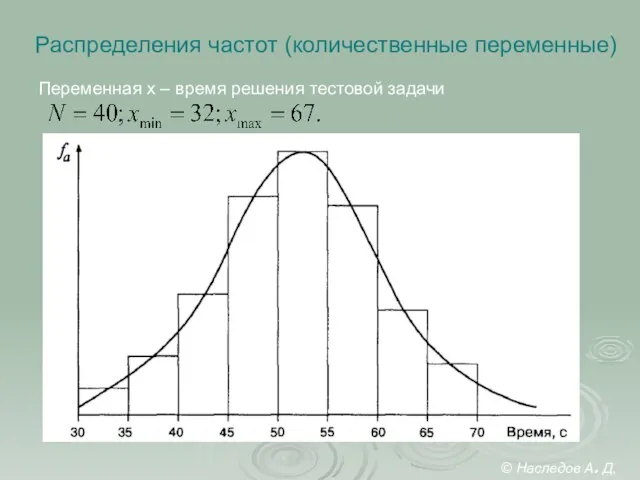
- 29. Распределения частот (количественные переменные) Переменная x – время решения тестовой задачи © Наследов А. Д, 2012
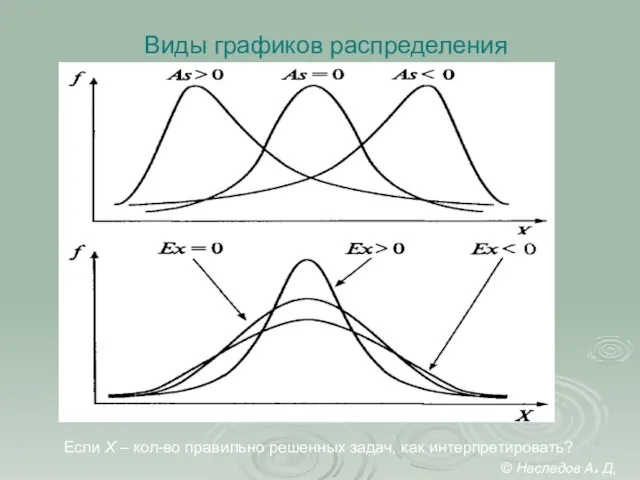
- 30. Виды графиков распределения Если Х – кол-во правильно решенных задач, как интерпретировать? © Наследов А. Д,
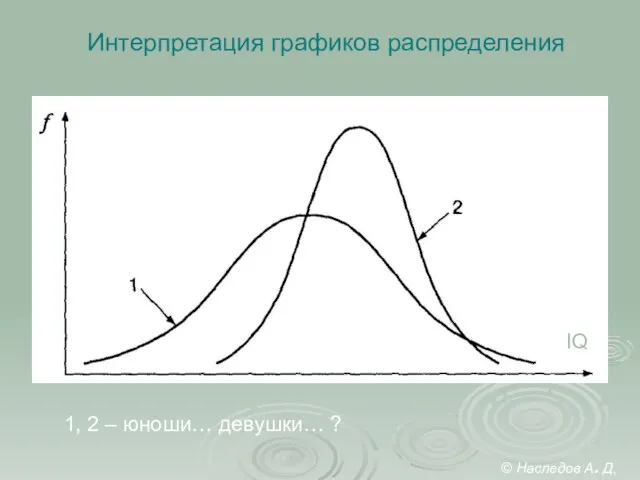
- 31. Интерпретация графиков распределения IQ 1, 2 – юноши… девушки… ? © Наследов А. Д, 2012
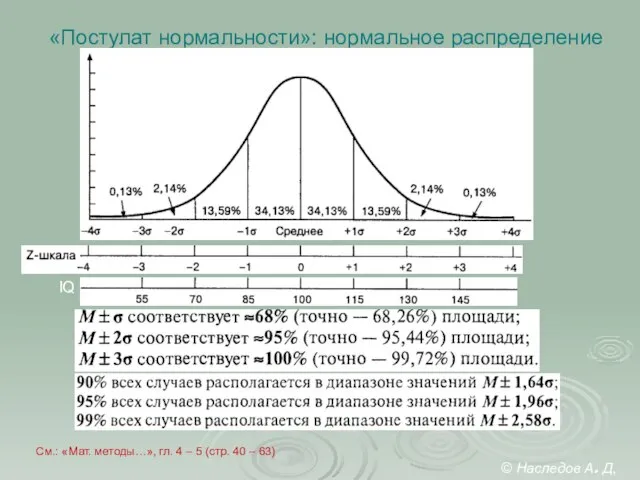
- 32. «Постулат нормальности»: нормальное распределение IQ © Наследов А. Д, 2012 См.: «Мат. методы…», гл. 4 –
- 33. Проверка нормальности Зачем? Визуально, по графику распределения и с контролем выбросов. По критериям асимметрии и эксцесса.
- 35. Скачать презентацию















 Многогранники в архитектуре и живописи
Многогранники в архитектуре и живописи Инженерно-геодезические изыскания под реконструкцию здания дворца культуры г. Стерлитамак, Республика Башкортостан
Инженерно-геодезические изыскания под реконструкцию здания дворца культуры г. Стерлитамак, Республика Башкортостан Вторая Мировая война
Вторая Мировая война Цитаты из Нового завета в патристических сочинениях
Цитаты из Нового завета в патристических сочинениях Интеграция инновационной России и мира –основа коммуникаций
Интеграция инновационной России и мира –основа коммуникаций А А Career in law FBI Agent
А А Career in law FBI Agent  Атлетическая гимнастика
Атлетическая гимнастика 4
4 Tema_9_Konstitutsionno-pravovoy_status_cheloveka_i_grazhdanina
Tema_9_Konstitutsionno-pravovoy_status_cheloveka_i_grazhdanina Молодёжные субкультуры
Молодёжные субкультуры Мой выбор
Мой выбор Деревья (антонимы)
Деревья (антонимы) Коррекция самооценки подростков средствами фототерапии
Коррекция самооценки подростков средствами фототерапии Трудовые правоотношения и заключение трудового договора
Трудовые правоотношения и заключение трудового договора Презентация на тему Звуковые колебания
Презентация на тему Звуковые колебания Предложения с обособленными членами
Предложения с обособленными членами Готов к труду и обороне
Готов к труду и обороне Презентация на тему Особенности морали
Презентация на тему Особенности морали  Как выбрать свой платок
Как выбрать свой платок Построение изометрической проекции окружности. Алгоритм построения
Построение изометрической проекции окружности. Алгоритм построения Осенью
Осенью Kazakhstan in 70 -1991 years
Kazakhstan in 70 -1991 years Componentele unui geam
Componentele unui geam История возникновения гимнастики
История возникновения гимнастики Школьная успеваемость
Школьная успеваемость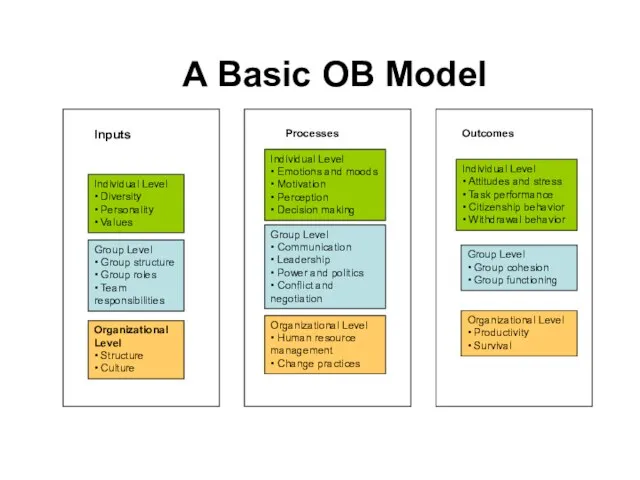 A Basic OB Model
A Basic OB Model великие просветители Европы
великие просветители Европы Древнейшие цивилизации
Древнейшие цивилизации