Содержание
- 2. * Это нужно знать Здравствуйте. Перед экзаменом Вам по графику назначены консультации, и предлагаемая ниже, информация
- 3. * Это нужно знать
- 4. К экзамену нужно знать:
- 5. Задача. Построить проекции точек по координатам, заданным в миллиметрах (x,y,z): А(30,15,30); В(10,25,0) С(10,25,20). Совпадение проекций в
- 6. Рис. 1. Комплексный чертёж и наглядное изображение точки А x z y o A2 A1 Π2
- 7. Для создания комплексного чертежа (см. рис.) для точки, необходимо по её координатам А (45, 36,25 )
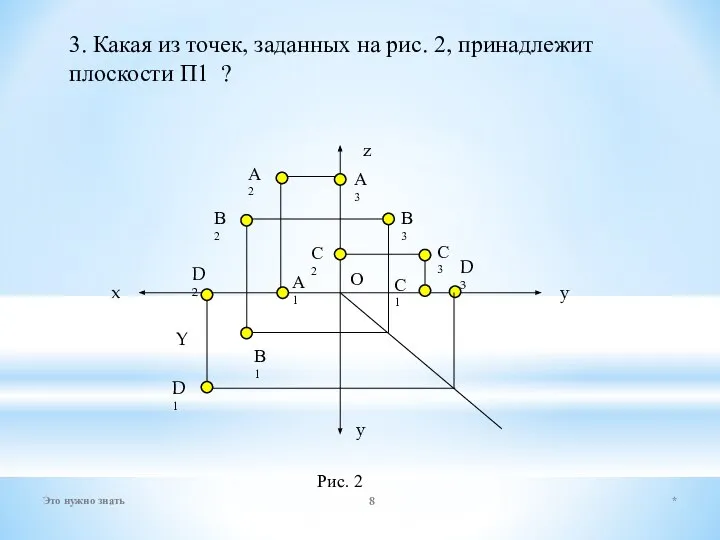
- 8. 3. Какая из точек, заданных на рис. 2, принадлежит плоскости П1 ? x y z y
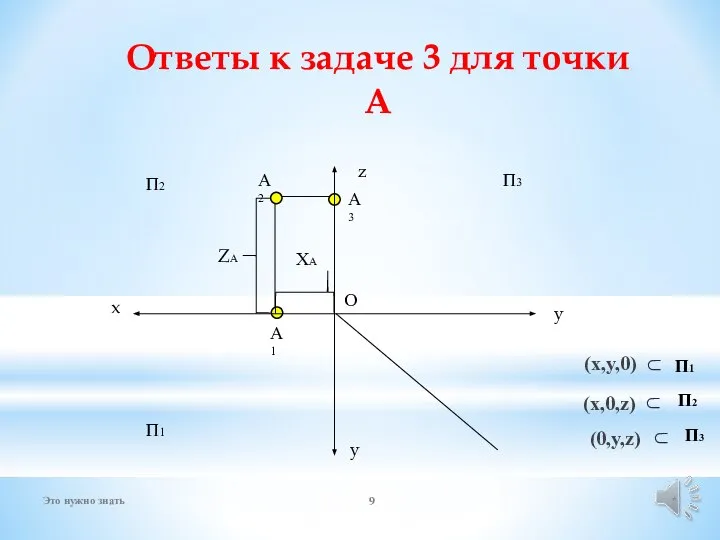
- 9. Ответы к задаче 3 для точки А x ХА ZА * Это нужно знать
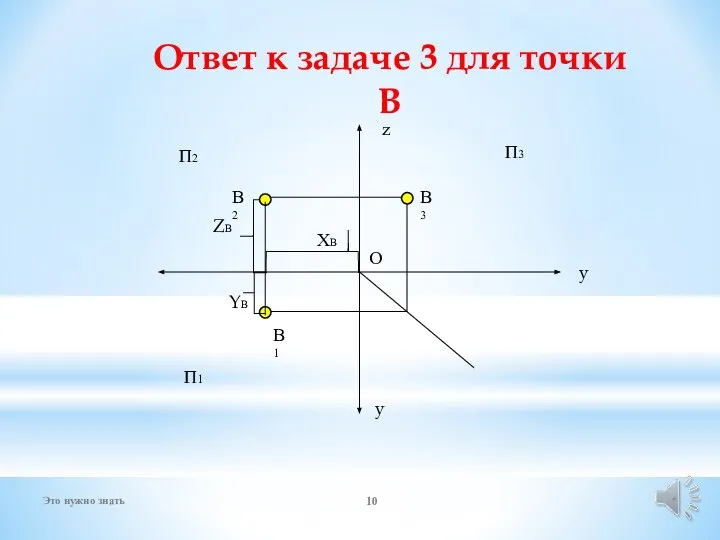
- 10. П1 П2 П3 Ответ к задаче 3 для точки В * Это нужно знать
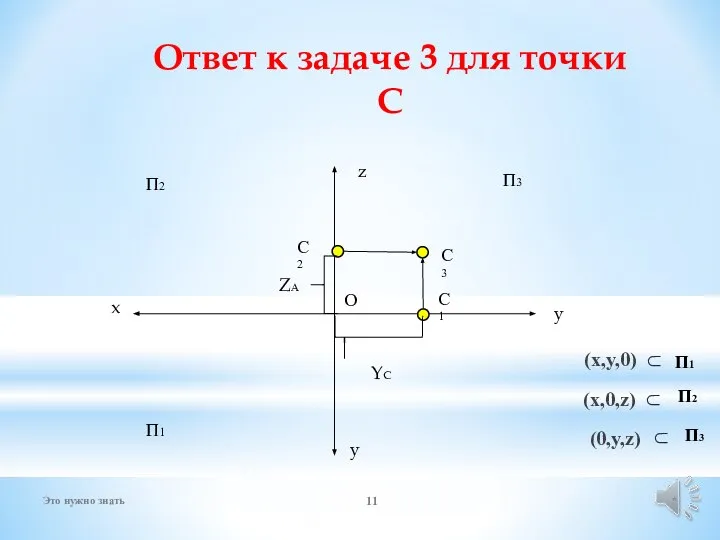
- 11. x С3 С2 С1 YC ZА Ответ к задаче 3 для точки С * Это нужно
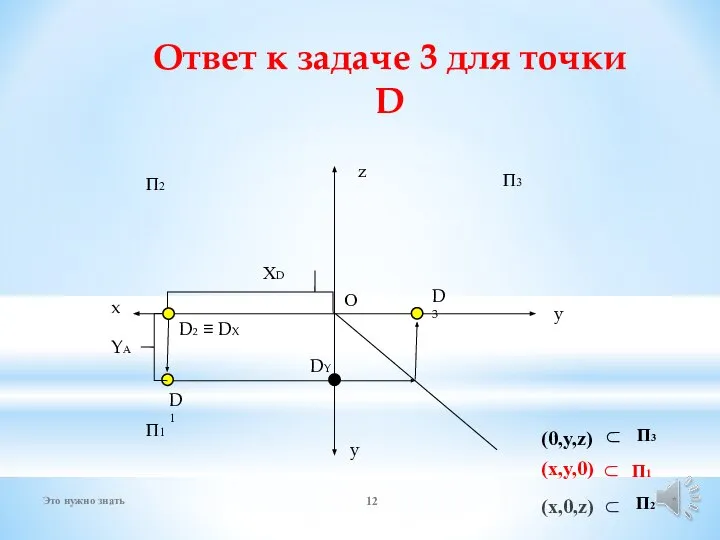
- 12. x D3 D1 ХD YА D2 ≡ DX DY Ответ к задаче 3 для точки D
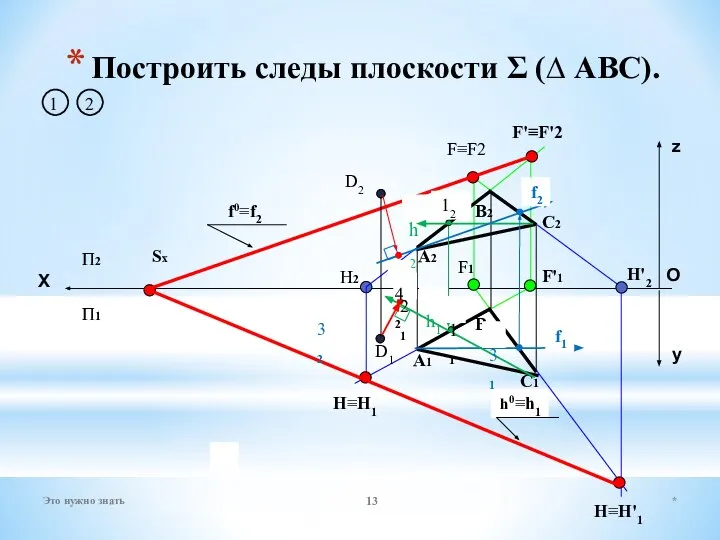
- 13. Построить следы плоскости Σ (∆ АВС). А1 А2 В2 В1 С2 С1 Sx F1 H2 F≡F2
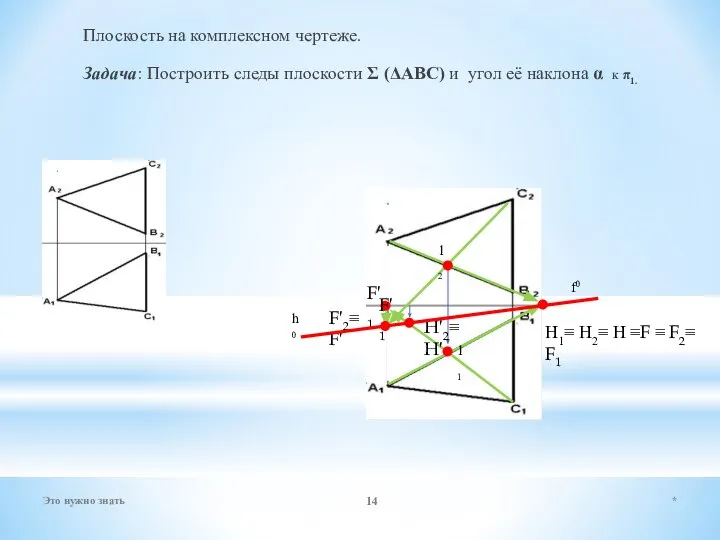
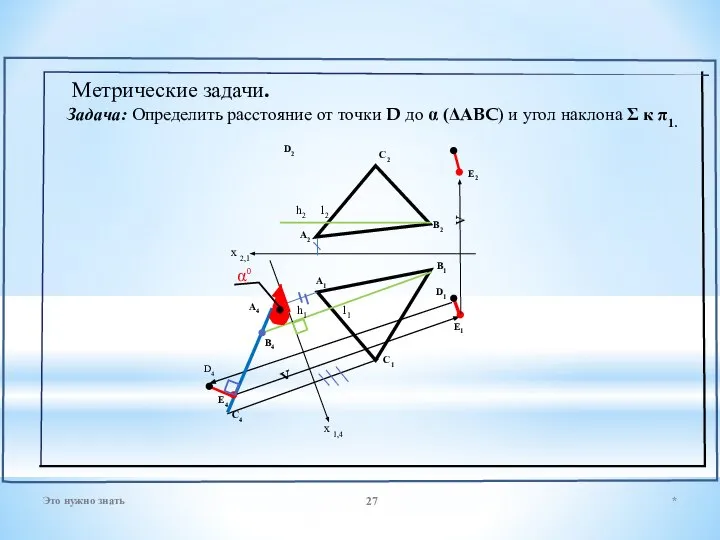
- 14. Плоскость на комплексном чертеже. Задача: Построить следы плоскости Σ (ΔАBC) и угол её наклона α к
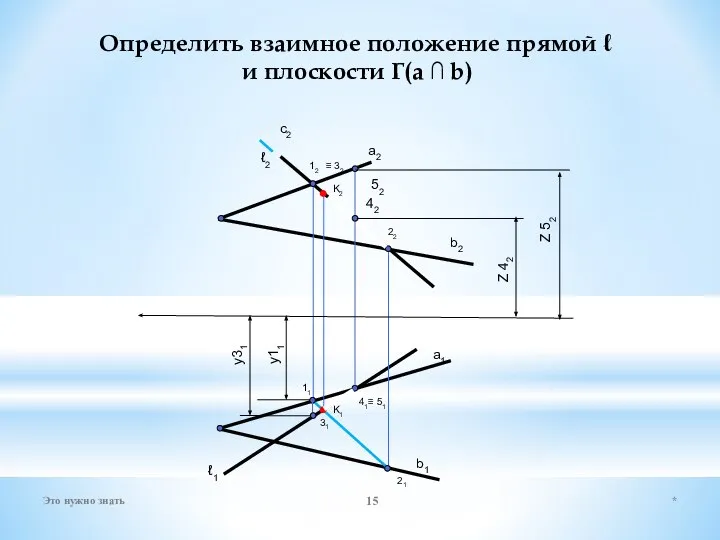
- 15. Определить взаимное положение прямой ℓ и плоскости Г(a ∩ b) a2 b2 ℓ1 a1 b1 12
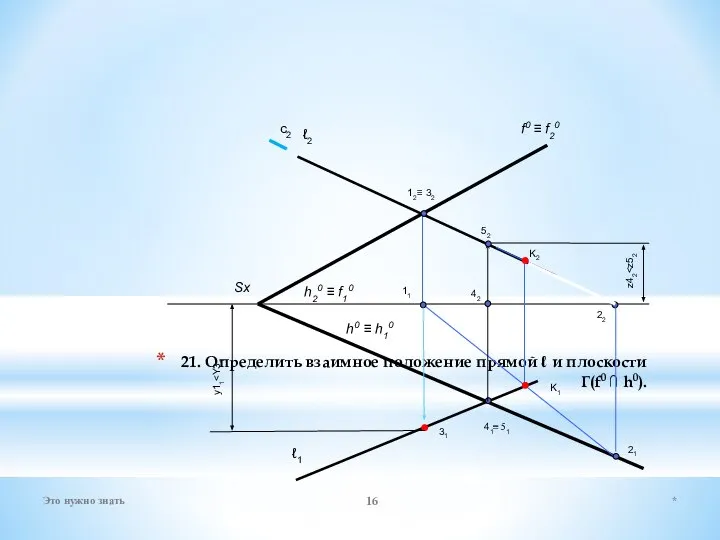
- 16. 21. Определить взаимное положение прямой ℓ и плоскости Г(f0 ∩ h0). ℓ2 ℓ1 Sx 12 K2
- 17. f0 ≡ f20 h0 ≡ h10 22 21 12 11 ℓ1 ℓ2 14 24 М2 31
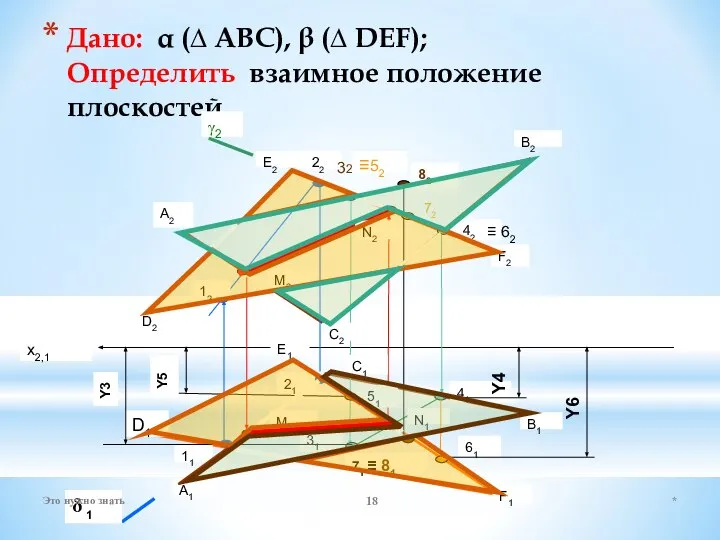
- 18. Дано: α (∆ ABC), β (∆ DEF); Определить взаимное положение плоскостей A2 A1 В2 В1 С1
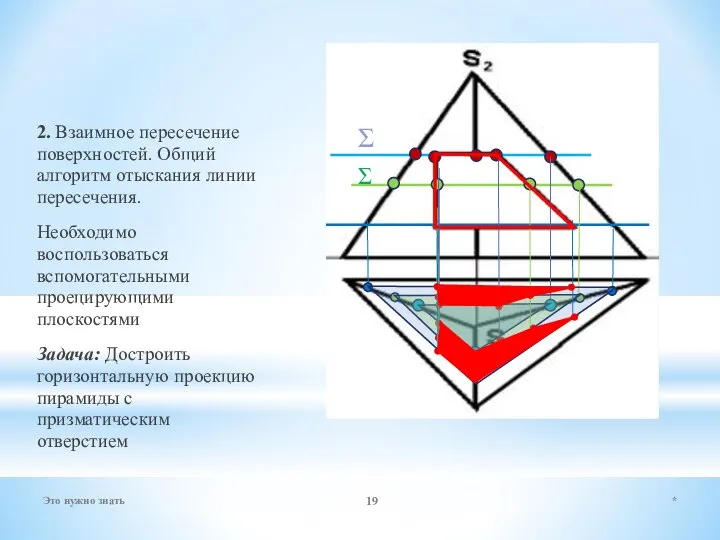
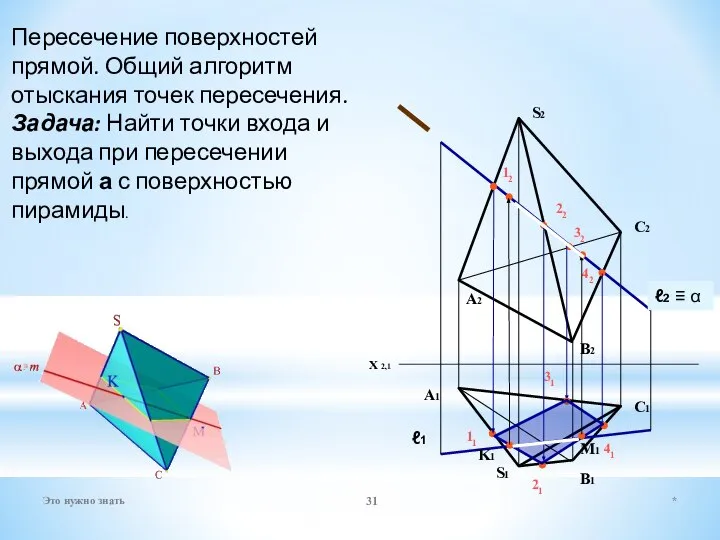
- 19. 2. Взаимное пересечение поверхностей. Общий алгоритм отыскания линии пересечения. Необходимо воспользоваться вспомогательными проецирующими плоскостями Задача: Достроить
- 20. Виды проецирования в начертательной геометрии. Сущность, практическое применение и свойства ортогонального проецирования. (С графическими пояснениями *
- 21. Виды проецирования В начертательной геометрии изображения получают графическим методом с использованием операции проецирования (от латинского projectio
- 22. Центральное проецирование Сущность центрального проецирования заключается в том, что при этом виде должен быть центр проецирования
- 23. Параллельное проецирование Является частным случаем центрального проецирования в котором центр проецирования S удален в бесконечность и
- 24. Свойства параллельного проецирования При параллельном проецировании сохраняются следующие свойства: 1. Проекция точки есть точка. 2. Проекция
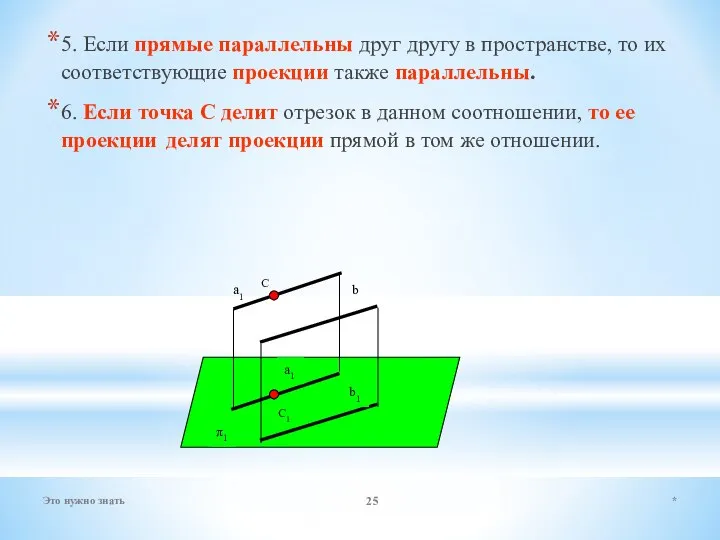
- 25. 5. Если прямые параллельны друг другу в пространстве, то их соответствующие проекции также параллельны. 6. Если
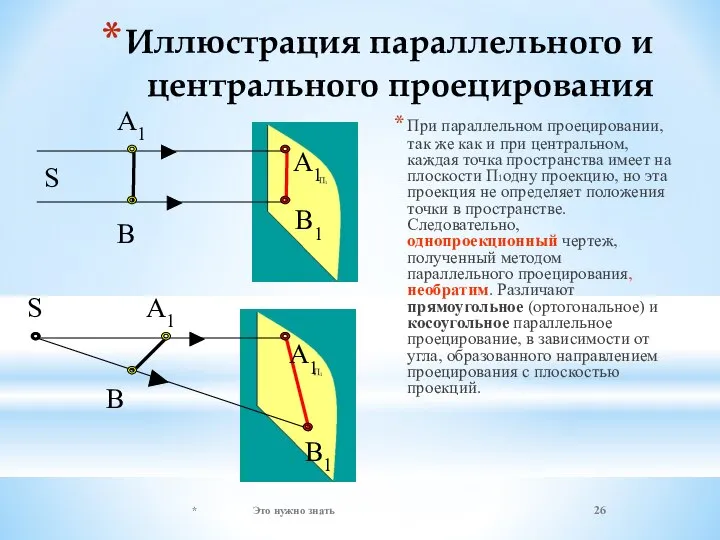
- 26. Иллюстрация параллельного и центрального проецирования При параллельном проецировании, так же как и при центральном, каждая точка
- 27. h2 С2 А2 В2 С1 А1 В1 х 1,4 х 2,1 h1 D2 D1 D4 С4
- 28. S2 S1 a2 П1 П2 12 11 14 S4 A4 C2 ≡D2 C1 B1 D1 A1
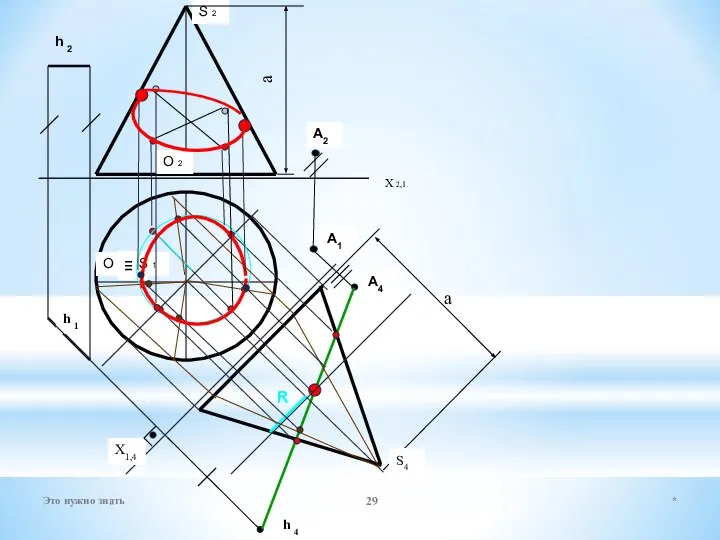
- 29. X 2,1 S 2 O 2 O 1 ≡ S 1 h 2 h 1 A1
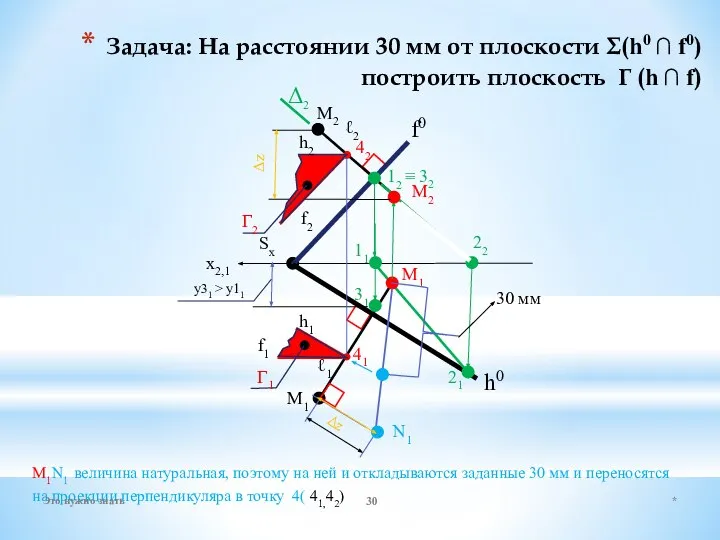
- 30. Задача: На расстоянии 30 мм от плоскости Σ(h0 ∩ f0) построить плоскость Γ (h ∩ f)
- 31. X 2,1 А2 А1 С1 С2 В1 В2 S2 S1 ℓ1 ℓ2 ℓ2 ≡ α 11
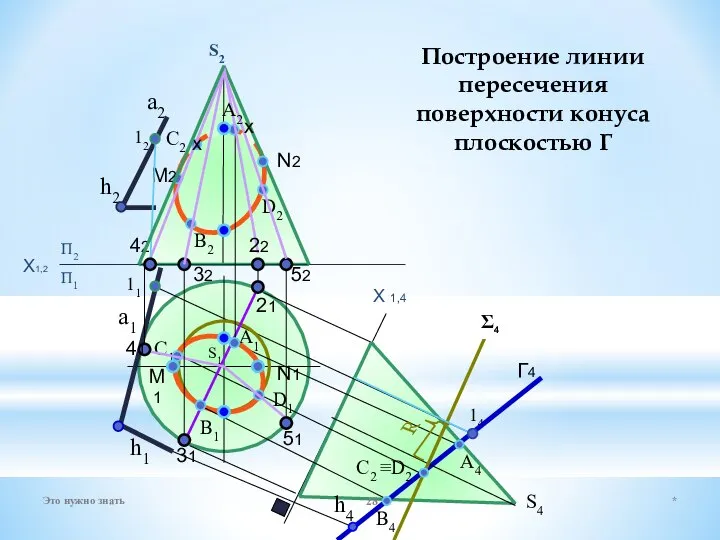
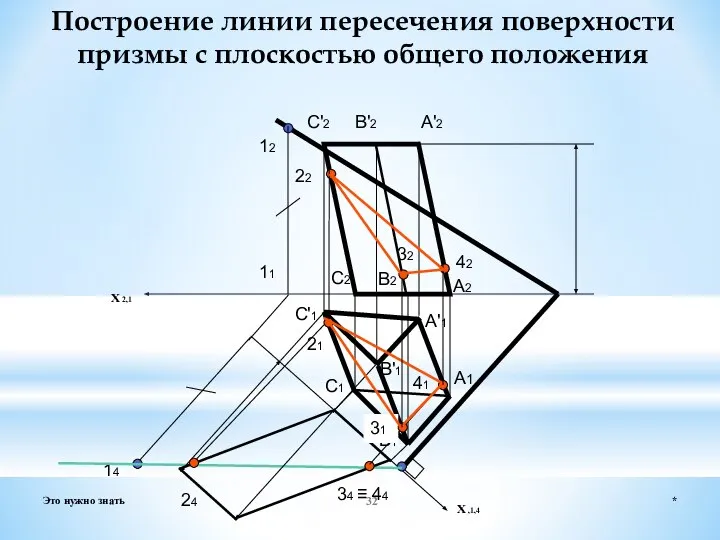
- 32. * Это нужно знать Построение линии пересечения поверхности призмы с плоскостью общего положения X 2,1 А1
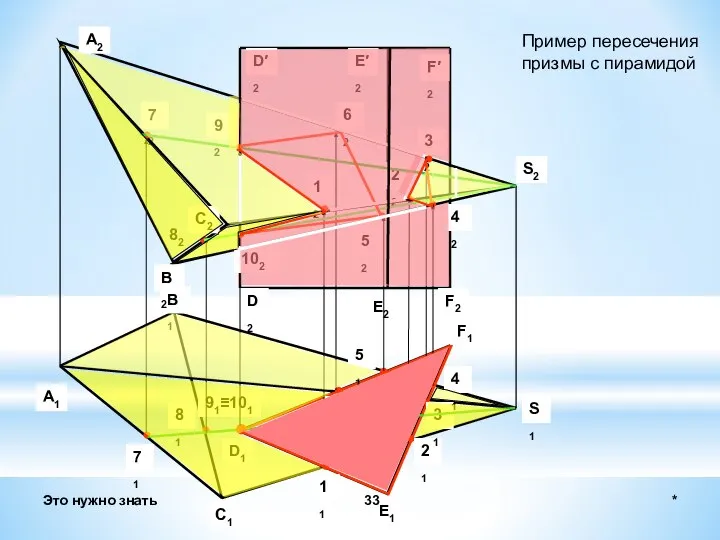
- 33. B1 C1 A1 B2 C2 A2 S2 S1 F2 E2 D2 F′2 E′2 D′2 F1 E1
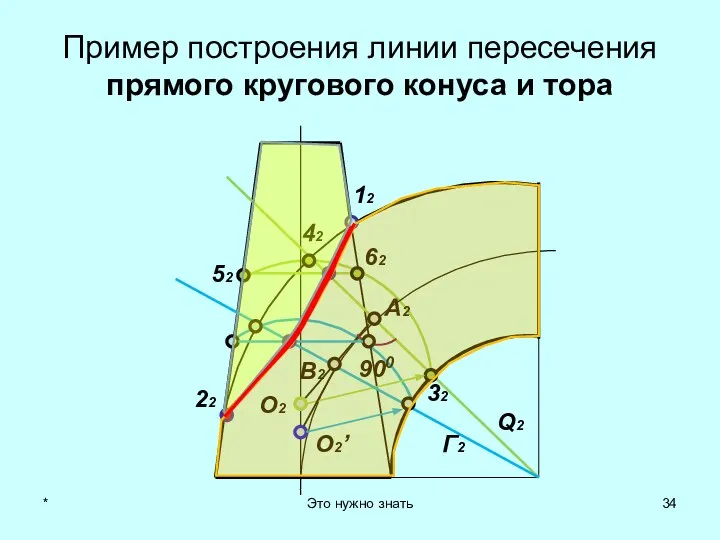
- 34. 12 22 Q2 A2 900 O2 42 32 62 52 Г2 В2 O2’ Пример построения линии
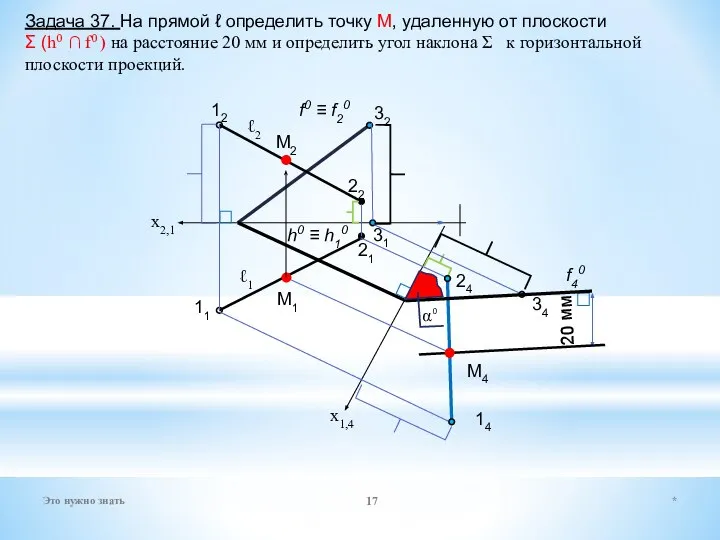
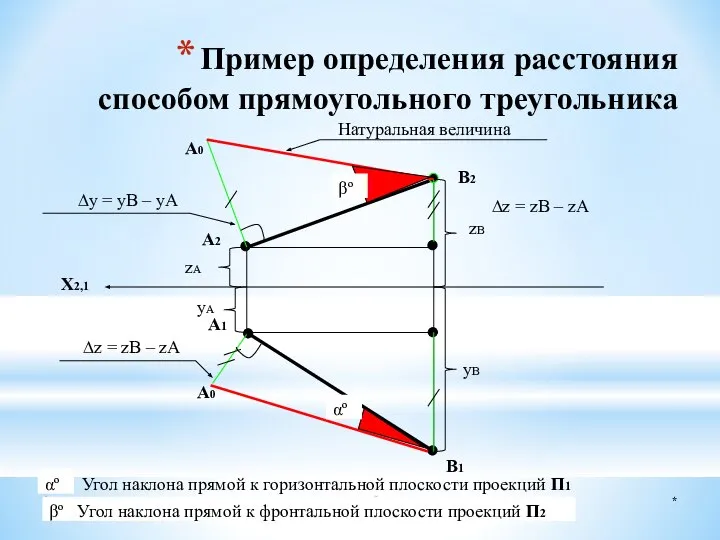
- 35. * Это нужно знать Пример определения расстояния способом прямоугольного треугольника X2,1 A2 B2 B1 A1 A0
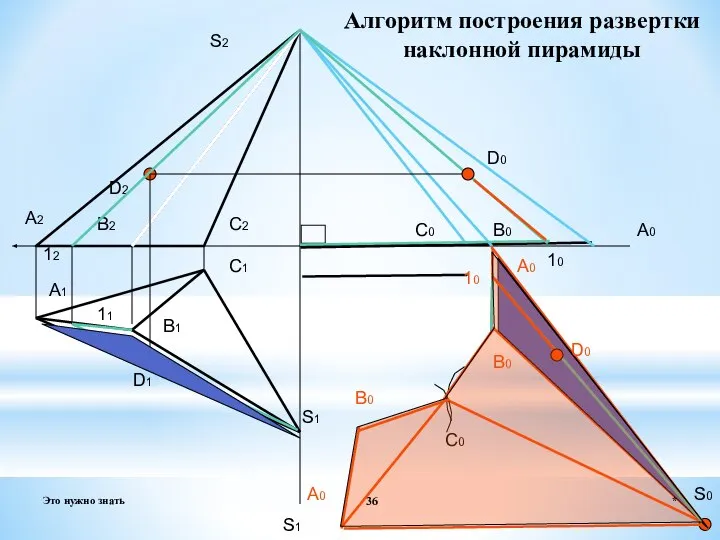
- 36. S2 S1 А1 B1 C1 А2 B2 C2 А0 C0 B0 S0 А0 C0 B0 А0
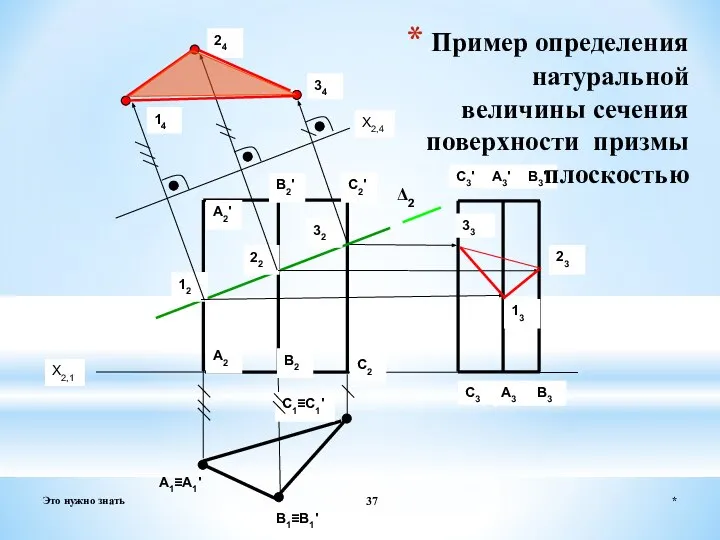
- 37. X2,1 А1≡А1' В1≡В1' С1≡С1' С2 В2' В2 А2 А2' С2' В3' С3' А3' А3 В3 С3
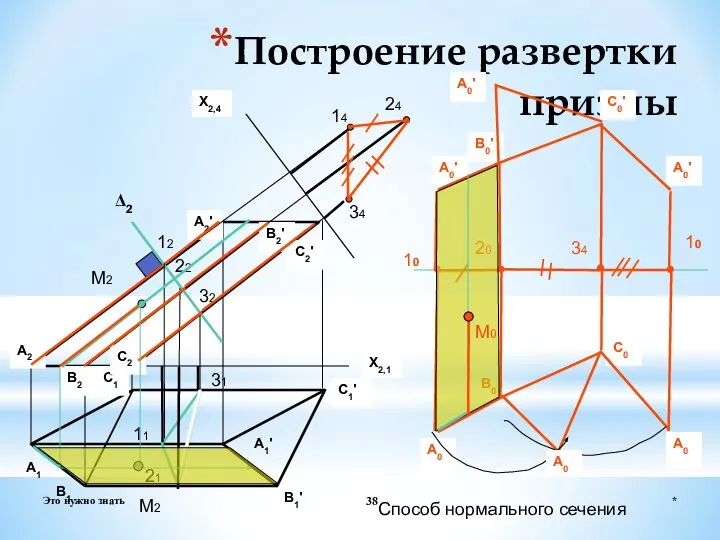
- 38. * Это нужно знать Построение развертки призмы Δ2 X2,1 А1 В1 С1 С2 В2' В2 А2
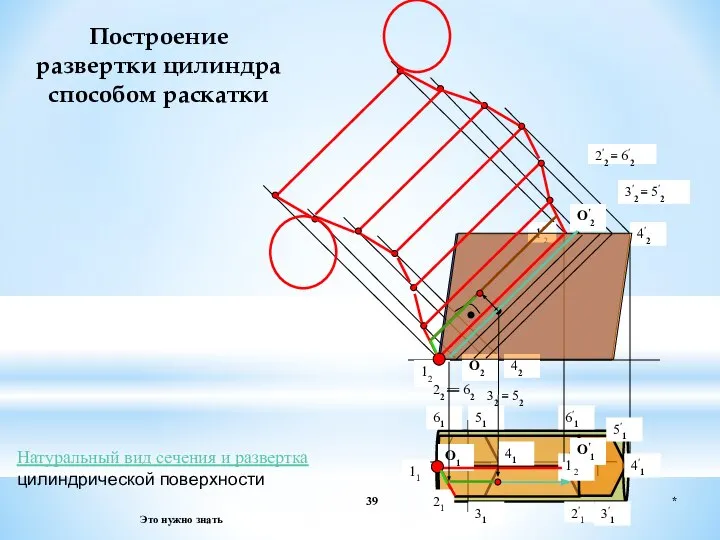
- 39. * Это нужно знать Построение развертки цилиндра способом раскатки 12 42 1′2 4′2 O2 O′1 O′2
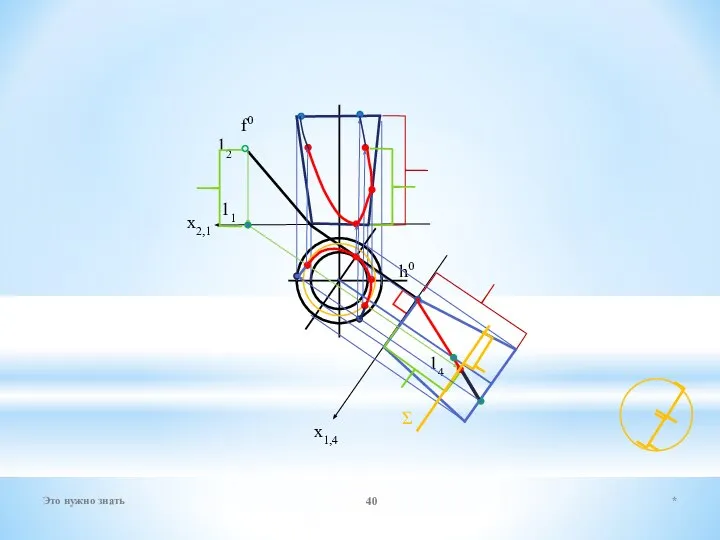
- 40. * Это нужно знать h0 f0 х2,1 х1,4 12 11 14 Σ
- 41. 3. Прямые и плоскости, касательные к поверхностям. (С графическими пояснениями). Рассмотрим примеры построения касательных плоскостей к
- 43. Скачать презентацию











 Урок математикив 4 классе МБОУ СОШ № 8 г. Туапсе
Урок математикив 4 классе МБОУ СОШ № 8 г. Туапсе Introduction
Introduction TUV NORD CERT GmbH
TUV NORD CERT GmbH Стратегический менеджмент
Стратегический менеджмент Единый государственный экзамен: итоги и перспективы 2010-2011
Единый государственный экзамен: итоги и перспективы 2010-2011 Слава русского оружия
Слава русского оружия Абсолютная гармония !
Абсолютная гармония ! ИЗО
ИЗО Блок-схема от нашей группы на тему: Порядок образования сельскохозяйственного кооператива
Блок-схема от нашей группы на тему: Порядок образования сельскохозяйственного кооператива Методика обучения иностранным языкам
Методика обучения иностранным языкам Технология изготовления изделий из текстильных и нетканых материалов ручным способом
Технология изготовления изделий из текстильных и нетканых материалов ручным способом chto_izuchaet_kurs_obzh
chto_izuchaet_kurs_obzh ЕГЭ по Обществознанию
ЕГЭ по Обществознанию Основные понятия научной дисциплины
Основные понятия научной дисциплины Проектирование учебного процесса по физике на основе педтехнологии В.М. Монахова
Проектирование учебного процесса по физике на основе педтехнологии В.М. Монахова Строение пылевых комплексов, связанных со спутниками планет Орлов С.А. Научно-исследовательский астрономический институт им. В. В.
Строение пылевых комплексов, связанных со спутниками планет Орлов С.А. Научно-исследовательский астрономический институт им. В. В.  Формирование, ведение и использование федерального и регионального учета пуль, гильз и патронов со следами нарезного ручного
Формирование, ведение и использование федерального и регионального учета пуль, гильз и патронов со следами нарезного ручного «у семи нянек дитя без глазу…»или кто должен лечить больного сахарным диабетом 2 типа
«у семи нянек дитя без глазу…»или кто должен лечить больного сахарным диабетом 2 типа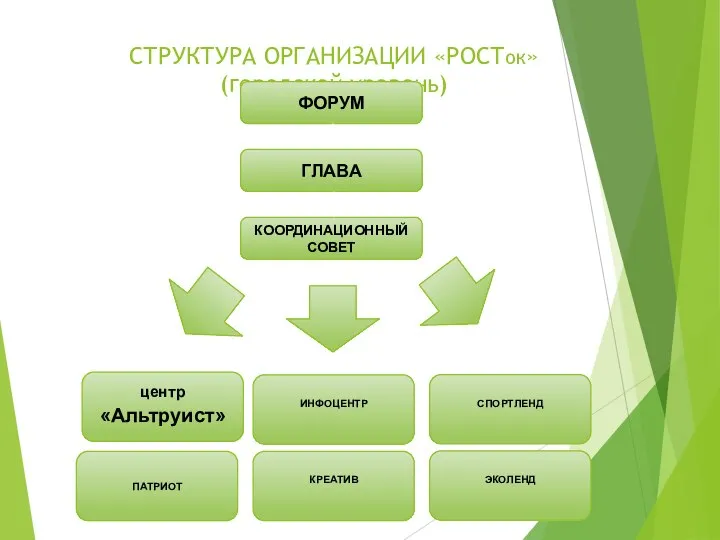 Структура организации РОСТок
Структура организации РОСТок Описание областей влияния базисных вейвлет-функций при помощи ИТ и построение решения задачи Дирихле для некоторых специальных о
Описание областей влияния базисных вейвлет-функций при помощи ИТ и построение решения задачи Дирихле для некоторых специальных о Пейзаж и его разновидности
Пейзаж и его разновидности Основы параллельного программирования с использованием MPI Лекция 1
Основы параллельного программирования с использованием MPI Лекция 1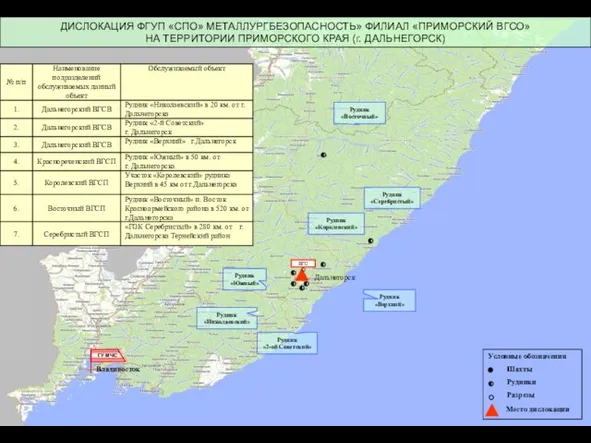 ДИСЛОКАЦИЯ ФГУП «СПО» МЕТАЛЛУРГБЕЗОПАСНОСТЬ» ФИЛИАЛ «ПРИМОРСКИЙ ВГСО» НА ТЕРРИТОРИИ ПРИМОРСКОГО КРАЯ (г. ДАЛЬНЕГОРСК)
ДИСЛОКАЦИЯ ФГУП «СПО» МЕТАЛЛУРГБЕЗОПАСНОСТЬ» ФИЛИАЛ «ПРИМОРСКИЙ ВГСО» НА ТЕРРИТОРИИ ПРИМОРСКОГО КРАЯ (г. ДАЛЬНЕГОРСК) Презентация объекта. Красная поляна
Презентация объекта. Красная поляна Презентация на тему Различие на письме частиц НЕ и НИ
Презентация на тему Различие на письме частиц НЕ и НИ Памятник Петру Великому "Медный всадник"
Памятник Петру Великому "Медный всадник" http://vkontakte.ru/club13752538
http://vkontakte.ru/club13752538 Картина М.В. Нестерова
Картина М.В. Нестерова