през Л5

Унификация уравнений движения
Упростить запись динамических уравнений движения:
dpk/dt = - ∂U/∂qk
Здесь НОВАЯ НУМЕРАЦИЯ:
qk - ∀ из 3N координат системы МТ,
pk – соответствующая ей проекция импульса.
Еще упрощения:
K = Σ Ki = ½Σpi2/mi = ½Σ(pxi2 + pyi2 + pzi2)/mi = = ½Σpk2/mk
Индексы i перебирает все МТ, а k – все координаты. После дифференцирования по компонентам импульса:
∂K/∂pk = ½.2pk/ mk = vk = dqk/dt

Уравнения Лагранжа

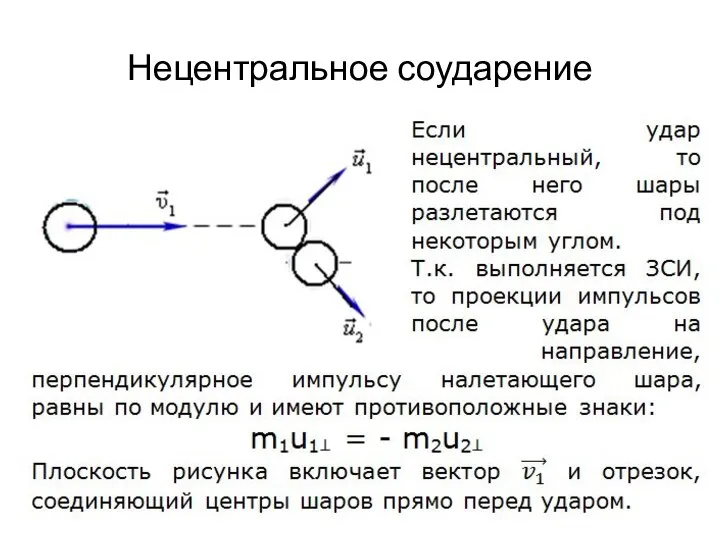
Задача о столкновении 2 шаров (МТ)

Центральное упругое соударение

Центральные неупругие соударения

Центральные неупругие соударения
ЗСЭ точно выполняется редко. Часть энергии обычно уходит на нагрев тел (частично упругий удар).
В ЛЧ второго уравнения появляется множитель q< 1:
½m1v12 . q = ½m1u12 + ½m2u22
Выражения для u1 и u2 усложнятся, но главная трудность в том, что q заранее не известен.
Второй крайний случай - абсолю́тно неупру́гий удар, в рез-те кот. скорости шаров становятся после удара равными, шары двигаются вместе (слиплись):
u1 = u2 = u
В этом случае: u = m1 v1/(m1 + m2)

Нецентральное соударение

Движение вблизи потенциального барьера или ямы (1)

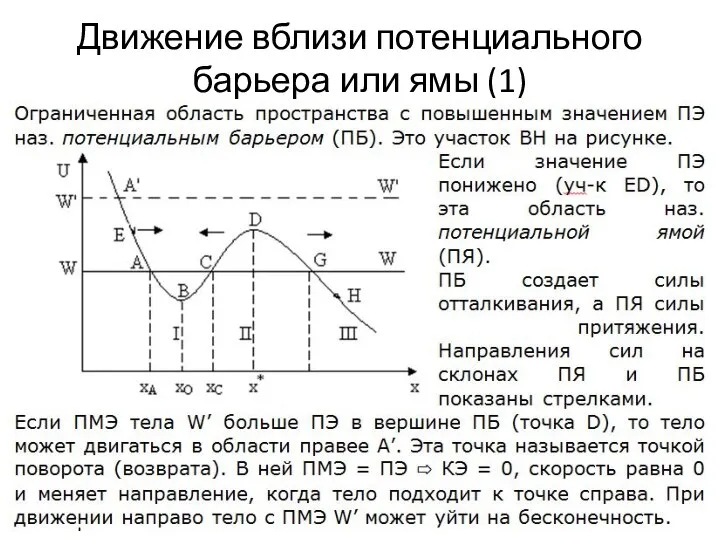
Движение вблизи потенциального барьера или ямы (2)

Момент импульса

Момент силы

Уравнение моментов

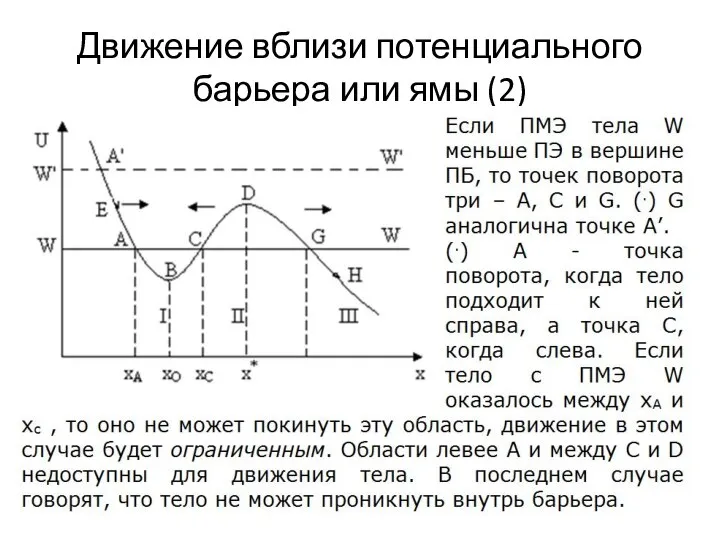
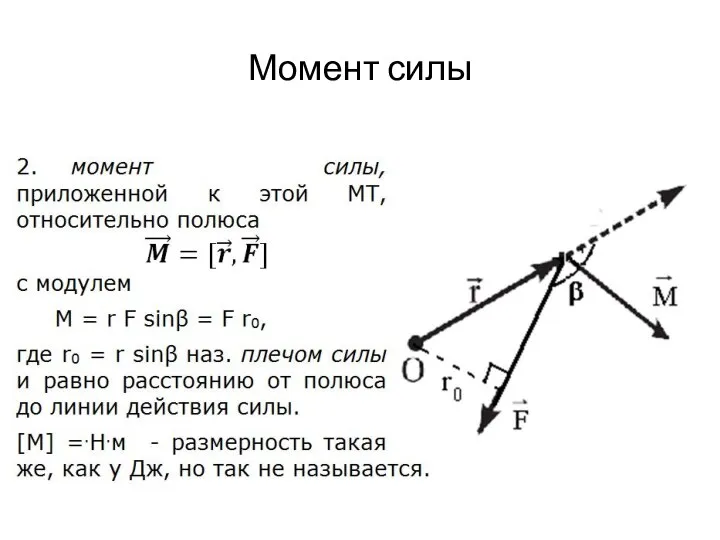
Уравнение моментов и законы Кеплера

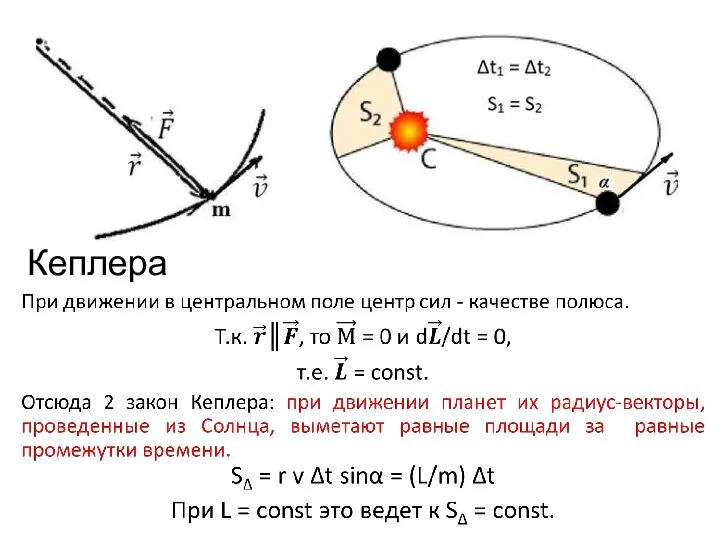
Уравнение моментов для системы МТ

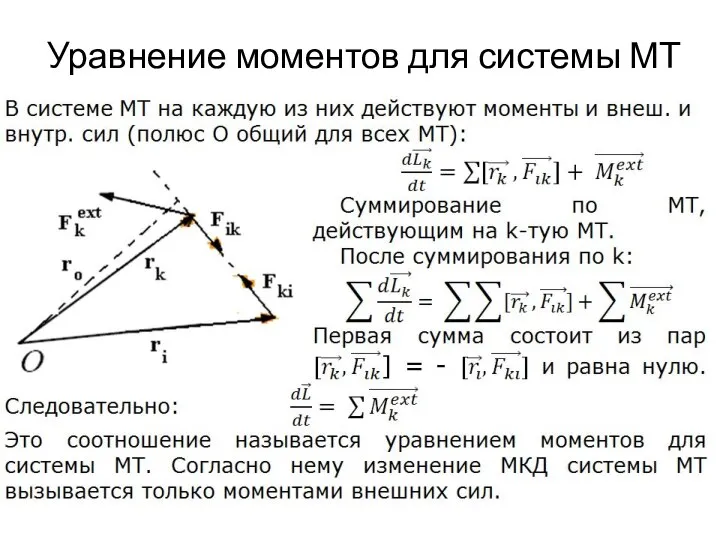
Закон сохранения момента импульса