Калабергенова Жанна 10 «Б» класс Ц.О. № 1048 г. Москвы.2011

1)D(f)=R-функция целая рациональная
2)Ф - я нечетная,т.к.
f(-x)=1/3(-x)-(-x)^3=-1/3x+x^3=-f(x)

Точки пересечения с осями координат
3)ох:1/3x-x^3=0
x=0или x≈0,6 или х ≈-0,6
oy : y=0

f’=1/3-3x^2
1)D(f’)=R=D(f);критических точек, в которых f’ не существует, нет
2)Находим критические точки в которых f’=0
1/3-x^3=0
x=±1/3
3) f’(-10)= -296
f’
f’(10)=-996

1)Находим max и min функции
f(1/3)=1/3 x1/3-(1/3)^3=
1/9-1/27=3/27-1/27≈0,07;
Т.к ф-я нечетная: f(-1/3)=-0,07

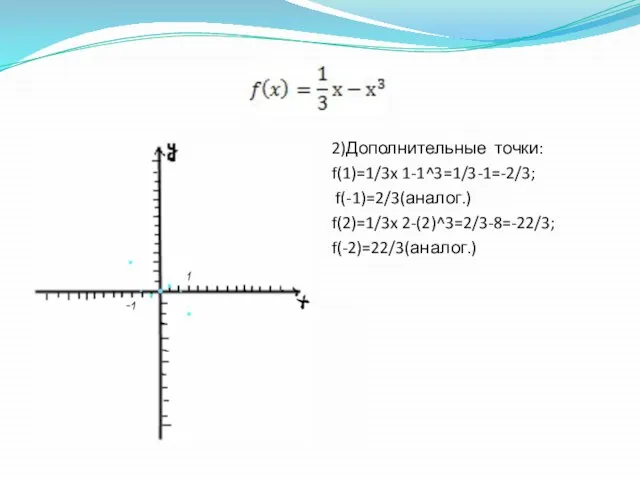
2)Дополнительные точки:
f(1)=1/3x 1-1^3=1/3-1=-2/3;
f(-1)=2/3(аналог.)
f(2)=1/3x 2-(2)^3=2/3-8=-22/3;
f(-2)=22/3(аналог.)