Содержание
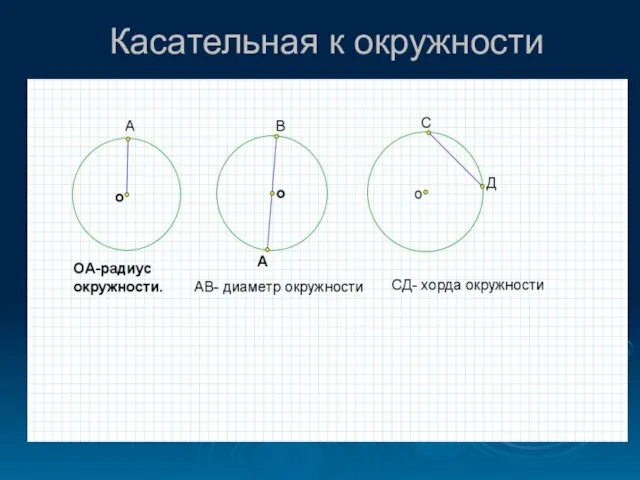
- 2. Касательная к окружности
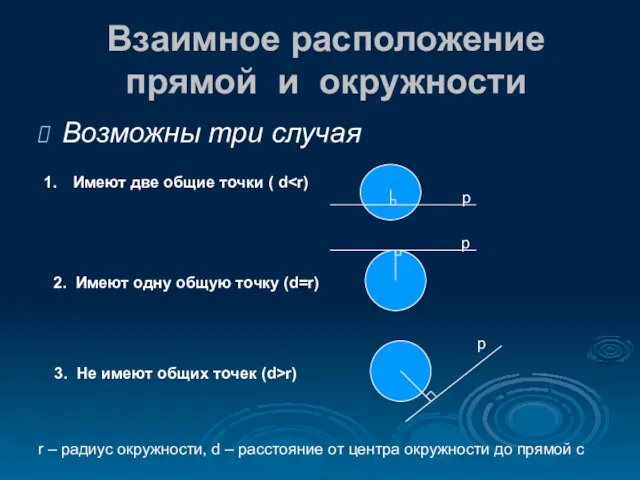
- 4. Взаимное расположение прямой и окружности Возможны три случая Имеют две общие точки ( d 2. Имеют
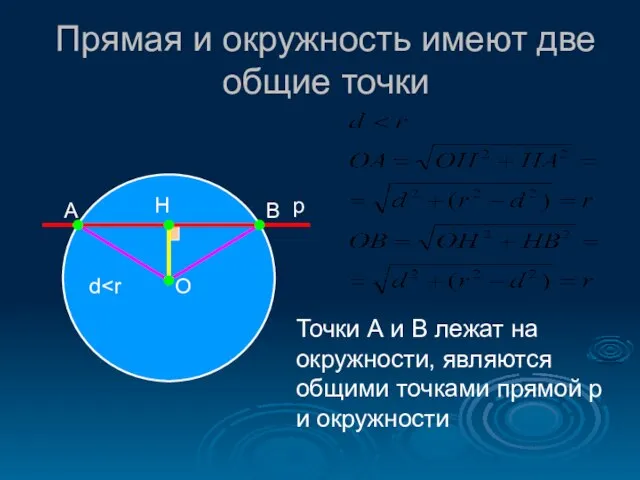
- 5. Прямая и окружность имеют две общие точки А В О Н p Точки А и В
- 6. Прямая и окружность имеют одну общую точку d=r OH=r Точка Н лежит на окружности и является
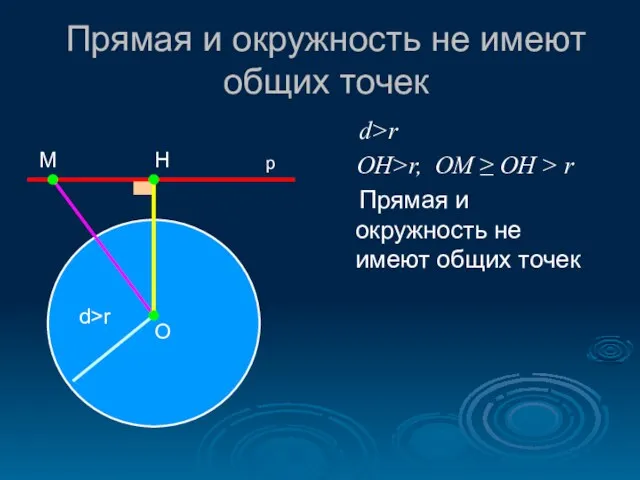
- 7. Прямая и окружность не имеют общих точек d>r OH>r, OM ≥ OH > r Прямая и
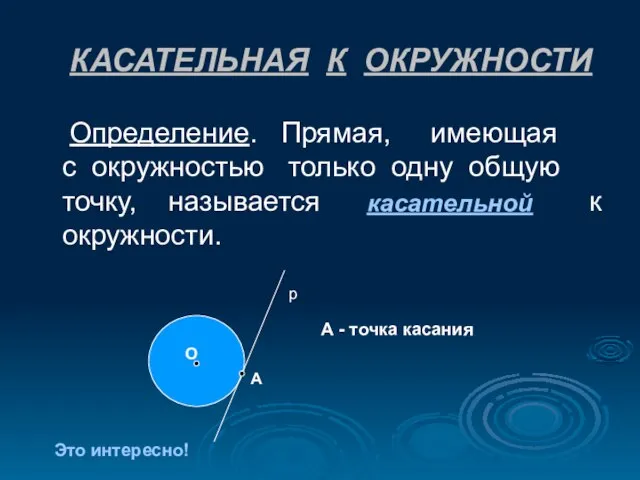
- 8. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ Определение. Прямая, имеющая с окружностью только одну общую точку, называется к окружности. А
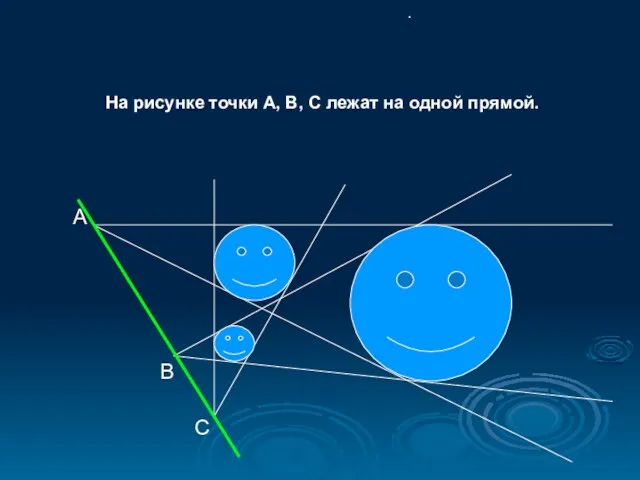
- 9. А С В На рисунке точки А, В, С лежат на одной прямой. .
- 10. (О свойстве касательной) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания . 1.Пусть р
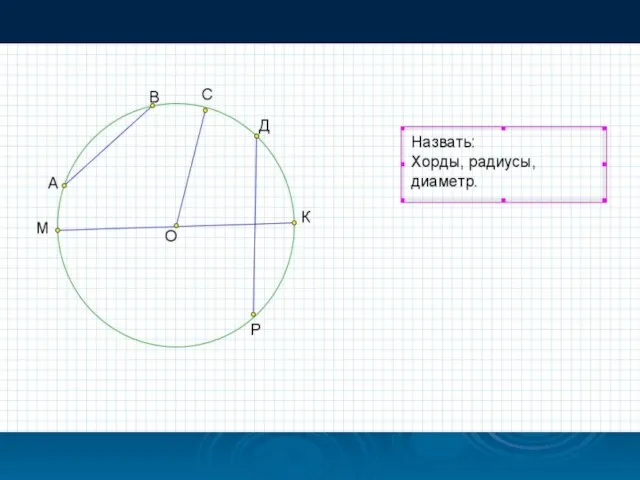
- 11. Каким может быть взаимное расположение прямой и окружности? Как называется прямая, которая имеет с окружностью две
- 12. № 631 а) d б) d > r, прямая и окружность не имеют общих точек, д)
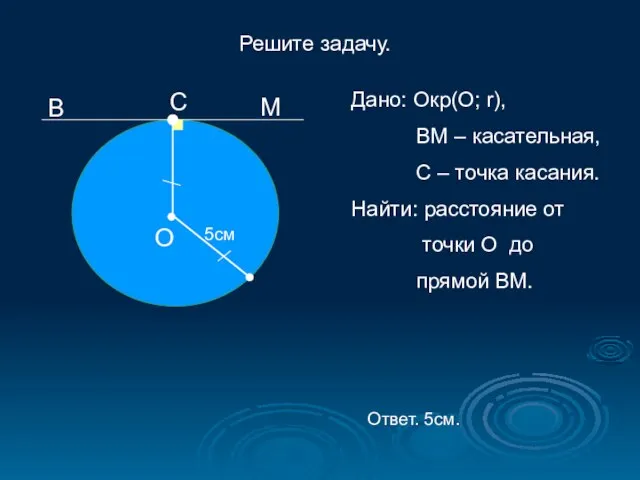
- 13. Решите задачу. В М О 5см Дано: Окр(О; r), ВМ – касательная, С – точка касания.
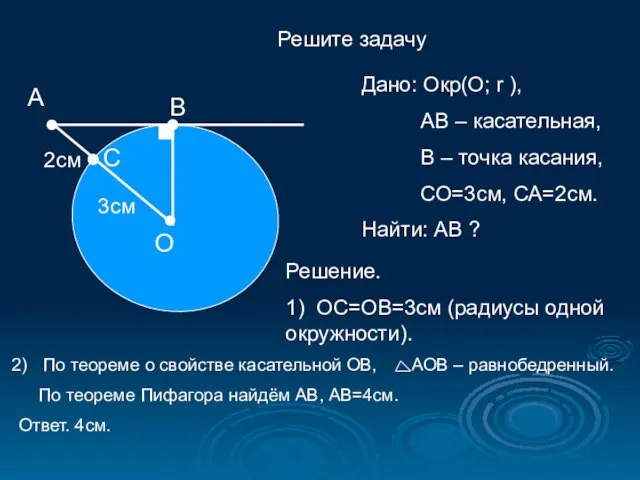
- 14. Решите задачу А О В С 3см 2см Дано: Окр(O; r ), АВ – касательная, В
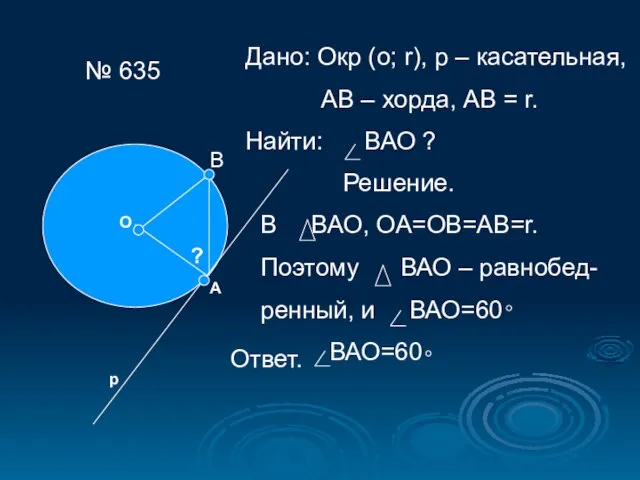
- 15. № 635 О А р ? Дано: Окр (о; r), р – касательная, АВ – хорда,
- 16. Домашнее задание №631(в.г) №634 Итоги урока.
- 18. Скачать презентацию





 МОУ "Вурнарская СОШ №1"
МОУ "Вурнарская СОШ №1" информационные ресурсы
информационные ресурсы Эффективность принятия управленческих решений
Эффективность принятия управленческих решений Религия как одна из форм культуры
Религия как одна из форм культуры Философия Возрождения и Нового времени
Философия Возрождения и Нового времени Сказ об 11 А классе
Сказ об 11 А классе Технологии дистанционного обучения. Электронный учебник. Контрольно-кассовые машины. Введение
Технологии дистанционного обучения. Электронный учебник. Контрольно-кассовые машины. Введение Подвиды темпераментов
Подвиды темпераментов Презентация на тему Россия в начале 20 в
Презентация на тему Россия в начале 20 в  ПРЕЗЕНТАЦИЯ
ПРЕЗЕНТАЦИЯ Sootnoshenie_nauchnoy_i_uchebnoy_poznavatelnoy_deyatelnosti
Sootnoshenie_nauchnoy_i_uchebnoy_poznavatelnoy_deyatelnosti Роль домашних заданий в учебной деятельности школьника при подгтовке к ГИА и ЕГЭ в средней школе
Роль домашних заданий в учебной деятельности школьника при подгтовке к ГИА и ЕГЭ в средней школе Таинственные камни
Таинственные камни Создание информационной системы управления инвестиционной деятельностью и капитальным строительством ОАО «МОЭСК»
Создание информационной системы управления инвестиционной деятельностью и капитальным строительством ОАО «МОЭСК» Начало начал
Начало начал Методы исследования
Методы исследования Кадастр антропогенных выбросов парниковых газов для г. Москвы (сектор «Энергетика»)
Кадастр антропогенных выбросов парниковых газов для г. Москвы (сектор «Энергетика») Пространственные отношения: слева - справа, выше – ниже, вверху – внизу, перед – за, между, над – под.
Пространственные отношения: слева - справа, выше – ниже, вверху – внизу, перед – за, между, над – под. Химические элементы
Химические элементы "Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов)
"Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов) Презентация на тему Публичное выступление
Презентация на тему Публичное выступление  Об условиях эффективного использования финансовых средств модернизации муниципальных образовательных систем
Об условиях эффективного использования финансовых средств модернизации муниципальных образовательных систем Село сибирское – Бакчар
Село сибирское – Бакчар Найди лишний предмет
Найди лишний предмет Декабристы В Сибири
Декабристы В Сибири Let's save our fragile planet
Let's save our fragile planet How Do I know the Bible?
How Do I know the Bible? Подключение к Интернету
Подключение к Интернету