Kinematics

Some definitions
Reference systems (frame)
Reference system (frame) that is coordinates system jointly with watch for time measurement. Reference system defines the the space and time characteristics of body position. Space position is given by coordinates system, time position is given due to time measurement using watch.
Mechanical motion
That is change of mutual position of bodies one with respect another in the space during a time.много расположения тел
Any mechanical motion has relative character.о.
Material particle
that is physical body which has negligible dimensions and form in comparison with dimensions of other bodies or distance to them at conditions of problem under consideration.

1.1. Position vector of material particle
Motion of material particle M can be considered in Cartesian frame with origin at the point O using coordinates of particle x, y, z.
are the unit vectors of coordinate axes.
Position vector
defines the position of particle M in the given coordinate system.
Modulus of position vector is

1.2.Kinematic equations of particle motion
The change of coordinates particle in time can be written by 3 scalar equations
or by one vector equation for position vector as function of time:

1.3. Trajectory of material article
Trajectory is the line which presents the imaginary track of particle at its motion in the space.
Kinematics equations includes the trajectory in the parametric form (time t is a parameter): x = f1(t); y = f2(t); z = f3(t).
After exclusion of time trajectory equation has the form of curvilinear line equation in the space of coordinate system: y = F(x).

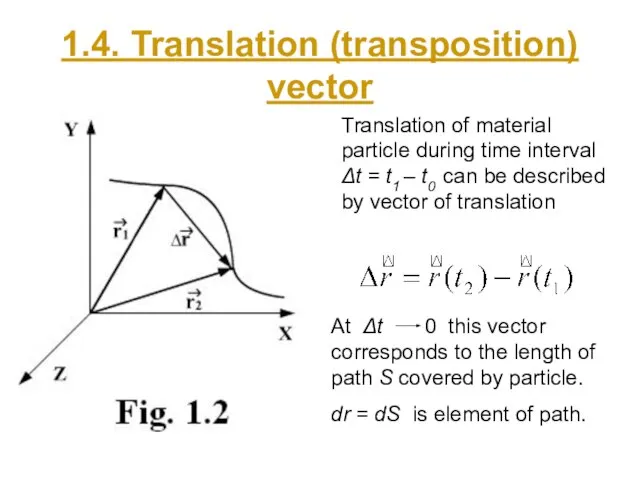
1.4. Translation (transposition) vector
Translation of material particle during time interval Δt = t1 – t0 can be described by vector of translation
At Δt 0 this vector corresponds to the length of path S covered by particle.
dr = dS is element of path.

1.5. Velocity of motion
M is position of particle at time instant t1 .
N is position of particle at time instant t2 .
Vector of mean velocity during time interval Δt = t2 – t1 is
Vср= ΔS/Δt
This vector is directed along MN.
Instantaneous velocity is a vector defined at Δt 0, and directed tangentially:

Addition of velocities
The particle can take part in different motion simultaneously.
At
the resulting velocity is a vector sum of velocity values for all elementary components of motion:

1.6. Acceleration (tangential and normal)
Average acceleration during time interval Δt is a vector
Tangential acceleration
Total acceleration
At
At Δφ 0 B D, BC CD; CD/MC = MM1/OM1;
vn = vτ ΔS/R
Normal acceleration

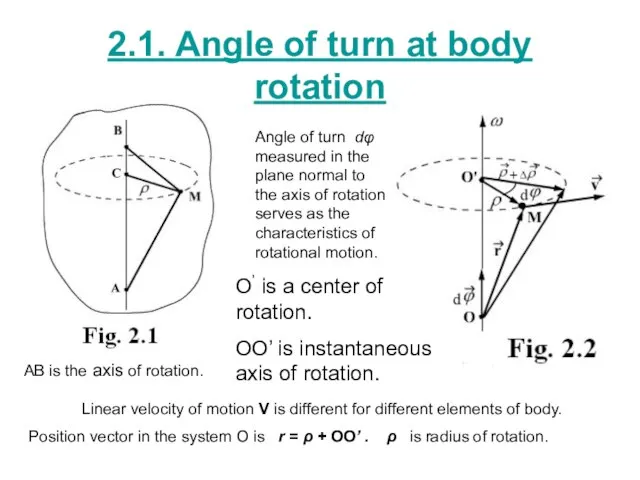
2.1. Angle of turn at body rotation
AB is the axis of rotation.
Angle of turn dφ measured in the plane normal to the axis of rotation serves as the characteristics of rotational motion.
Ο’ is a center of rotation.
OΟ’ is instantaneous axis of rotation.
Linear velocity of motion V is different for different elements of body.
Position vector in the system O is r = ρ + ΟΟ’ . ρ is radius of rotation.

2.2. Angular velocity
Angular velocity ω is an axial vector. Its direction is defined by rule of right screw.
Uniform rotation:
At uniform rotation the angular velocity shows the angle of body turn per unit of time.
T is a period of rotation;
f is a frequency of rotation.

2.4. Angular acceleration
At non-uniform rotation the change of angular velocity per unit of time gives the angular acceleration ε :
Orientation of axial vectors ω, ε along axis of rotation:
Rotation with acceleration
b) Rotation with breaking
At the rotation with constant angular acceleration
ε = Δω/Δt =Δφ/(Δt)2

2.5. Correlation of linear and angular parameters of motion
Path of displacement for elementary particle of body during rotation
ΔS = R Δφ
Normal acceleration
Tangential acceleration

3.1.Mechanical force. Moment of force. Momentum of material particle.
Resulting force F on the body is the vector sum of all forces applied to the body
Moment of force (імпульс сили) is
dp = F dt
Momentum of material particle or body is
(імпульс тіла = кількість руху)

3.2. Newton’s Laws
1st Newton’s Law: Any physical body saves the state of rest or uniform motion while other bodies do not change this state by their action on the body.
2nd Newton’s Law (main law of dynamics for mechanical motion):
Here
is a mechanical momentum of material particle.
For body of constant mass this law has the view
Independent action of forces on the body:
Mass m defines the inertial properties of body.

3.3. Third Newton’s Law
Two material particles interact one with ahother with forces which have the equal values and are directed in opposite sides along the line connecting these particles.
Important: these forces are applied to different bodies that is why they cannot compensate one another

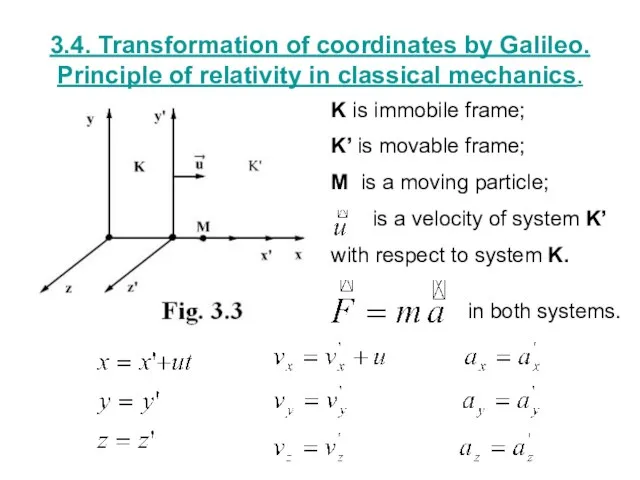
3.4. Transformation of coordinates by Galileo.
Principle of relativity in classical mechanics.
K is immobile frame;
K’ is movable frame;
M is a moving particle;
is a velocity of system K’
with respect to system K.
in both systems.

3.5. Principle of relativity by Galileo
Uniform motion of closed system with respect some inertial frame has no influence on the laws of mechanical motion inside of the moving system.
Newton’ laws are invariant for Galileo transformation of coordinates.
Newton’s laws for material particle as well as for any assembly of particles are true and are the same at any inertial frame.

3.6. A center of mass (center of inertia) for system of material particles
Any physical body can be represented as aggregation of totality big number (n) of elementary particles. The motion of body in whole can be described as motion of the center of mass which position is introduced by correlation

3.7. Velocity and momentum of body
using the center of mass
The components of position vector for center of mass:
Velocity for center of mass
Total Momentum for system of particles

3.8. Equation of dynamics for translational motion of solid
From
and
we have
or
, where
Momentum conservation law for closed system of particles
and
, so
As

4.1. Mechanical Work and Power
When some force F = i Fτ + j Fn moves a body, the value A= FcosαS is a work of force on the body movement along the path S.
Elementary work is dA = Fτ dS = Fτ vdt.
Fτ = Fcosα is the component of vector force along direction of motion (v).
Power is a work done per unit of time:
N = dA/dt = Fτ v.

4.2. Kinetic energy WK = mv2 /2
(this term was proposed first by scientist Coriolis)
Using the 2nd Newton’s Law we can write
Integration along the path from 1 up to 2 yields to next:
leads to
, where
is change of kinetic energy WK ;
A21 is a full work of forces between points 1 and 2.
, what

4.3. Potential field and forces in this field
The force field is potential field if the work for the mass movement from point 1 to point 2 does not depend on the path trajectory.
In general a potential energy of field WP can depend on the coordinates x, y, z.
The components of force are given by derivatives
In the vector form
The vector function

4.4. Energy conservation law
During motion of body in the potential field ΔΑ = ΔWK and ΔA = - ΔWP . Thus
ΔWK = - ΔWP . Δ(WK + WP ) = 0.
E = WK + WP = const.
A total energy E for closed system of bodies is constant at all processes and transformations.

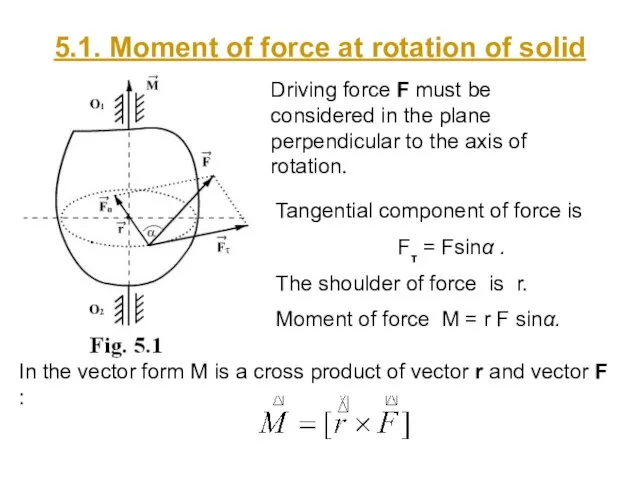
5.1. Moment of force at rotation of solid
Driving force F must be considered in the plane perpendicular to the axis of rotation.
Tangential component of force is
Fτ = Fsinα .
The shoulder of force is r.
Moment of force M = r F sinα.
In the vector form M is a cross product of vector r and vector F :

5.2.Moment of inertia for material particle at circular motion
For material particle moving along the circular orbite it is possible to write
Taking into account
and
we have
In the vector form
is a moment inertia for material particle at the circular orbite
is the main law of rotational motion for material particle

5.3. Moment inertia of solid
When material of solid has non-unifom density along the volume, moment of inertia is calculated as
Moment of inertia for solid can be calculated as sum of moments of inertia for all elements of its mass (or its volume):
Here