Классическое определение вероятности

Всё в природе подлежит измерению, всё может быть сосчитано
Н.И. Лобачевский

Николай Иванович Лобачевский
Русский математик
Один из создателей неевклидовой геометрии
Ректор Казанского университета
1792 – 1856

Детерминизм
осуществление определённых условий однозначно определяет результат

Блез Паскаль
Французский математик, механик, физик, литератор и философ
Один из создателей математического анализа, теории вероятностей и проективной геометрии
1623 – 1662

Пьер Ферма
Французский математик
Один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел
1601 – 1665

Христиан Гюйгенс ван Зёйлихем
Нидерландский математик, механик, физик, астроном и изобретатель
Один из создателей теоретической механики и теории вероятностей
1629 – 1695

Испытание
Эксперимент, результат которого заранее (до проведения) предугадать нельзя
Испытание = опыт =
= стохастический эксперимент

Случайное событие
Явление, которое может произойти или не произойти в результате проведения испытания
Пример
Бросание игральной кости

Случайное событие
Обозначаются большими латинскими буквами, снабжёнными иногда индексами или штрихами
Пример
Событие А = «При бросании игральной кости выпало число 3»

Элементарные события
Взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий
Каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А

Пример
Испытание – бросание игральной кости
Элементарные события – появление любого числа от 1 до 6
Всего 6 элементарных событий

Элементарные события
Обозначаются греческой буквой
ω (омега)
возможно, с индексами
Элементарное событие =
= элементарный исход

Пример
Испытание – бросание игральной кости
ω1 = «При бросании игральной кости выпало число 1»
ω4 = «При бросании игральной кости выпало число 4»

Пространство элементарных событий
Совокупность всех элементарных событий данного опыта
Ω (омега)

Пространство элементарных событий
Совокупность всех элементарных событий данного опыта
Ω (омега)

Пример
Испытание – бросание игральной кости
Пространство элементарных событий состоит из шести событий
Ω = {ω1, ω2, ω3, ω4, ω5, ω6}

Благоприятные события
Элементарные события, наступление которых необходимо влечёт наступление события А
Для каждого события А – свои благоприятные события!

Благоприятные события
А – множество элементарных событий, благоприятных событию А
А ⊆ Ω
Отождествляем событие А и множество А

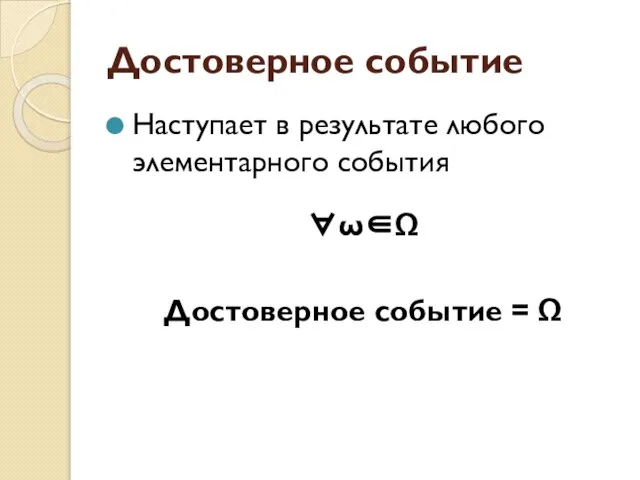
Достоверное событие
Наступает в результате любого элементарного события
∀ω∈Ω
Достоверное событие = Ω

Невозможное событие
Не наступает ни при каком элементарном событии
Невозможное событие = ∅

Пример
Испытание – бросание игральной кости
А = «Выпало число, меньшее 7»
А = Ω
В = «Выпало отрицательное число»
В = ∅

Сумма событий
А + В − событие, которое происходит ⇔ происходит хотя бы одно из событий А или В
А + В = А ∪ В
Сумма событий =
= объединение событий

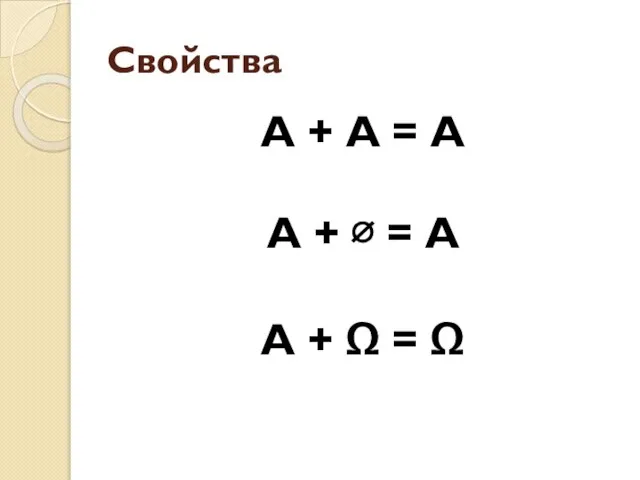
Свойства
А + А = А
А + ∅ = А
А + Ω = Ω

Пример
Испытание – бросание игральной кости
А = «Выпало чётное число»
А1 = «Выпало число 2»
А2 = «Выпало число 4»
А3 = «Выпало число 6»
А = А1 + А2 + А3

Произведение событий
А×В − событие, которое происходит ⇔ происходят оба события А и В
А×В = А ∩ В
Произведение событий =
= пересечение событий

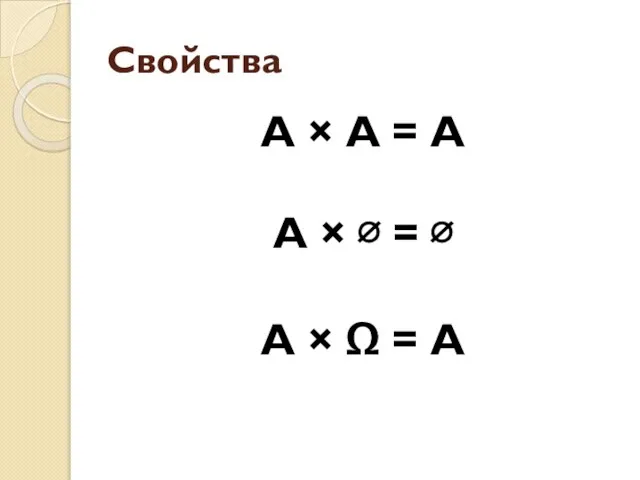
Свойства
А × А = А
А × ∅ = ∅
А × Ω = А

Пример
Испытание – бросание игральной кости
В = «Выпало число 5»
В1 = «Выпало нечётное число»
В2 = «Выпало число, большее 3»
В = В1×В2

Несовместные события
Одновременное появление в опыте невозможно
А×В =∅
Иначе – совместные события

Пример
Испытание – бросание игральной кости
А = «Выпало чётное число»
В = «Выпало нечётное число»
А и В несовместны

Противоположное событие
Происходит ⇔ не происходит событие А
¬А

Свойства
¬ А× А = ∅
А + ¬ А = Ω
¬ (¬ А) = А

Пример
Испытание – бросание игральной кости
А = «Выпало чётное число»
В = «Выпало нечётное число»
А и В противоположные

Разность событий
А \ В − событие, которое происходит ⇔ происходит событие А и не происходит событие В
¬ А = Ω \ А
А \ В = А ׬В

Свойства операций
А+В = В + А
А×В = В × А
А (В + С) = АВ + АС
А (ВС) = (АВ)С

Пример
Производится два выстрела по цели. Событие А = «При первом выстреле было попадание в цель»
Событие В = «При втором выстреле было попадание в цель»
Событие С = «В результате двух выстрелов цель поражена»
Выразить С через А и В

Пример – решение 1
Производится два выстрела по цели. Событие А = «При первом выстреле было попадание в цель»
Событие В = «При втором выстреле было попадание в цель»
Событие С = «В результате двух выстрелов цель поражена»
Выразить С через А и В

Пример – решение 1
1) первый выстрел – попадание, второй – промах
А×(¬В)
2) первый выстрел – промах, второй – попадание
¬А×В
3) оба выстрела – попадания
А×В

Пример – решение 1
Интересующее событие наступает в результате наступления хотя бы одного из вариантов
С = А×(¬В) + (¬А)×В + А×В

Пример – решение 2
Событие ¬ С = «Поражения цели не было»
¬ С = (¬А) ×(¬В)
С = ¬(¬ С) = ¬ ((¬А) ×(¬В))
или
С =Ω \ ((¬А) ×(¬В))

Относительная частота
события А в серии из n одинаковых экспериментов
ν(А) = m(A) / n
где m(A) – число экспериментов, в которых событие А произошло

Свойства
0 ≤ ν (А) ≤ 1
ν (Ω) = 1
АВ = ∅ ⇒ ν (А+В) = ν (А) + ν (В)

Относительная частота
Меняется от серии к серии
Во многих случаях при увеличении числа опытов ν(А) приближается к некоторому числу
Это экспериментально установлено

Статистическое определение
Если при увеличении числа опытов ν(А) стремится к некоторому фиксированному числу р(А), то
событие А стохастически устойчиво,
p(А) – вероятность события А
численная характеристика

Относительная частота
события А в серии из n одинаковых экспериментов
ν(А) = m(A) / n,
где m(A) – чисто экспериментов, в которых событие А произошло

Относительная частота
события А в серии из n одинаковых экспериментов
ν(А) = m(A) / n,
где m(A) – число экспериментов, в которых событие А произошло
Всего
Благоприятные

Классическое определение
Пространство элементарных событий некоторого опыта Ω
|Ω| = n
Все элементарные события равновозможны

Классическое определение
Все элементарные события равновозможны ⇒ вероятность их появления одинакова
p(ωi) = pi = p = 1/n
p(Ω) = Σ pi = 1

Классическое определение
Пусть событию А благоприятствуют m элементарных событий
p(А) = Σ piА = m× 1/n = m/n
p(А) = m/n
Отношение числа благоприятных исходов к общему числу исходов

Пример
В урне лежит 7 жёлтых и 11 оранжевых шаров. Чему равна вероятность вытащить жёлтый шар?
Событие А = «Вытащили жёлтый шар»
Всего исходов n = 7 + 11 = 18
Благоприятных исходов m = 7
p(А) = m/n = 7/18

Пример
В ящике 10 перенумерованных шаров с номерами от 1 до 10. Вынули один шар.
Какова вероятность того, что номер вытянутого шара не превышает десяти?

Пример
Куб, все грани которого окрашены, распилен на 1000 кубиков одного размера.
Полученные кубики перемешаны. Определить вероятность того, что наудачу выбранный кубик будет иметь ровно две окрашенные грани?

Пример
В погребе в конце февраля стоит 8 банок с компотом и 7 с соленьями.
Наугад достают 6 банок.
Какова вероятность того, что одна банка будет с компотом, а остальные с соленьями?