Содержание
- 2. План доклада Что такое кластеризация и основные области её применения Этапы кластеризации, основные алгоритмы кластеризации Алгоритм
- 3. Кластеризация (кластерный анализ) “Кластерный анализ – задача разбиения заданной выборки объектов на непересекающиеся подмножества, называемые кластерами
- 4. Дистанционное зондирование Земли “Задачей классификации является перенос нагрузки по анализу и обработки информации с человека на
- 5. Анализ данных Скорой помощи
- 6. Традиционно кластеризация включает в себя следующие шаги: Определить цель исследования. Это может быть или определение кластерной
- 7. Краткий обзор методов кластеризации Классические алгоритмы Алгоритмы, основанные на минимизации функционала Алгоритм К – средних Форель(FOREL),
- 8. Алгоритм К-средних Описание алгоритма: Задание числа кластеров k, на которые надо разбить входные данные. Выбор k
- 9. Алгоритм К-средних Основная трудность, которая возникает при использовании алгоритма к-средних – необходимость задания числа кластеров. Для
- 10. Алгоритм К-средних Основные достоинства алгоритма: простота использовании метода - задание только одного параметра (числа кластеров). один
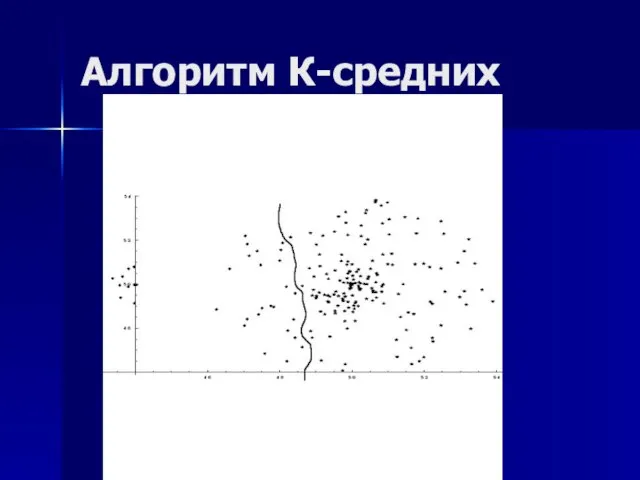
- 11. Алгоритм К-средних
- 12. Постановка задачи кластеризации Дано Требуется разбить на множество групп (кластеров) чтобы точки из одной группы были
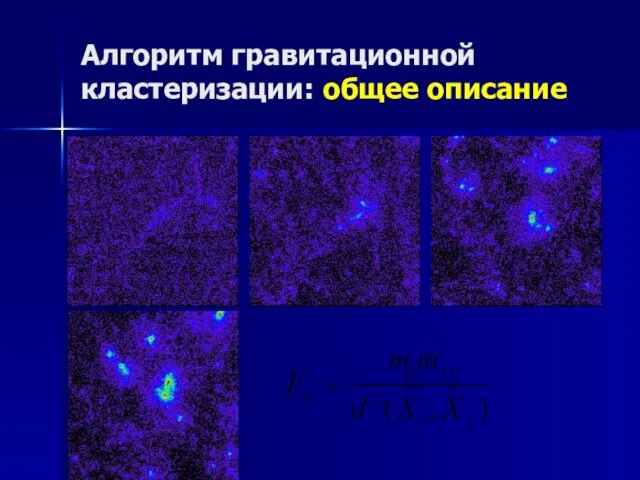
- 13. Алгоритм гравитационной кластеризации Общее описание Шаг 1: построение дерева объединений Шаг 2: построение “естественных” кластеров Шаг
- 14. Алгоритм гравитационной кластеризации: общее описание
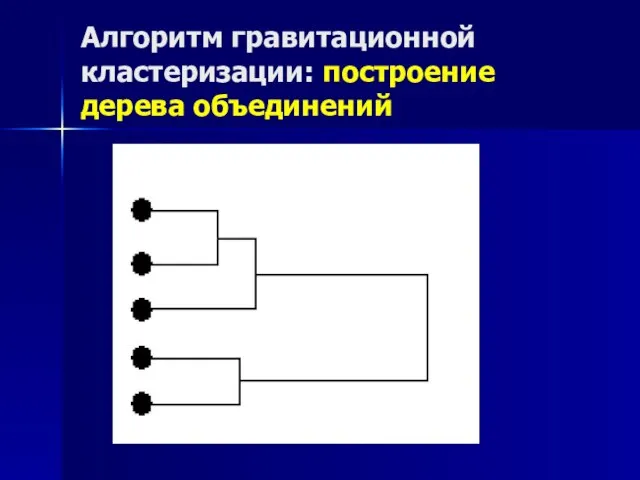
- 15. Алгоритм гравитационной кластеризации: построение дерева объединений numpoints=n; t=0; while(numpoints!=1) { объединение “близких” точек движение точек }
- 16. Алгоритм гравитационной кластеризации: построение дерева объединений
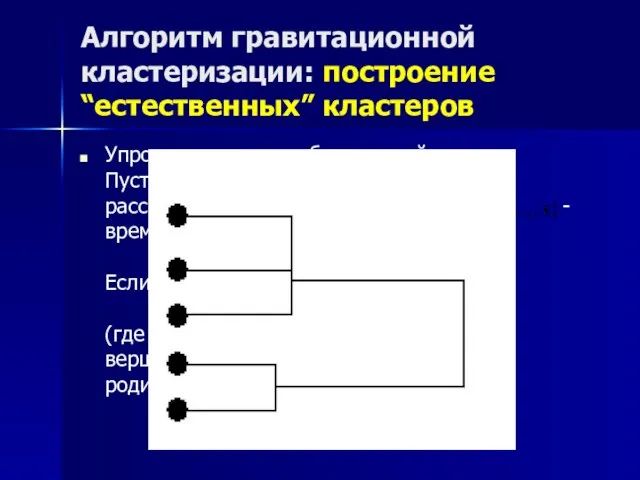
- 17. Алгоритм гравитационной кластеризации: построение “естественных” кластеров Упрощение дерева объединений Пусть - дети вершины рассмотрим величины -
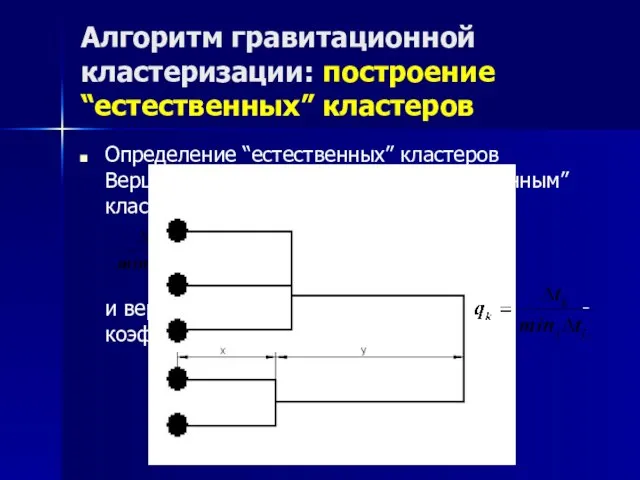
- 18. Алгоритм гравитационной кластеризации: построение “естественных” кластеров Определение “естественных” кластеров Вершину будем называть “естественным” кластером, если выполняется
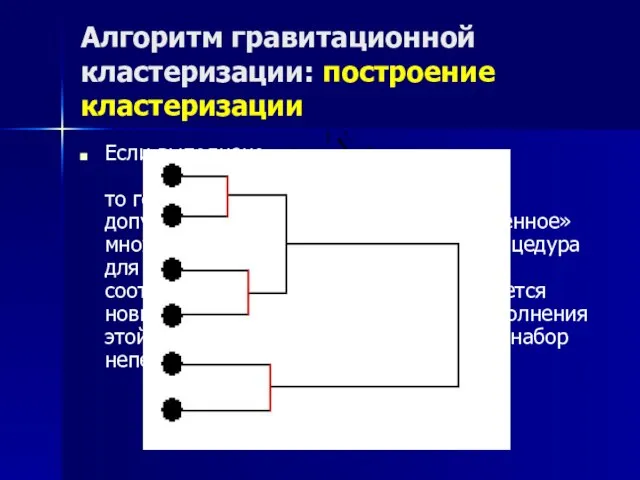
- 19. Алгоритм гравитационной кластеризации: построение кластеризации Если выполнено то говорим, что “естественный” кластер допускает разбиение на более
- 20. Достоинства Автоматическое определение числа кластеров Независимость настроек алгоритма от входных данных Дерево объединения даёт представление о
- 21. Устойчивость алгоритма гравитационной кластеризации Определение Алгоритм кластеризации устойчив на наборе данных если существуют такие что результаты
- 22. Гравитационная кластеризация по m ближайшим точкам Основная идея - учитывать влияние только m “ближайших” точек Пусть
- 23. Гравитационная кластеризация с использованием CF-дерева CF-дерево, построенное по последователь- ности из n точек с параметрами B
- 24. Модификации алгоритма гравитационной кластеризации Предложены следующие модификации алгоритма Алгоритм гравитационной кластеризации по m ближайшим точкам Алгоритм
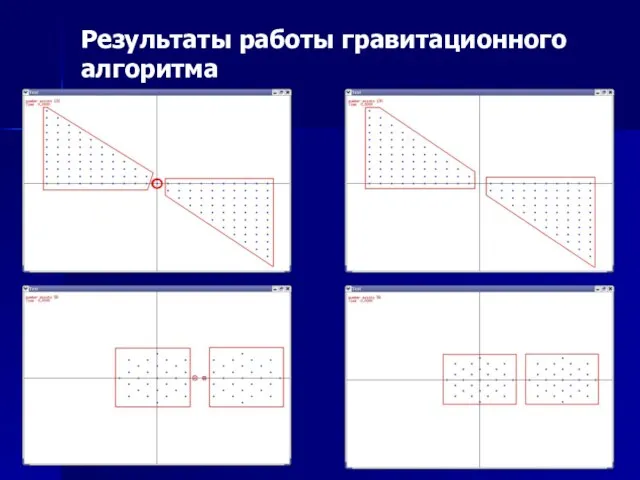
- 25. Результаты работы гравитационного алгоритма
- 26. Результаты работы гравитационного алгоритма
- 27. Области применения: обработка потоковой информации Рассматривается задача построения иерархии рубрик для системы рубрикации текстов При обучении
- 28. Области применения: обработка потоковой информации Проведенные испытания показывают, что использование дерева повышает точность определения рубрики при
- 29. Области применения: Минимизация вычислений в задаче обтекания
- 30. Минимизация вычислений в задаче обтекания Пример разбиения множества вихрей на группы Цель: разбиение множества вихрей на
- 31. Сопоставление набору точек из многомерного пространства точек на плоскости с качественным отображением: Задача визуализации 1) кластерной
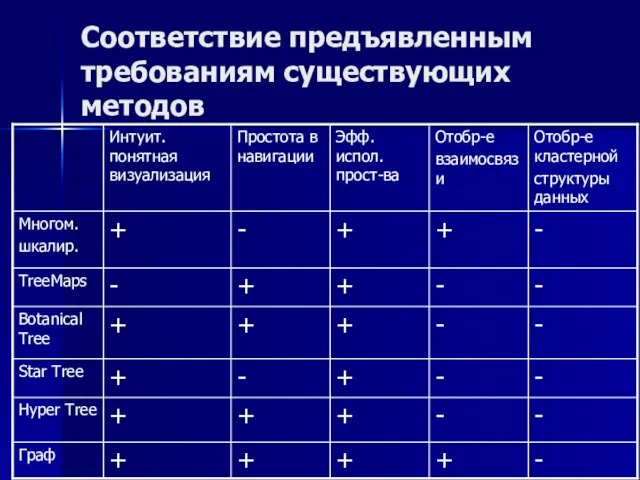
- 32. Требования к алгоритму визуализации 1) интуитивно понятное изображение 2) простота в навигации по данным 3) эффективное
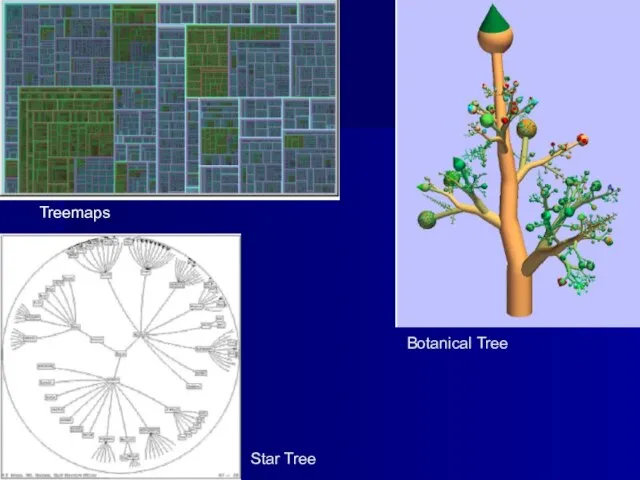
- 33. Существующие подходы 1)Многомерное шкалирование 2) TreeMaps 3) Botanical Tree 4) Star Tree 5) Hyperbolic Display 6)
- 34. Treemaps Botanical Tree Star Tree
- 35. Соответствие предъявленным требованиям существующих методов
- 36. Визуализация многомерных данных Определение Визуализация — множество где Определение Визуализатор — множество визуализаций, т.е. Число s
- 37. Дерево визуализации Каждая визуализация отображается как набор точек. Конкретное состояние визуализатора – некоторая конфигурация точек на
- 38. Составляющие предлагаемого подхода Отображение данных, находящихся в “центре” и группировка данных, находящихся вне “центра”, с использованием
- 39. Построение дерева визуализации (визуализатора) При построении визуализатора на основе дерева объединений выполняются следующие шаги: Сопоставление визуализации
- 40. Обеспечение плавности перехода от одной конфигурации к другой Смещение В любой конфигурации всегда должна быть «точка
- 41. Структура хранения визуализатора Структура хранения визуализации данных – дерево (дерево визуализации), вершины которого содержат следующую информацию:
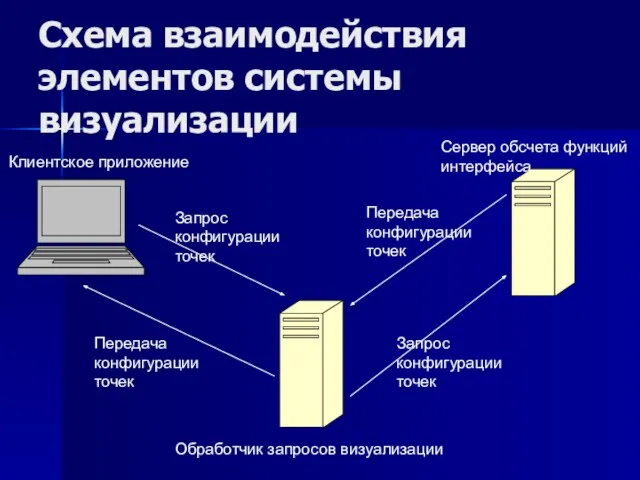
- 42. Схема взаимодействия элементов системы визуализации Запрос конфигурации точек Клиентское приложение Передача конфигурации точек Обработчик запросов визуализации
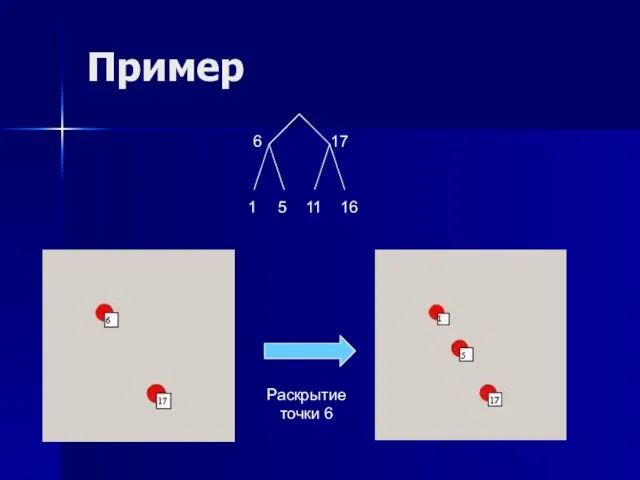
- 43. Пример 6 17 1 5 11 16 Раскрытие точки 6
- 45. Скачать презентацию































 Презентация ремонтов. Ремонт вагонов
Презентация ремонтов. Ремонт вагонов Схема жизни бетонной конструкции 3 года30-35 лет40 лет 0-3 года – набор бетоном проектной прочности 3-40 лет – незначительное уменьшение
Схема жизни бетонной конструкции 3 года30-35 лет40 лет 0-3 года – набор бетоном проектной прочности 3-40 лет – незначительное уменьшение понятливый понятой
понятливый понятой Природный газ
Природный газ Музыка и изобразительное искусство
Музыка и изобразительное искусство Старший кассир, кассир
Старший кассир, кассир Комнатные растения в интерьере 7 класс
Комнатные растения в интерьере 7 класс Тьюторская тема
Тьюторская тема Классный час
Классный час Все мы родом из детства Зам.директора ВР Пыжик Т.Е.
Все мы родом из детства Зам.директора ВР Пыжик Т.Е. Психологическое сопровождение
Психологическое сопровождение ПТК Восточной Сибири. Полуостров Таймыр
ПТК Восточной Сибири. Полуостров Таймыр ЕГЭ 2010
ЕГЭ 2010 Всемирный День студента
Всемирный День студента Девиантное поведение. 8 класс
Девиантное поведение. 8 класс Профпригодность. Тесты
Профпригодность. Тесты МАСТЕРСКАЯ-ПРАКТИКУМ ПО ЭРГОНОМИЧЕСКИМ ОСНОВАМ ПРОЕКТИРОВАНИЯ ПОЛЬЗОВАТЕЛЬСКИХ ИНТЕРФЕЙСОВ
МАСТЕРСКАЯ-ПРАКТИКУМ ПО ЭРГОНОМИЧЕСКИМ ОСНОВАМ ПРОЕКТИРОВАНИЯ ПОЛЬЗОВАТЕЛЬСКИХ ИНТЕРФЕЙСОВ «У солнышка в гостях»
«У солнышка в гостях» Схема взаимосвязей образовательных понятий
Схема взаимосвязей образовательных понятий Монеты древней руси
Монеты древней руси СССР в годы Хрущевской оттепели 1953-1964
СССР в годы Хрущевской оттепели 1953-1964 «Путь к звездам»
«Путь к звездам» Солнце – вечный огонь Вселенной. Солнечная система
Солнце – вечный огонь Вселенной. Солнечная система Java Script Examples
Java Script Examples Работа на швейной машинке
Работа на швейной машинке Питание растений 6 класс
Питание растений 6 класс Организации вебинара
Организации вебинара Подписки Билайн: масс-медиа нового поколения
Подписки Билайн: масс-медиа нового поколения