Кластеризация данных

05.10.2006
СПбГУ ИТМО
План доклада
Основные определения
Общая схема кластеризации
Популярные алгоритмы
Применения кластеризации

05.10.2006
СПбГУ ИТМО
Что такое кластеризация?
Кластеризация – это автоматическое разбиение элементов некоторого множества (объекты, данные, вектора характеристик) на группы (кластеры) по принципу схожести.

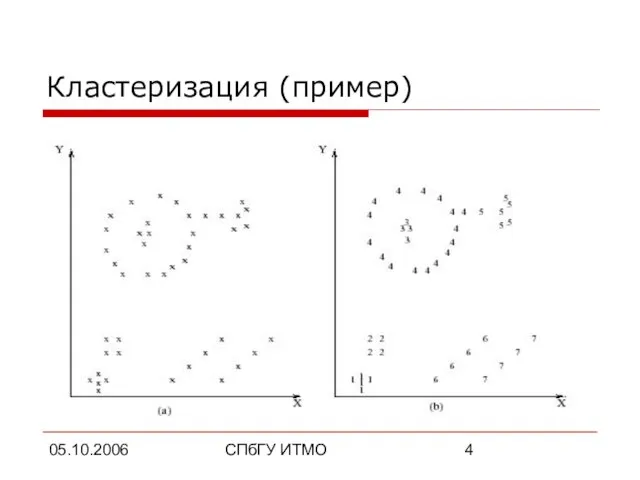
05.10.2006
СПбГУ ИТМО
Кластеризация (пример)

05.10.2006
СПбГУ ИТМО
Разница между
кластеризацией и классификацией
Кластеризация (unsupervised classification) разбивает множество объектов на группы, которые определяются только ее результатом.
Классификация (supervised classification) относит каждый объект к одной из заранее определенных групп.

05.10.2006
СПбГУ ИТМО
Зачем нужна кластеризация?
Много практических применений в информатике и других областях:
Анализ данных (Data mining);
Группировка и распознавание объектов;
Извлечение и поиск информации.
Это важная форма абстракции данных.
Это активно развивающаяся область теоретической информатики.

05.10.2006
СПбГУ ИТМО
Формальные определения
Вектор характеристик (объект) x – единица данных для алгоритма кластеризации. Обычно это элемент d-мерного пространства: x = (x1, …, xd).
Характеристика (атрибут) xi – скалярная компонента вектора x.
Размерность d – количество характеристик объекта x.

05.10.2006
СПбГУ ИТМО
Формальные определения (продолжение)
Множество объектов X = {x1, …, xn} – набор входных данных. i-й объект из X определяется как xi = (xi,1, …, xi,d). Часто X представляют в виде матрицы характеристик размера n x d.
Кластер – подмножество «близких друг к другу» объектов из X.
Расстояние d(xi, xj) между объектами xi и xj– результат применения выбранной метрики (или квази-метрики) в пространстве характеристик.

05.10.2006
СПбГУ ИТМО
Постановка задачи
Цель кластеризации – построить оптимальное разбиение объектов на группы:
разбить N объектов на k кластеров;
просто разбить N объектов на кластеры.
Оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:

05.10.2006
СПбГУ ИТМО
План доклада
Основные определения
Общая схема кластеризации
Популярные алгоритмы
Применения кластеризации

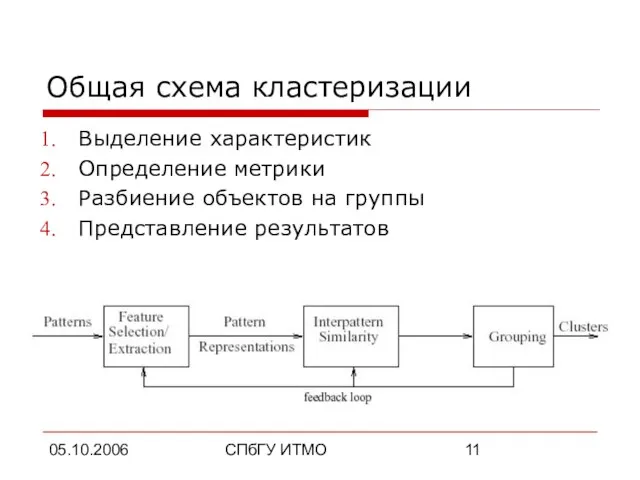
05.10.2006
СПбГУ ИТМО
Общая схема кластеризации
Выделение характеристик
Определение метрики
Разбиение объектов на группы
Представление результатов

05.10.2006
СПбГУ ИТМО
Выделение характеристик
Выбор свойств, характеризующих объекты:
количественные характеристики (координаты, интервалы…);
качественные характеристики (цвет, статус, воинское звание…).
Уменьшение размерности пространства, нормализация характеристик.
Представление объектов в виде характеристических векторов.

05.10.2006
СПбГУ ИТМО
Выбор метрики
Метрика выбирается в зависимости от:
пространства, где расположены объекты;
неявных характеристик кластеров.
Если все координаты объекта непрерывны и вещественны, а кластеры должны представлять собой нечто вроде гиперсфер, то используется классическая метрика Евклида (на самом деле, чаще всего так и есть):

05.10.2006
СПбГУ ИТМО
План доклада
Основные определения
Общая схема кластеризации
Популярные алгоритмы
Применения кластеризации

05.10.2006
СПбГУ ИТМО
Алгоритмы кластеризации
Иерархические алгоритмы
Минимальное покрывающее дерево
k-Means алгоритм (алгоритм k-средних)
Метод ближайшего соседа
Алгоритмы нечеткой кластеризации
Применение нейронных сетей
Генетические алгоритмы
Метод закалки

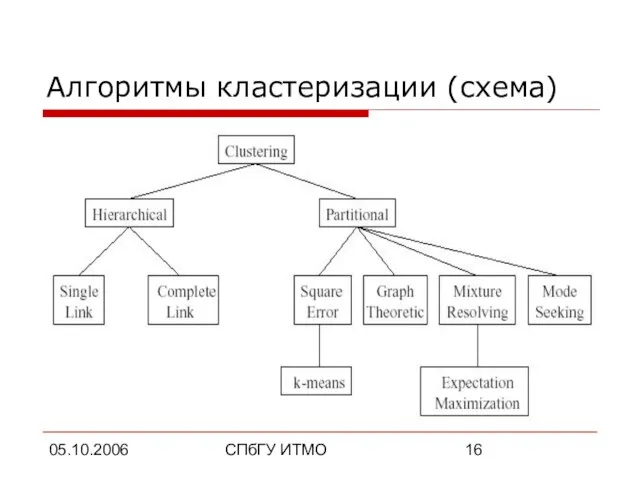
05.10.2006
СПбГУ ИТМО
Алгоритмы кластеризации (схема)

05.10.2006
СПбГУ ИТМО
Классификация алгоритмов
Строящие «снизу-вверх» и «сверху-вниз»
Монотетические и политетические
Непересекающиеся и нечеткие
Детерминированные и стохастические
Потоковые (online) и не потоковые
Зависящие и не зависящие от начального разбиения
Зависящие и не зависящие от порядка рассмотрения объектов

05.10.2006
СПбГУ ИТМО
Иерархические алгоритмы
Результатом работы является дендограмма (иерархия), позволяющая разбить исходное множество объектов на любое число кластеров.
Два наиболее популярных алгоритма, оба строят разбиение «снизу-вверх»:
Single-link – на каждом шаге объединяет два кластера с наименьшим расстоянием между двумя наиболее близкими представителями;
Complete-link – объединяет кластеры с наименьшим расстоянием между двумя наиболее удаленными представителями.

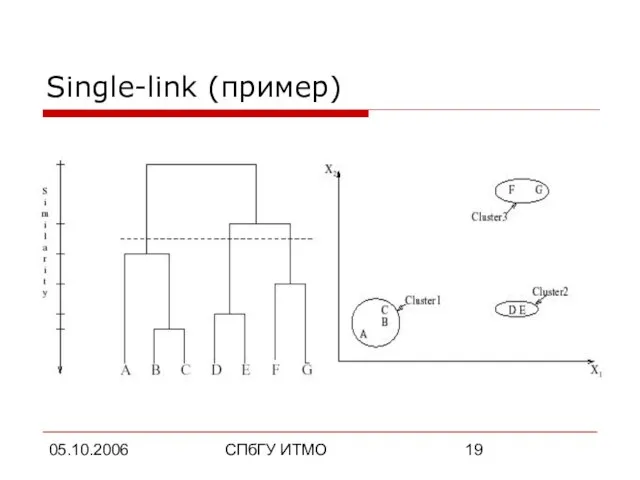
05.10.2006
СПбГУ ИТМО
Single-link (пример)

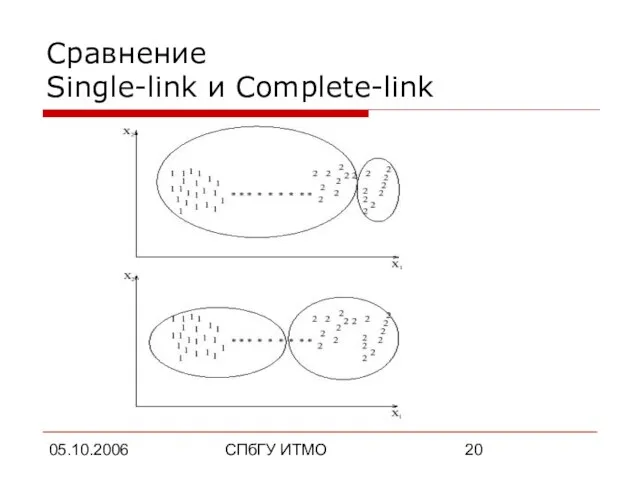
05.10.2006
СПбГУ ИТМО
Сравнение
Single-link и Complete-link

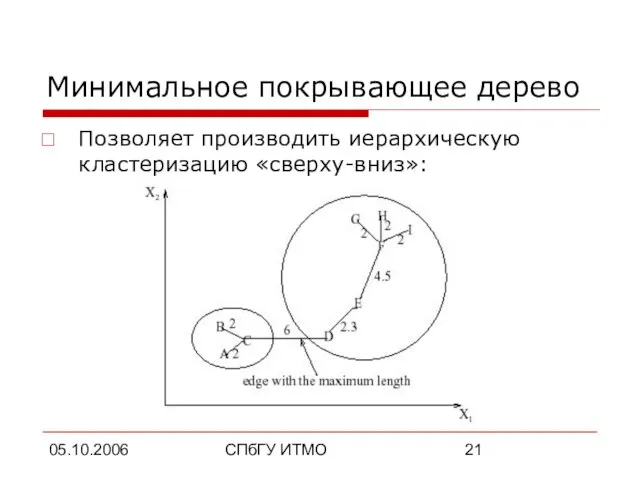
05.10.2006
СПбГУ ИТМО
Минимальное покрывающее дерево
Позволяет производить иерархическую кластеризацию «сверху-вниз»:

05.10.2006
СПбГУ ИТМО
k-Means алгоритм
Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров (любые k из n объектов, или вообще k случайных точек).
Отнести каждый объект к кластеру с ближайшим «центром масс».
Пересчитать «центры масс» кластеров согласно текущему членству.
Если критерий остановки алгоритма не удовлетворен, вернуться к шагу 2.

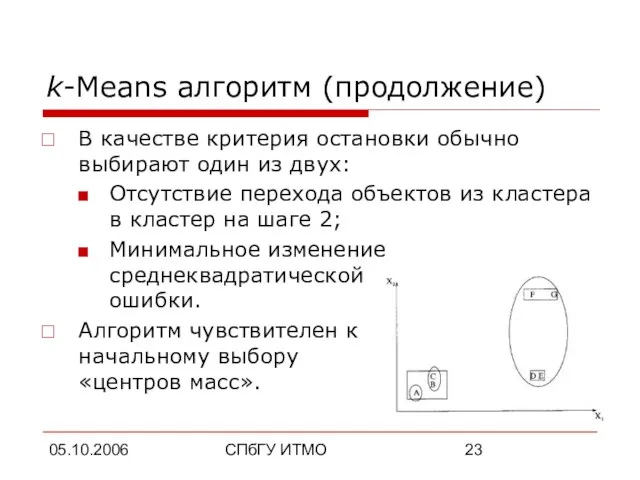
05.10.2006
СПбГУ ИТМО
k-Means алгоритм (продолжение)
В качестве критерия остановки обычно выбирают один из двух:
Отсутствие перехода объектов из кластера в кластер на шаге 2;
Минимальное изменение среднеквадратической
ошибки.
Алгоритм чувствителен к
начальному выбору
«центров масс».

05.10.2006
СПбГУ ИТМО
Метод ближайшего соседа
Один из старейших (1978), простейших и наименее оптимальных алгоритмов:
Пока существуют объекты вне кластеров {
Для каждого такого объекта выбрать ближайшего соседа, кластер которого определен, и если расстояние до этого соседа меньше порога – отнести его в тот же кластер, иначе можно создать новый;
Увеличить порог при необходимости;
}

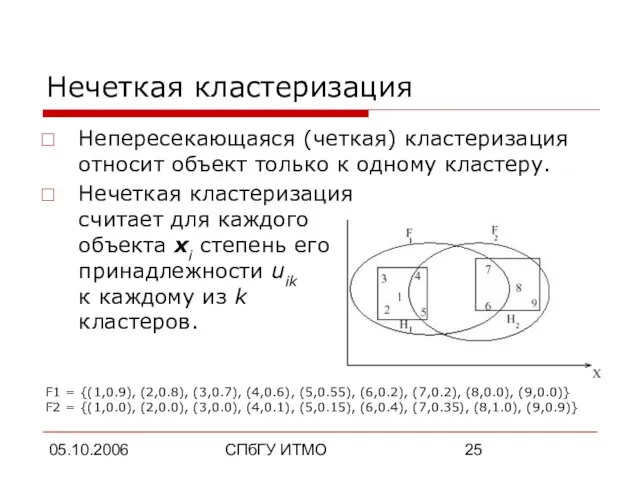
05.10.2006
СПбГУ ИТМО
Нечеткая кластеризация
Непересекающаяся (четкая) кластеризация относит объект только к одному кластеру.
Нечеткая кластеризация
считает для каждого
объекта xi степень его
принадлежности uik
к каждому из k
кластеров.
F1 = {(1,0.9), (2,0.8), (3,0.7), (4,0.6), (5,0.55), (6,0.2), (7,0.2), (8,0.0), (9,0.0)}
F2 = {(1,0.0), (2,0.0), (3,0.0), (4,0.1), (5,0.15), (6,0.4), (7,0.35), (8,1.0), (9,0.9)}

05.10.2006
СПбГУ ИТМО
Схема нечеткой кластеризации
Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k (обычно )
Используя матрицу U, найти значение критерия нечеткой ошибки (например,
).
Перегруппировать объекты с целью ее уменьшения.
Пока матрица U меняется, повторять шаг 2.

05.10.2006
СПбГУ ИТМО
Применение нейронных сетей
Искусственные нейронные сети (ИНС) легко работают в распределенных системах в силу своей природы.
ИНС могут проводить кластеризацию только для объектов с числовыми атрибутами.
Настройка весовых коэффициентов ИНС помогает сделать выбор характеристик
(этап 1 кластеризации) менее субъективным.
Кластеризация с применением самоорганизующихся карт Кохонена эквивалентна алгоритму k-Means.

05.10.2006
СПбГУ ИТМО
Генетические алгоритмы
Выбрать начальную случайную популяцию для множества решений. Получить оценку качества для каждого решения (~ 1 / e2).
Создать и оценить следующую популяцию решений, используя операторы:
выбора – предпочитает хорошие решения;
рекомбинации («кроссовер») – создает новое решение из двух существующих;
мутации – создает новое решение из случайного изменения существующего.
Повторять шаг 2 пока это необходимо.

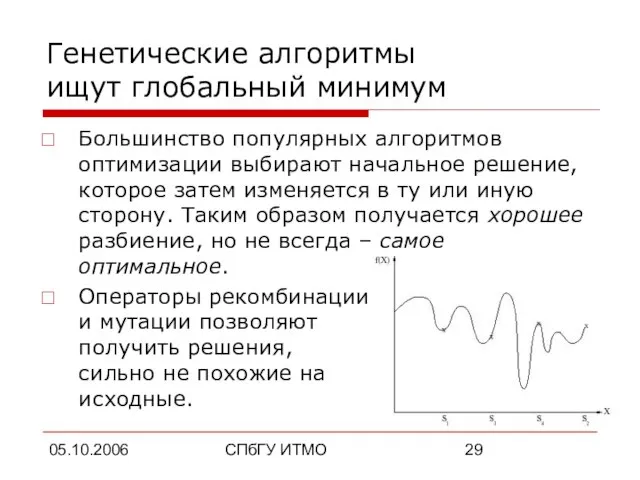
05.10.2006
СПбГУ ИТМО
Генетические алгоритмы
ищут глобальный минимум
Большинство популярных алгоритмов оптимизации выбирают начальное решение, которое затем изменяется в ту или иную сторону. Таким образом получается хорошее разбиение, но не всегда – самое оптимальное.
Операторы рекомбинации
и мутации позволяют
получить решения,
сильно не похожие на
исходные.

05.10.2006
СПбГУ ИТМО
Метод закалки
Пытается найти глобальный оптимум, однако работает только с одним текущим решением.
Случайно выбрать начальное разбиение P0 и сосчитать ошибку EP0. Выбрать значения начальной и конечной температур (T0 > Tf).
Выбрать P1 невдалеке от P0. Если EP0 > EP1, то утвердить P1, иначе – P1, но с вероятностью, зависящей от разницы температур. Повторить выбор соседних разбиений несколько раз.
Чуть-чуть «остыть»: T0 = c * T0, где c < 1. Если T0 > Tf – снова на шаг 2, иначе – стоп.

05.10.2006
СПбГУ ИТМО
Какой алгоритм выбрать?
Генетические алгоритмы и искусственные нейронные сети хорошо распараллеливаются.
Генетические алгоритмы и метод закалки осуществляют глобальный поиск, но метод закалки сходится о-о-очень медленно.
Генетические алгоритмы хорошо работают только для одно- (двух-) мерных объектов, зато не требуется непрерывность координат.

05.10.2006
СПбГУ ИТМО
Какой алгоритм выбрать? (продолжение)
k-Means быстро работает и прост в реализации, но создает только кластеры, похожие на гиперсферы.
Иерархические алгоритмы дают оптимальное разбиение на кластеры, но их трудоемкость квадратична.
На практике лучше всего зарекомендовали себя гибридные подходы, где шлифовка кластеров выполняется методом k-Means, а первоначальное разбиение – одним из более сильных методов.

05.10.2006
СПбГУ ИТМО
Априорное использование
природы кластеров в алгоритмах
Неявное использование:
выбор соответствующих характеристик объектов из всех характеристик
выбор метрики (метрика Евклида обычно дает гиперсферические кластеры)
Явное использование:
подсчет схожести (использование ∞ для расстояния между объектами из заведомо разных кластеров)
представление результатов (учет явных ограничений)

05.10.2006
СПбГУ ИТМО
Кластеризация
больших объемов данных
Обычно используют k-Means или его гибридные модификации.
Если множество объектов не помещается в основную память, можно:
проводить кластеризацию по принципу «разделяй и властвуй»;
использовать потоковые (on-line) алгоритмы (например, leader, модификация метода ближайшего соседа);
использовать параллельные вычисления.

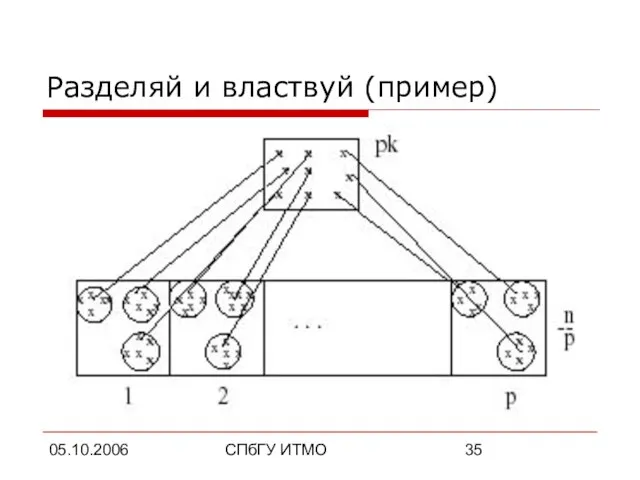
05.10.2006
СПбГУ ИТМО
Разделяй и властвуй (пример)

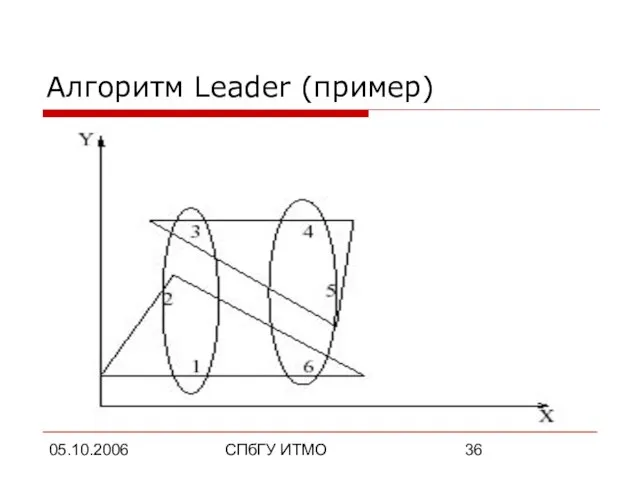
05.10.2006
СПбГУ ИТМО
Алгоритм Leader (пример)

05.10.2006
СПбГУ ИТМО
Представление результатов
Обычно используется один из следующих способов:
представление кластеров центроидами;
представление кластеров набором характерных точек;
представление кластеров их ограничениями.

05.10.2006
СПбГУ ИТМО
План доклада
Основные определения
Общая схема кластеризации
Популярные алгоритмы
Применения кластеризации

05.10.2006
СПбГУ ИТМО
Применения кластеризации
Анализ данных (Data mining)
Упрощение работы с информацией
Визуализация данных
Группировка и распознавание объектов
Распознавание образов
Группировка объектов
Извлечение и поиск информации
Построение удобных классификаторов

05.10.2006
СПбГУ ИТМО
Анализ данных (Data mining)
Упрощение работы с информацией:
достаточно работать только с k представителями кластеров;
легко найти «похожие» объекты – такой поиск применяется в ряде поисковых движков (http://www.nigma.ruлегко найти «похожие» объекты – такой поиск применяется в ряде поисковых движков (http://www.nigma.ru, http://www.vivisimo.com, …);
автоматическое построение каталогов.
Наглядное представление кластеров позволяет понять структуру множества объектов в пространстве.

05.10.2006
СПбГУ ИТМО
http://www.nigma.ru (пример)

05.10.2006
СПбГУ ИТМО
Группировка и распознавание объектов
Распознавание образов (OCR и др.):
построение кластеров на основе большого набора учебных данных;
пометка каждого из кластеров;
ассоциация каждого объекта на входе алгоритма распознавания с меткой соответствующего кластера.
Группировка объектов:
сегментация изображений;
уменьшение количества информации.

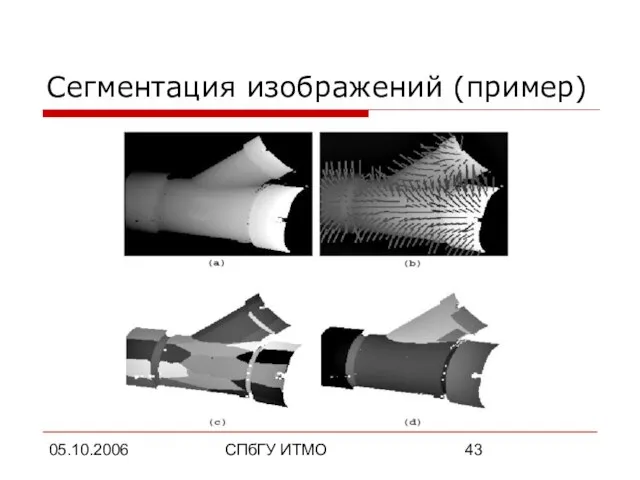
05.10.2006
СПбГУ ИТМО
Сегментация изображений (пример)

05.10.2006
СПбГУ ИТМО
Извлечение и поиск информации
(на примере книг в библиотеке)
LCC (Library of Congress Classification):
Метки с QA76 до QA76.8 – книги по CS.
Проблемы LCC:
книга относится только к одной категории;
классификация отстает от быстрого развития некоторых областей науки.
Выручает автоматическая кластеризация:
Нечеткое разбиение на группы решает проблему одной категории;
Кластеры вырастают с развитием области.

05.10.2006
СПбГУ ИТМО
Итого
Кластеризация – это автоматическое разбиение множества объектов на группы по принципу схожести
Общая схема кластеризации одна (выделение характеристик -> выбор метрики -> группировка объектов -> представление результатов). Но существует много различных реализаций этой схемы.
Кластеризация данных широко применяется в современной информатике.