Слайд 2ТЕЧЕНИЕ БЕНАРА – РЭЛЕЯ В ТОНКОМ СЛОЕ ЖИДКОСТИ ИЛИ ГАЗА
Хаотические сигналы
В 60-х
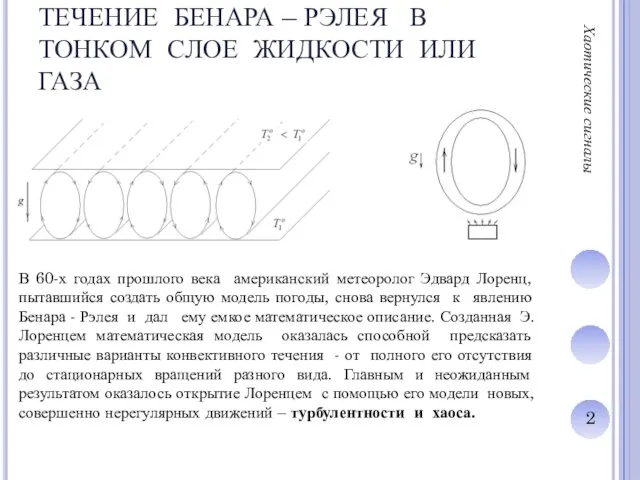
годах прошлого века американский метеоролог Эдвард Лоренц, пытавшийся создать общую модель погоды, снова вернулся к явлению Бенара - Рэлея и дал ему емкое математическое описание. Созданная Э.Лоренцем математическая модель оказалась способной предсказать различные варианты конвективного течения - от полного его отсутствия до стационарных вращений разного вида. Главным и неожиданным результатом оказалось открытие Лоренцем с помощью его модели новых, совершенно нерегулярных движений – турбулентности и хаоса.
Слайд 3ДИНАМИЧЕСКАЯ СИСТЕМА ЛОРЕНЦА
Хаотические сигналы
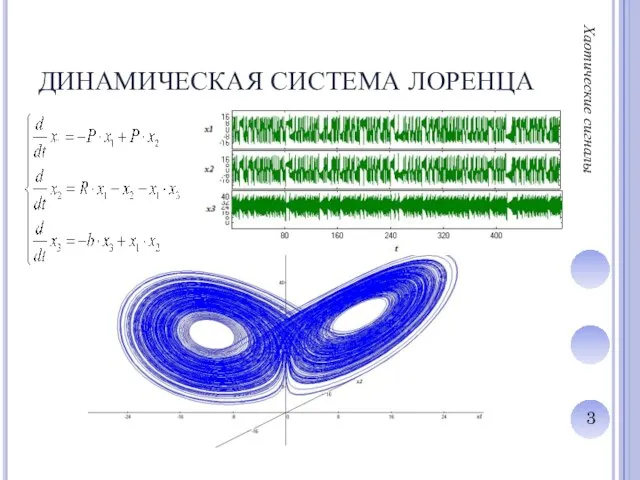
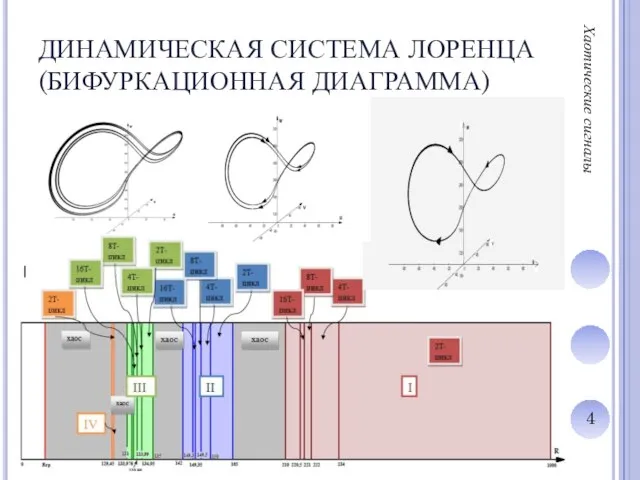
Слайд 4ДИНАМИЧЕСКАЯ СИСТЕМА ЛОРЕНЦА
(БИФУРКАЦИОННАЯ ДИАГРАММА)
Хаотические сигналы
Слайд 5ДИНАМИЧЕСКАЯ СИСТЕМА РЁССЛЕРА
Хаотические сигналы
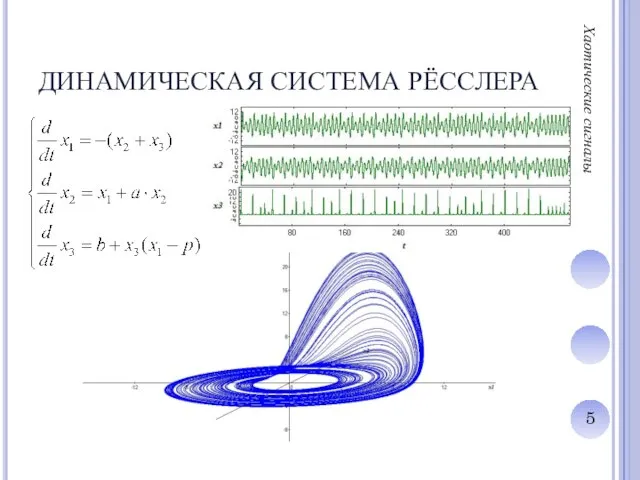
Слайд 6ДИНАМИЧЕСКАЯ СИСТЕМА РЁССЛЕРА
(КАРТА ДИНАМИЧЕСКИХ РЕЖИМОВ)
Хаотические сигналы
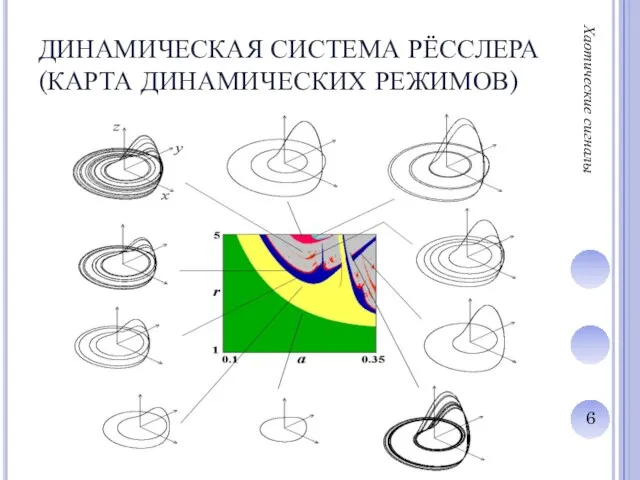
Слайд 7ОСЦИЛЛЯТОР ДУФФИНГА
Хаотические сигналы
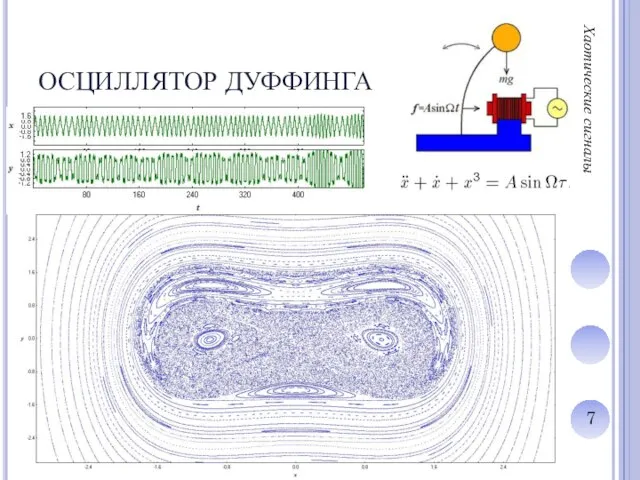
Слайд 8ОСЦИЛЛЯТОР ДУФФИНГА
(КАРТА ДИНАМИЧЕСКИХ РЕЖИМОВ)
Хаотические сигналы
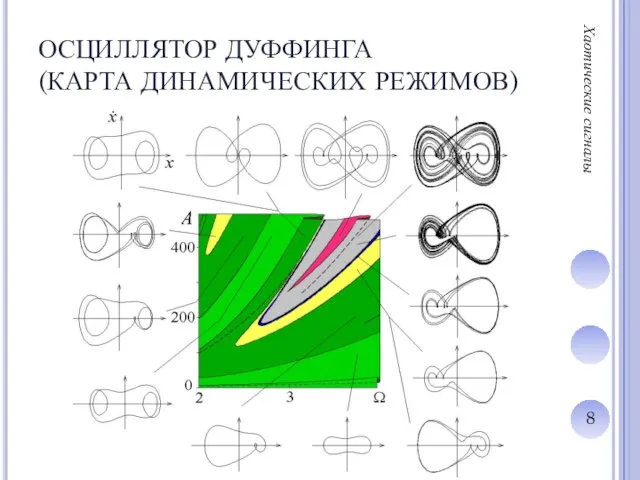
Слайд 9СХЕМА ЛЕОНА ЧУА
Хаотические сигналы
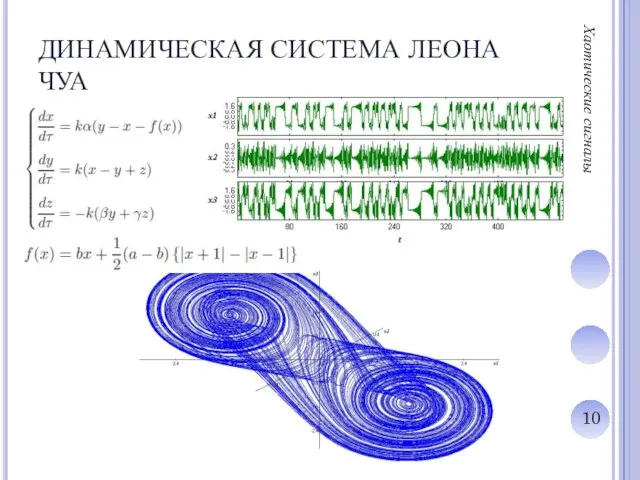
Слайд 10ДИНАМИЧЕСКАЯ СИСТЕМА ЛЕОНА ЧУА
Хаотические сигналы
Слайд 11СИГНАЛЫ С АДДИТИВНОЙ ФРАКТАЛЬНОЙ СТРУКТУРОЙ
Фрактальные сигналы
Функция Вейерштрасса
В реальных радиотехнических системах число членов
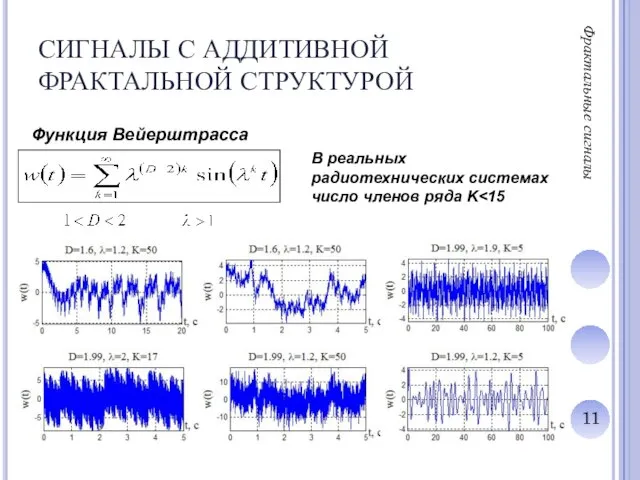
ряда K<15
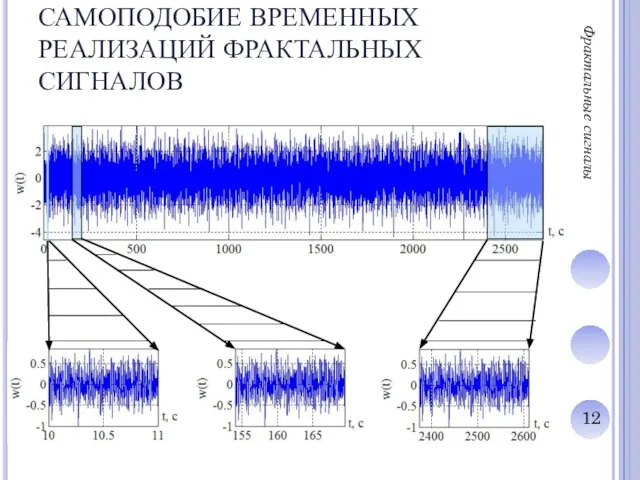
Слайд 12САМОПОДОБИЕ ВРЕМЕННЫХ РЕАЛИЗАЦИЙ ФРАКТАЛЬНЫХ СИГНАЛОВ
Фрактальные сигналы
Слайд 13СРАВНЕНИЕ РЯДОВ ВЕЙЕРШТРАССА И ФУРЬЕ
Фрактальные сигналы
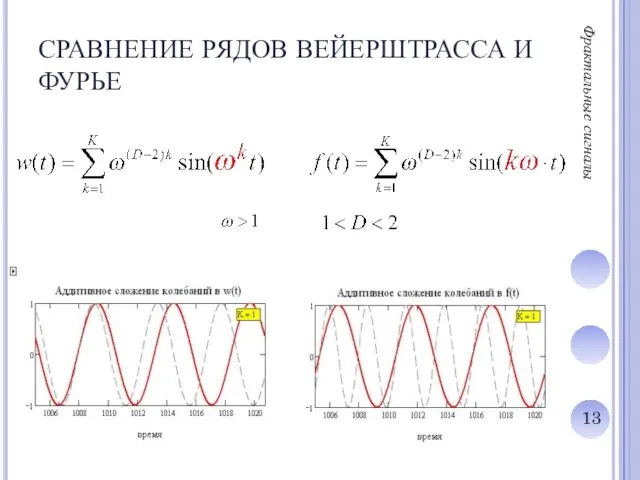
Слайд 14СРАВНЕНИЕ РЯДОВ ВЕЙЕРШТРАССА И ФУРЬЕ
Фрактальные сигналы
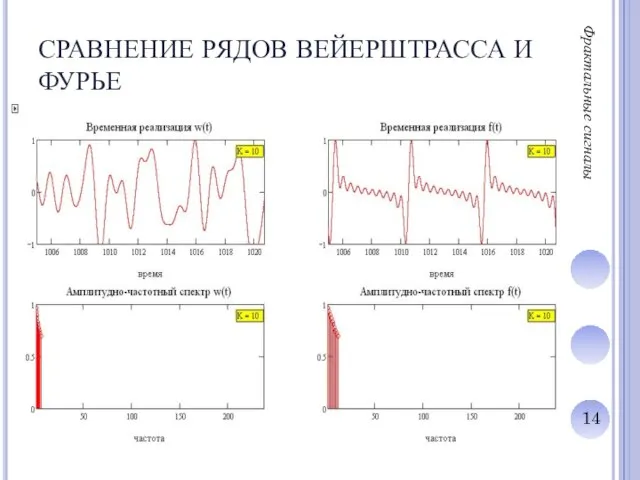
Слайд 15СИГНАЛЫ С МУЛЬТИПЛИКАТИВНОЙ ФРАКТАЛЬНОЙ СТРУКТУРОЙ
Фрактальные сигналы
САМОПОДОБИЕ В СПЕКТРАЛЬНОЙ ОБЛАСТИ
Слайд 16Фрактальные сигналы
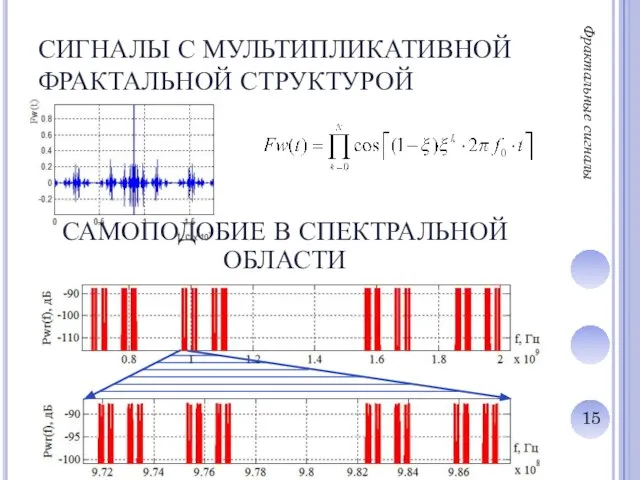
ФРАКТАЛЬНЫЕ ВЕЙВЛЕТ-СИГНАЛЫ С АДДИТИВНОЙ СТРУКТУРОЙ
СВЕРХШИРОКОПОЛОСНЫЕ ФРАКТАЛЬНЫЕ СИГНАЛЫ
Слайд 17Фрактальные сигналы
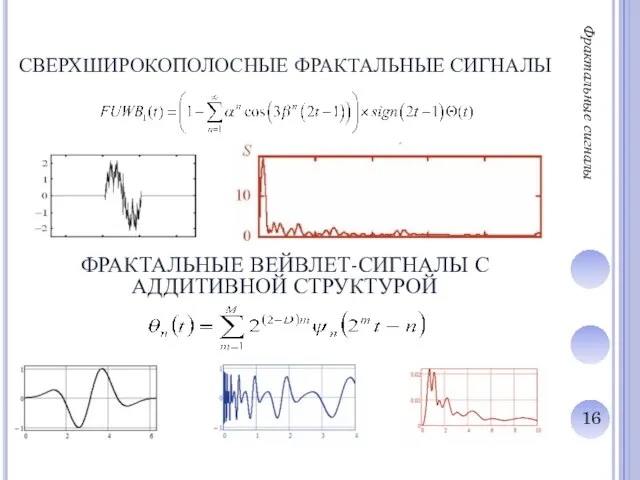
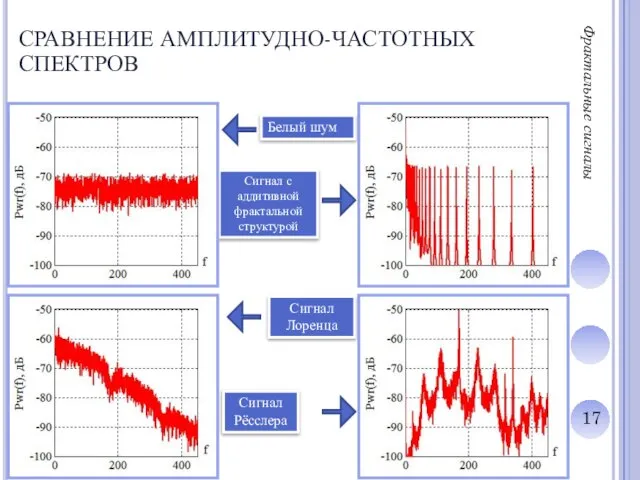
СРАВНЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ СПЕКТРОВ
Сигнал с аддитивной фрактальной структурой
Белый шум
Сигнал
Лоренца
Сигнал
Рёсслера
Слайд 18Фрактальные сигналы
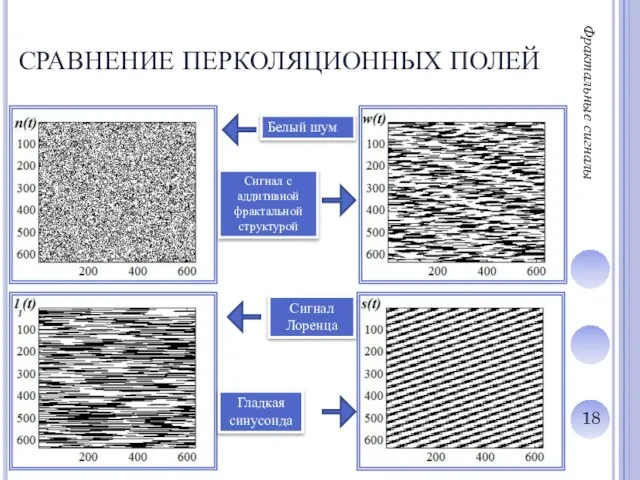
СРАВНЕНИЕ ПЕРКОЛЯЦИОННЫХ ПОЛЕЙ
Сигнал с аддитивной фрактальной структурой
Белый шум
Сигнал
Лоренца
Гладкая
синусоида

















 ЭТАПЫ РАЗРАБОТКИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
ЭТАПЫ РАЗРАБОТКИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ Презентация
Презентация Анна Ахматова
Анна Ахматова Первый тур: Первый тур: «Визитная карточка». «Визитная карточка». Проведение занятия с детьми другого образовательного учреждения
Первый тур: Первый тур: «Визитная карточка». «Визитная карточка». Проведение занятия с детьми другого образовательного учреждения Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Гражданские правоотношения. 9 класс
Гражданские правоотношения. 9 класс Дифференциальная диагностика и лечение поражений ЦНС у больных ВИЧ-инфекцией
Дифференциальная диагностика и лечение поражений ЦНС у больных ВИЧ-инфекцией Все народы воспевают мудрость старости
Все народы воспевают мудрость старости Оформление докладов и презентаций
Оформление докладов и презентаций «ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ, КАК ПУТЬ К ЖИЗНЕННОМУ УСПЕХУ»
«ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ, КАК ПУТЬ К ЖИЗНЕННОМУ УСПЕХУ» Семья
Семья Презентация на тему Эпикуреизм и Стоицизм
Презентация на тему Эпикуреизм и Стоицизм  Психология групп
Психология групп БЕЗОПАСНОСТЬ– ПРОИЗВОДИТЕЛЬНОСТЬ– ТОЧНОСТЬ:
БЕЗОПАСНОСТЬ– ПРОИЗВОДИТЕЛЬНОСТЬ– ТОЧНОСТЬ: Билет в будущее
Билет в будущее Программа начального образования
Программа начального образования Державний стандарт
Державний стандарт Прямая и косвенная речь
Прямая и косвенная речь Процессуальная реформа: как судиться по новым правилам в арбитражном суде
Процессуальная реформа: как судиться по новым правилам в арбитражном суде Как мы общаемся
Как мы общаемся Организация опционной торговли (технологическая схема)
Организация опционной торговли (технологическая схема) 20171230_geograficheskaya_igra_7_klass_vneurochka_k_shpo
20171230_geograficheskaya_igra_7_klass_vneurochka_k_shpo Презентация на тему Кишечнополостные
Презентация на тему Кишечнополостные  Конвенция по охране реки Дунай
Конвенция по охране реки Дунай Суп из рыбы Уха из консервов
Суп из рыбы Уха из консервов Десять Заповедей
Десять Заповедей Политическое лидерство
Политическое лидерство Презентация на тему Предпосылки создания Древнерусского Государства
Презентация на тему Предпосылки создания Древнерусского Государства