Содержание
- 2. Понятие конуса Рассмотрим окружность L с центром в точке О и прямую ОР, перпендикулярную к плоскости
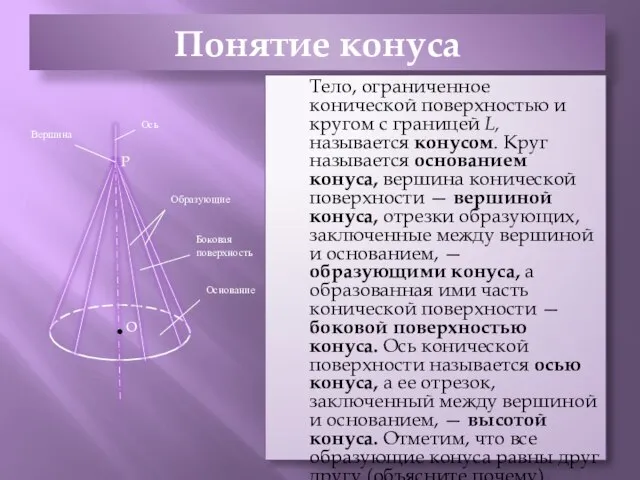
- 3. Понятие конуса Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Круг называется основанием
- 4. Конус – фигура вращения Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
- 5. Осевое сечение Рассмотрим сечение конуса различными плоскостями. Если секущая плоскость проходит через ось конуса, то сечение
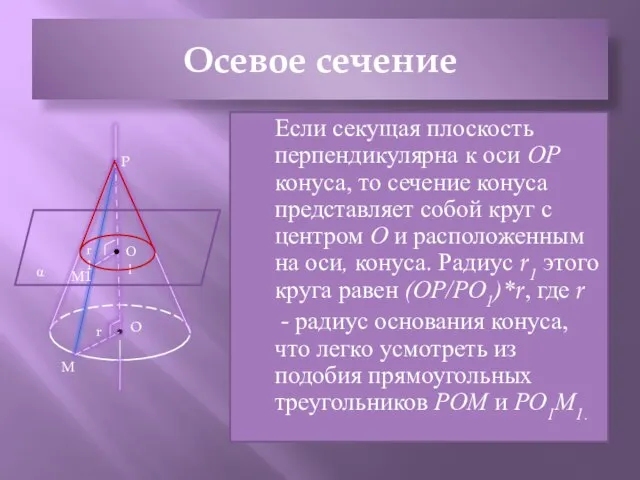
- 6. Осевое сечение Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг
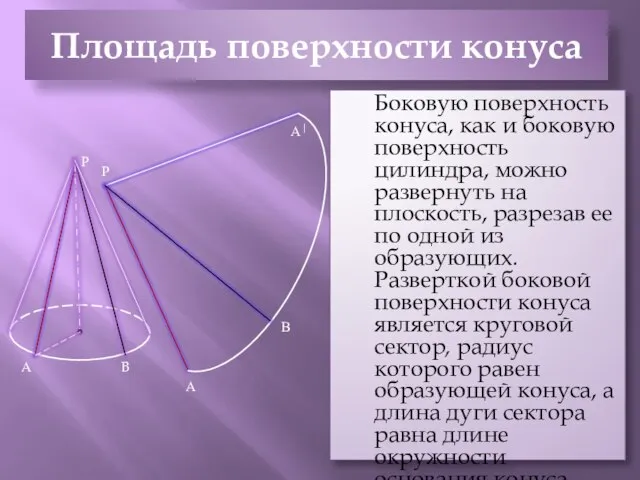
- 7. Площадь поверхности конуса Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав
- 8. Площадь поверхности конуса За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь Sбoк боковой
- 9. Площадь поверхности конуса Sбок = πl2α 360 (1)
- 10. Площадь поверхности конуса Выразим α через l и r. Так как длина дуги ABA' равна 2πr
- 11. Площадь поверхности конуса Подставив это выражение в формулу (1), получим Sбок = πrl (2)
- 12. Площадь поверхности конуса Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на
- 13. Площадь поверхности конуса Sбок = πr(l+ r)
- 14. Усеченный конус Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается
- 15. Усеченный конус Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической
- 16. Усеченный конус Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к
- 17. Усеченный конус Докажем, что площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на
- 18. Усеченный конус ▼ Пусть Р — вершина конуса, из которого получен усеченный конус, АА1 — одна
- 19. Sбок = π r * PA - π r 1 * PA = π r(PA 1
- 20. Отсюда, учитывая, что AA1 =l, находим Sбок = πrl + π(r - r1 ) PA 1
- 21. PA 1 PA = r 1 r или PA 1 + l Отсюда получаем PA 1
- 23. Скачать презентацию














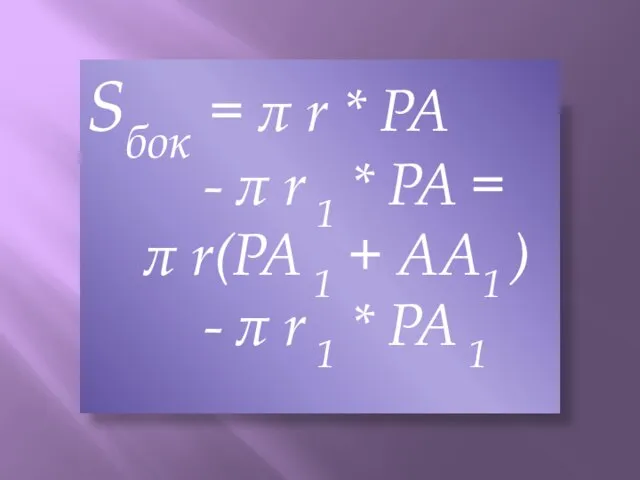


 Задержка психомоторного развития у детей до 3-х лет. Методы исследования психомоторного развития. Клинические проявления
Задержка психомоторного развития у детей до 3-х лет. Методы исследования психомоторного развития. Клинические проявления робот 15-04 (4) (1)
робот 15-04 (4) (1) "Векторный редактор CorelDraw"
"Векторный редактор CorelDraw" Буду жить под защитой Твоих
Буду жить под защитой Твоих Дисциплина на улице - залог безопасности
Дисциплина на улице - залог безопасности Если бы в моей жизни не было бы журналистики
Если бы в моей жизни не было бы журналистики Пастернак Борис Леонидович (1890-1960)
Пастернак Борис Леонидович (1890-1960) Организация работы ОВД с заявлениями и сообщениями, тема 10
Организация работы ОВД с заявлениями и сообщениями, тема 10 Организация Jeunesse Global
Организация Jeunesse Global Мультфильм. История в картинках
Мультфильм. История в картинках Приглашаем Вас в «Мир взвешенных решений»!2010 г.
Приглашаем Вас в «Мир взвешенных решений»!2010 г. The Universe
The Universe  丰 品 问 题 Product Feedback
丰 品 问 题 Product Feedback Презентация на тему История и методология юридической науки
Презентация на тему История и методология юридической науки Опыт работы Библиотеки КГТУ по списанию литературы в системе автоматизации библиотек ИРБИС
Опыт работы Библиотеки КГТУ по списанию литературы в системе автоматизации библиотек ИРБИС Information
Information Фотоконкурс Моя малая родина
Фотоконкурс Моя малая родина Урок литературногочтения
Урок литературногочтения И.М.АБРАМОВАдоцент кафедры дезинфектологииМПФ ППО 1 МГМУ им. И.М.Сеченова
И.М.АБРАМОВАдоцент кафедры дезинфектологииМПФ ППО 1 МГМУ им. И.М.Сеченова GR – менеджмент в финансовом холдинге
GR – менеджмент в финансовом холдинге Силуэты. Рисунок белки
Силуэты. Рисунок белки Великая Отечественная Война
Великая Отечественная Война  Презентация на тему Михаил Романов
Презентация на тему Михаил Романов  Статистика основного капитала
Статистика основного капитала Иллюстрации к роману Ф.М. Достоевского «Преступление и наказание»
Иллюстрации к роману Ф.М. Достоевского «Преступление и наказание» Презентация на тему Что где когда по ПДД
Презентация на тему Что где когда по ПДД но
но 1318dae32e8dd7fb
1318dae32e8dd7fb