Содержание
- 2. В п.В6 первой части ЕГЭ по математике включены задания по теме «Координатная плоскость». В презентации предложены
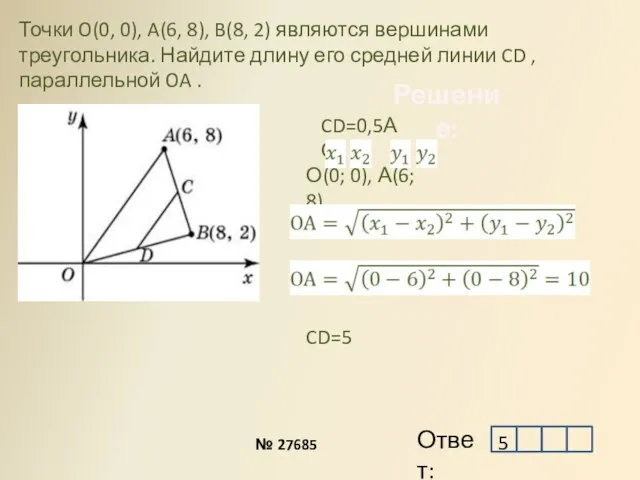
- 3. Точки O(0, 0), A(6, 8), B(8, 2) являются вершинами треугольника. Найдите длину его средней линии CD
- 4. Точки O(0, 0), A(10, 0), B(8, 6),C(2;6) являются вершинами трапеции. Найдите длину его средней линии DЕ.
- 5. Решение: Найдите абсциссу точки пересечения прямой , заданной уравнением , с осью Ox. В точке пересечения
- 6. Решение: Найдите абсциссу точки пересечения прямых, заданных уравнениями и . А(х;у) Т.к. в т.А у =
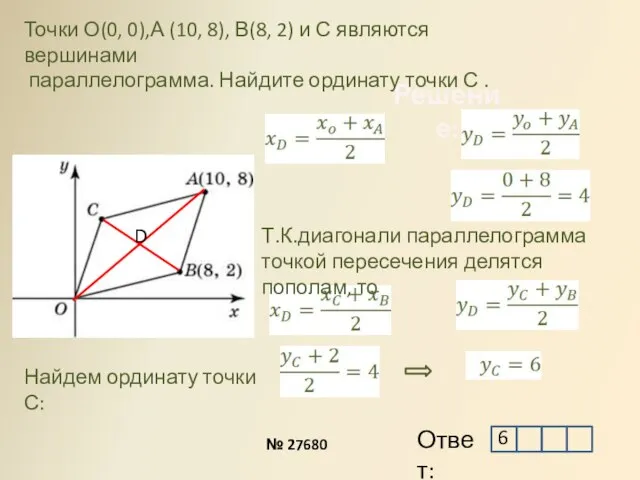
- 7. Решение: Точки О(0, 0),А (10, 8), В(8, 2) и С являются вершинами параллелограмма. Найдите ординату точки
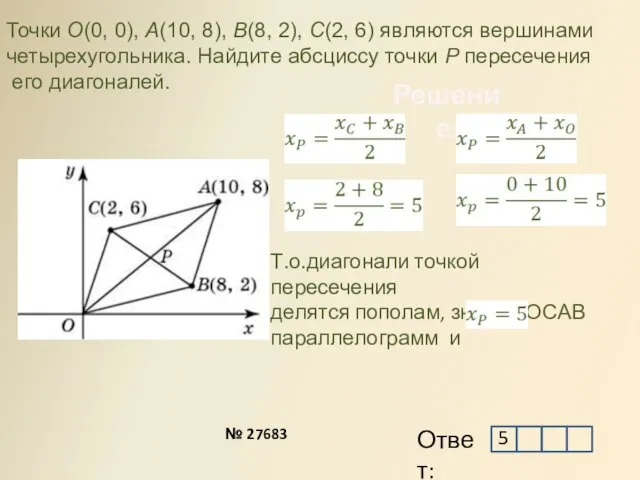
- 8. Решение: Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу точки
- 9. Решение: А(х;0) № 27670 Прямая a проходит через точки с координатами (0, 4) и (-6, 0).
- 10. Решение: С(0;у) № 27671 Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6,
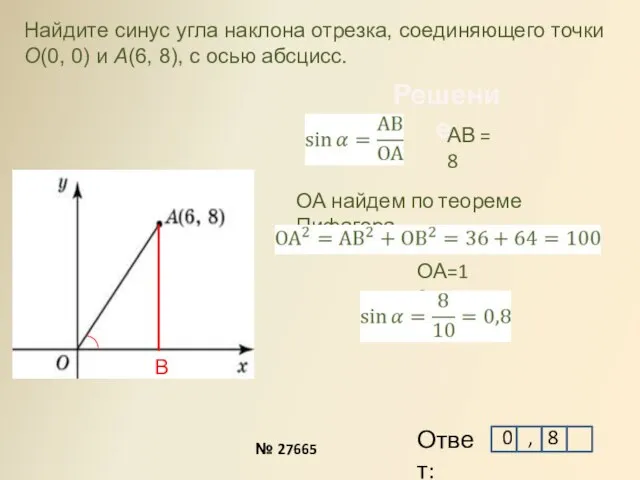
- 11. Решение: № 27665 Найдите синус угла наклона отрезка, соединяющего точки O(0, 0) и A(6, 8), с
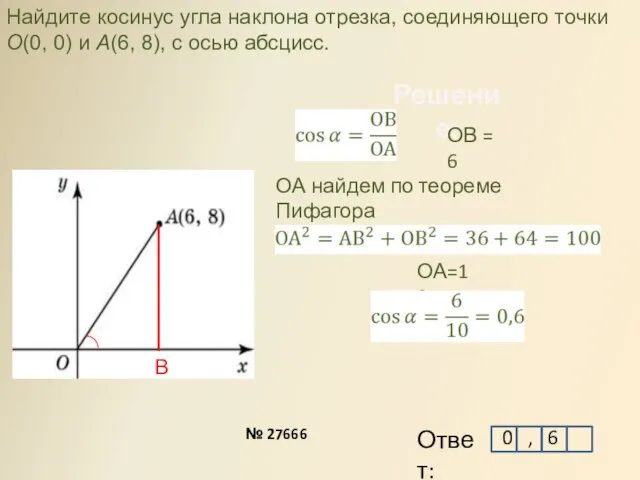
- 12. Решение: Найдите косинус угла наклона отрезка, соединяющего точки O(0, 0) и A(6, 8), с осью абсцисс.
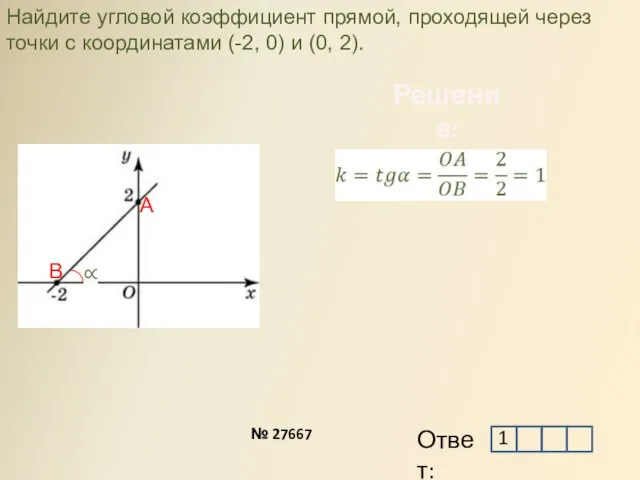
- 13. Решение: Найдите угловой коэффициент прямой, проходящей через точки с координатами (-2, 0) и (0, 2). А
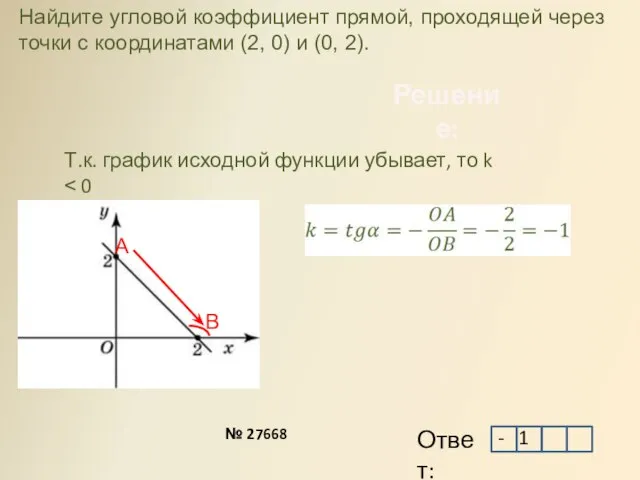
- 14. Решение: Найдите угловой коэффициент прямой, проходящей через точки с координатами (2, 0) и (0, 2). А
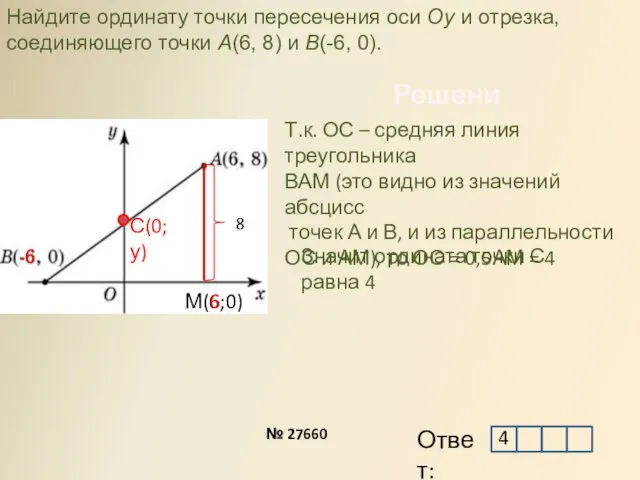
- 15. Решение: Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6, 8) и B(-6, 0).
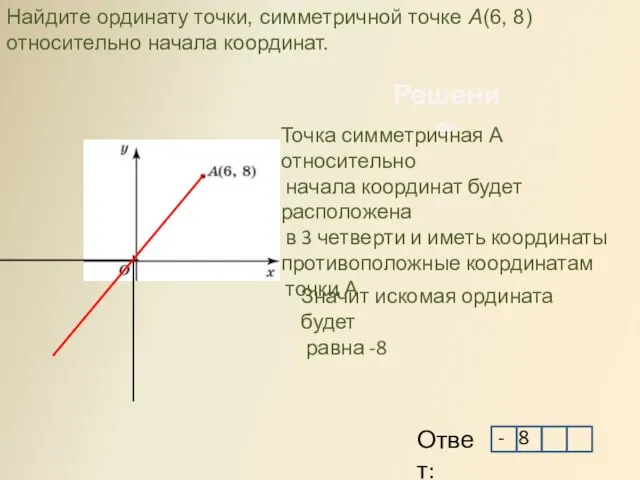
- 16. Решение: Найдите ординату точки, симметричной точке A(6, 8) относительно начала координат. Точка симметричная А относительно начала
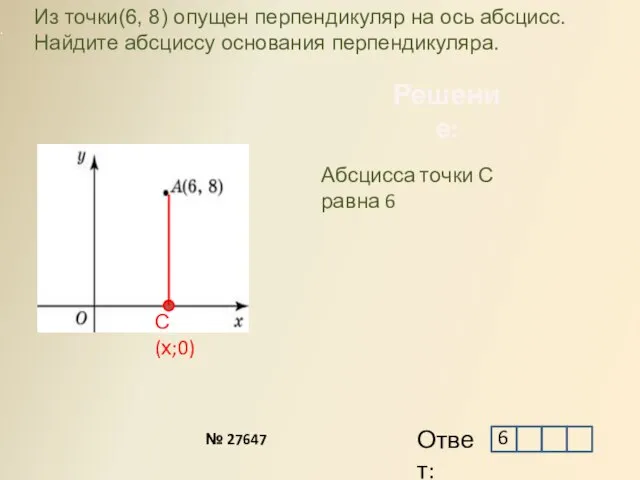
- 17. Решение: С(х;0) № 27647 Из точки(6, 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
- 19. Скачать презентацию






 Подснежник для мамы
Подснежник для мамы Внутрикорпоративный имидж и его влияние на приверженность сотрудников организации на примере ООО «Милко»
Внутрикорпоративный имидж и его влияние на приверженность сотрудников организации на примере ООО «Милко» Циклы и кризисы
Циклы и кризисы Рождество в разных странах. Традиции
Рождество в разных странах. Традиции Архетипы. Коллаж
Архетипы. Коллаж Основы фотографии и построения кадра
Основы фотографии и построения кадра Present Simple and so on
Present Simple and so on Вербальные и невербальные средства общения
Вербальные и невербальные средства общения Пирамида потребностей А. Маслоу и его вклад в развитие школы поведенческих наук
Пирамида потребностей А. Маслоу и его вклад в развитие школы поведенческих наук Презентация на тему Economic system (Экономическая система)
Презентация на тему Economic system (Экономическая система) Торнадо любви. Направление Личные Цели
Торнадо любви. Направление Личные Цели Pop art
Pop art Произведения, созданные в XIX веке, впечатлили меня сильнее литературы других времен
Произведения, созданные в XIX веке, впечатлили меня сильнее литературы других времен Правительство и конституция США
Правительство и конституция США Творчество Б.Л.Пастернака
Творчество Б.Л.Пастернака 1
1 Презентация на тему Колебательный контур, свободные и вынужденные колебания, резонанс
Презентация на тему Колебательный контур, свободные и вынужденные колебания, резонанс  Микросхемы CML для цифровой телефонии
Микросхемы CML для цифровой телефонии Слагаемые успеха в бизнесе
Слагаемые успеха в бизнесе Тренажер. Історічні дати (2 частина)
Тренажер. Історічні дати (2 частина) Эффективность освещения автомобиля
Эффективность освещения автомобиля Кинематика резания
Кинематика резания Деловые коммуникации
Деловые коммуникации Общевоинские уставы. Порядок хранения оружия и боеприпасов
Общевоинские уставы. Порядок хранения оружия и боеприпасов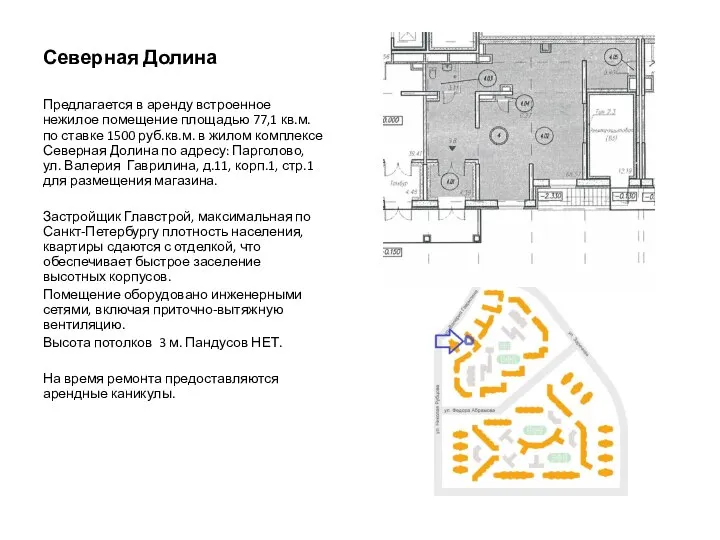 Северная Долина. Аренда встроенного нежилого помещения
Северная Долина. Аренда встроенного нежилого помещения История росписи по телу
История росписи по телу Агломерация как системный подход к развитию монопрофильных территорий
Агломерация как системный подход к развитию монопрофильных территорий Проценты в нашей жизни
Проценты в нашей жизни