Содержание
- 2. Кубик Рубика – что это такое? «Кубик Рубика» (первоначально был известен как «Магический кубик») — механическая
- 3. Эрнё Рубик Родился в Будапеште, во время Второй мировой войны. Его отец был авиаинженером на заводе
- 4. История головоломки Преподавая венгерским студентам промышленный дизайн и архитектуру, Эрнё никак не мог втолковать студентам математическую
- 5. Немного математики Число возможных различных состояний кубика Рубика равно (8! × 38−1) × (12! × 212−1)/2
- 6. Немного математики 43,252,003,274,489,856,000 возможных комбинаций Только 1 правильное решение Более 350 миллионов кубиков Рубика продано во
- 7. В 1982 году в Будапеште прошел чемпионат мира по собиранию Кубика Рубика. Для решения предлагались три
- 9. Скачать презентацию
Слайд 2Кубик Рубика – что это такое?
«Кубик Рубика» (первоначально был известен как
Кубик Рубика – что это такое?
«Кубик Рубика» (первоначально был известен как

Задача игрока заключается в том, чтобы, поворачивая грани кубика, вернуть его в такое состояние, когда каждая грань состоит из квадратов одного цвета («собрать кубик Рубика»).
Считается, что кубик Рубика — лидер среди игрушек по общему количеству продаж: по всему миру было продано порядка 350 млн кубиков Рубика, как оригинальных, так и различных аналогов.
Слайд 3Эрнё Рубик
Родился в Будапеште, во время Второй мировой войны. Его отец был авиаинженером на
Эрнё Рубик
Родился в Будапеште, во время Второй мировой войны. Его отец был авиаинженером на

В настоящее время в основном участвует в разработке видеоигр, пишет статьи по архитектуре и возглавляет студию Рубика. Награждён Государственной премией Венгрии (1983), Премией им. Дэнниса Габора (1995) и Кошутовской премией (2007).
В начале 80-х он стал редактором журнала игр и головоломок. В 1983 году основал собственную студию, которая занималась дизайном мебели и разработкой головоломок. В 1987 году получил звание профессора, а в 1990 совместно с Яношем Гинстлером основал венгерскую техническую академию и был её президентом до 1996 года.
Слайд 4История головоломки
Преподавая венгерским студентам промышленный дизайн и архитектуру, Эрнё никак не мог
История головоломки
Преподавая венгерским студентам промышленный дизайн и архитектуру, Эрнё никак не мог

Как это обычно и бывает с выдающимися изобретениями, проект кубика вынашивался не один год. Сам Рубик бился над задачей целый месяц. Но самым сложным оказалось придумать механизм.
Из центральных и рёберных кубиков с внутренней стороны вырезан фрагмент таким образом, что получается полость в виде объединения трёх цилиндров. Помимо этого, на рёберных и угловых кубиках имеются выступы особой формы. Эти выступы образуют фрагмент цилиндра, плотно входящий в полость. Благодаря такой конструкции, грани кубика свободно крутятся.
В центре конструкции вместо «невидимого кубика» находится трёхмерная крестовина, на которой свободно вращаются центральные кубики. Все остальные кубики держатся друг за друга, входя выступами в вышеуказанную выемку.
Слайд 5Немного математики
Число возможных различных состояний кубика Рубика равно (8! × 38−1) ×
Немного математики
Число возможных различных состояний кубика Рубика равно (8! × 38−1) ×

Так называемый «алгоритм Бога» для сборки Кубика Рубика не найден. С помощью больших по объёму расчётов на компьютере (7,8 ядро-лет) математик Томас Рокики (Tom Rokicki) доказал, что из любой начальной конфигурации кубик можно собрать не более чем за 23 хода, улучшив тем самым своё же прежнее достижение в 25 ходов . Для доказательства достаточности 23 ходов использовалось свободное машинное время компьютерного кластера, который использовался для создания фильмов «Человек-паук 3» и «Лови волну!».
Слайд 6Немного математики
43,252,003,274,489,856,000 возможных комбинаций
Только 1 правильное решение
Более 350 миллионов кубиков Рубика продано
Немного математики
43,252,003,274,489,856,000 возможных комбинаций
Только 1 правильное решение
Более 350 миллионов кубиков Рубика продано

На пике популярности в 1980г, головоломку крутил каждый пятый житель земли!
Размер стороны кубика Рубика - 57мм
Почти 40000 видео-роликов о головоломке на YouTube
Первый Чемпионат Мира по кубику Рубика пошел в Венгрии в 1982г и был выигран студентом из Лос-Анджелеса по имени Мин Тай (Minh Thai), собравшим кубик Рубика за 22,95сек.
Действующий чемпион мира по кубику Рубика - голландец Эрик Аккерсдик (Eric Akkersdijk), собравший головоломку за 7,08сек
Соревнования проходят в нескольких номинациях: сборка одной рукой, ногами, с закрытыми глазами и даже под водой на одном дыхании.
Считается, что дольше всех собирал свой кубик Рубика британец Грэм Паркер, получивший его в подарок на свое 19-летие и наконец собравший его впервые совсем недавно, в 47-летнем возрасте, т.е. через 26 лет!
Слайд 7
В 1982 году в Будапеште прошел чемпионат мира по собиранию Кубика Рубика.
В 1982 году в Будапеште прошел чемпионат мира по собиранию Кубика Рубика.

Для решения предлагались три задания. Засчитывалось лучшее время из трёх попыток. Все кубики были одинаково сложно запутаны 25-30 вращениями с помощью ЭВМ. От участников соревнования требовалось собрать кубик не более чем за 60 секунд. Лучшее время сборки - 22,95 секунды - показал 16-летний студент из Лос-Анджелеса Минх Тай (Minh Thai).
Рекорды и чемпионаты
Люди, увлекающиеся скоростной сборкой кубика Рубика, называются спидкуберами. А сама скоростная сборка — спидкубинг (от англ. speedcubing)
Последний мировой чемпионат (октябрь 2007 года) вновь был проведен в Будапеште.
 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось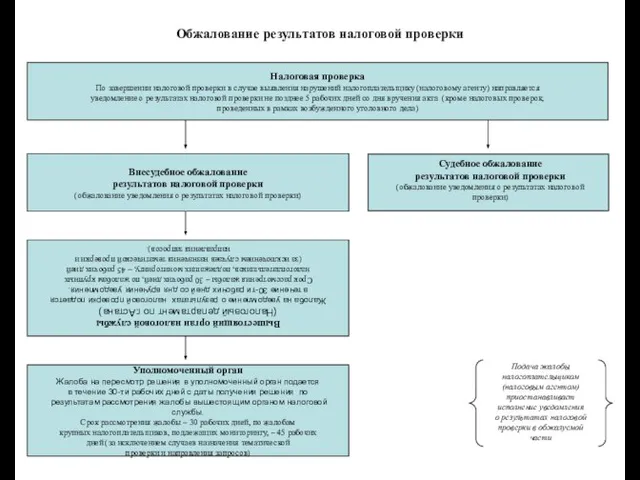 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки