Курс «Подготовка к ЕГЭ по физике» УРОК 1 ПреподавательСултанов А.Э.учитель физики ФЗФТШ при МФТИ

Начальная скорость снаряда, выпущенного вертикально вверх равна 500 м/с. В точке максимального подъёма снаряд разорвался на два осколка. Первый упал вблизи точки выстрела, имея скорость в два раза больше начальной скорости снаряда, второй упал в том же месте спустя 100 секунд после взрыва. Чему равно отношение массы первого осколка к массе второго осколка? Сопротивлением воздуха пренебречь.

Данная задача уже не первый год включается в ЕГЭ, так как очень немногие выпускники способны с ней справиться. Задача требует очень глубокого осмысления и умения правильно рассуждать.
Мы будем выполнять задачу по действиям , с максимальными пояснениями, итак:
1. Согласно условию снаряд разорвался в верхней точке, это значит, что снаряд в момент перед взрывом хоть на мгновение остановился, а это в свою очередь значит , что перед взрывом импульс снаряда равнялся нулю, mv=0.

2. После взрыва осколки полетели в разные стороны – один вверх, другой – вниз. Это первая ловушка данной задачи, о которой нужно догадаться. Осколки не могут лететь в одну сторону – оба вверх, или оба вниз, иначе нарушится закон сохранения импульса
0 = m1v1 – m2v2
Импульсы должны иметь только противоположные знаки, а это значит что снаряды движутся противоположно. Здесь m1, m2 – массы осколков, V1 , V2 - их скорости.

На основании проведённых рассуждений мы можем записать
что, m1v1 = m2v2, следовательно, m1 / m2= v2/ v1
Итак, чтобы найти соотношение масс осколков, мы должны найти соотношение их скоростей сразу после разрыва снаряда, а для этого, естественно, нужно найти сами скорости осколков.
2. Сначала найдём высоту на которую поднялся снаряд , для этого используем закон сохранения энергии :
mgh = mv02/2,
отсюда высота разрыва h= v02/2g = 12500м,
здесь v0 - начальная скорость снаряда -500 м/с.

3.Теперьнайдем начальную скорость осколка, который упал сразу вниз. Здесь очень важно правильно разобраться какими видами энергии обладал этот осколок. В момент разрыва он находился на высоте 12500 метров, значит, он обладал потенциальной энергией m1gh, кроме этого сила взрыва придала ему кинетическую энергию m1v12/2, следовательно в начале движения мы имеем
(m1v12/2 + m1gh),
в конце движения, перед ударом о землю, он обладал только кинетической энергией (m1(2v0) 2/2), энергия имеет именно такую величину, так как он перед ударом о землю имел скорость в два раза большую, чем начальная скорость снаряда.

По закону сохранения энергии можем записать:
m1v12/2 + m1gh = m1(2v0) 2/2 ,
сократим массы, получим
v12/2 + gh = (2v0) 2/2, отсюда
v1= √(4v02 - 2gh), учтём, из первого действия, что
2gh = v02 , следовательно
v1= √(4v02 - v02) = √ 3 √ v02 = √ 3 v0 = 866,7 м/с

3. Теперь найдём скорость второго осколка в момент разрыва. Главная сложность задачи именно в этом действии, дело в том, что для нахождения этой скорости нужна формула, которой пользуются очень редко – это уравнение координаты.
Общий вид уравнения координаты по оси OY имеет вид
y = y0 + v0t + at2/2,
теперь применим это уравнение к нашему случаю:
начальная координата второго осколка равна высоте, на которой разорвался снаряд: y0 = h,

начальная скорость v0 = v2 - скорости второго осколка в момент разрыва, которую нам и нужно найти,
в момент разрыва осколок двигался вверх, следовательно во второй части формулы нужно поставить знак «минус», так как движение вверх равнозамедленное,
и, наконец, ускорение a = g так как после взрыва снаряд движется в поле силы тяжести
Окончательно формула имеет вид
у = h + v2t – gt2/2

А теперь самая главная ловушка этой задачи: в конце полёта снаряд упал на землю, это значит, что в конце полёта у = 0, следовательно
0 = h + v2t – gt2/2
Выразим из этой формулы v2 :
v2= (gt2 -2h)/2t = 375 м/с
4. Теперь, наконец, можем найти то что нам необходимо, из первого действия
m1 / m2= v2/ v1 ,
Следовательно
m1 / m2 = 375/866,7 =0,43
ЗАДАЧА РЕШЕНА!!!

Средняя плотность планеты Плюк равна средней плотности Земли, а первая космическая скорость для Плюка в два раза больше, чем для Земли. Чему равно отношение периода обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, к периоду обращения аналогичного спутника Земли? Объём шара пропорционален кубу радиуса.

Данная задача также уже не первый год включается в ЕГЭ и также как и предыдущая требует очень подробного анализа.
1.Период вращения любого тела по окружности находится по формуле:
Т = 2πR/v
Чтобы найти соотношение периодов вращения спутников нужно знать соотношение скоростей- это нам дано по условию, и соотношение радиусов планет, которое нам необходимо найти

2.Сначала вспомним, как определяется первая космическая скорость:
Согласно Закону Всемирного Тяготения сила, с которой Земля притягивает спутник, находится по формуле:
F = G mпланетыmтела/ R2,
Согласно второму закону Ньютона эта же самая сила может быть найдена по другой формуле:
F =mтела а,
так как спутник вращается по круговой орбите
а- центростремительное ускорение,

а- центростремительное ускорение,
a=v2/R, следовательно
F =mтела v2/R
F = F, правые части формул равны, следовательно, левые части тоже равны:
G mпланетыmтела/ R2 = mтела v2/R
Массы тел сократим и получим выражение для первой космической скорости:
v = √ (G mпланеты/R)

2. Согласно условию задачи vплюка = 2vземли, следовательно
√ (G mплюка/Rплюка) = 2 √ (G mземли/Rземли),
Возведём обе части в квадрат и сократим G, получим
mплюка/Rплюка =4 mземли/Rземли (*)
3.Вспомним, что масса тела находится по формуле
m = ρV, где ρ- плотность тела, а V- его объём,
объём шара находится по формуле V = 4/3 π R3 следовательно масса тела
m = ρ 4/3 π R3

для планеты Плюк
mплюка = ρплюка 4/3 π R3плюка ,
для Земли
mземли = ρ земли 4/3 π R3земли
4. Вернёмся к формуле (*) из второго действия и подставим вместо масс их значения, постараемся не запутаться:
ρплюка 4/3 π R3плюка/ Rплюка =4 ρ земли 4/3 π R3земли/ Rземли
проведём сокращения с двух сторон, учитывая, что по условию плотности планет равны, получим :
R2плюка = 4 R2земли , следовательно
R плюка = 2 R земли

5. Теперь можно ответить на вопрос задачи
Период обращения спутника вокруг Плюка
Тплюка = 2πRплюка/vплюка
Период обращения спутника вокруг Земли
Тземли = 2πRземли /vземли
Тплюка / Тземли = Rплюка vземли / Rземли vплюка =
2 Rземли vземли /Rземли 2 vземли = 1
Тплюка / Тземли = 1, задача решена!!!

Горизонтально летящий снаряд разрывается на два осколка. Первый осколок летит под углом 90 градусов к первоначальному направлению полёта снаряда, а второй под углом 30 градусов к первоначальному направлению. Скорость первого осколка 10 м/с, а второго 80 м/с. Найдите отношение массы первого к массе второго осколка.

Данную задачу мы не будем разбирать так подробно как предыдущие, приведём только основное решение:
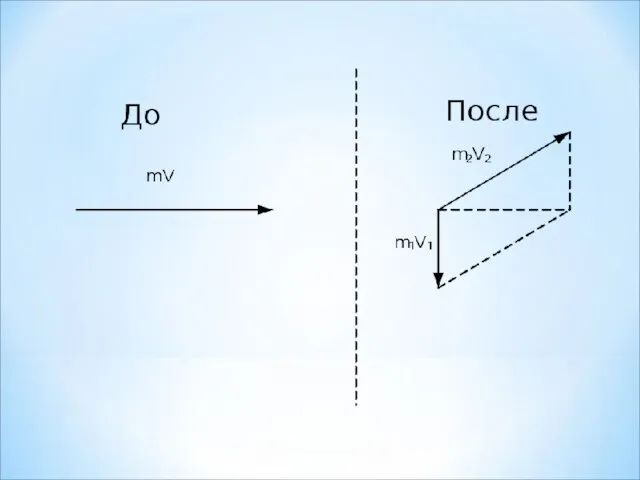
Прежде всего нужно сделать чертёж, обратите внимание, что согласно условию задачи осколки могут лететь только в разные стороны, иначе закон сохранения импульса не будет выполняться.
Запишем проекции импульсов на оси координат :

Ось ОХ :
mv = m2v2 cos α ,
Здесь α = 30°
mv – проекция импульса снаряда на
ось ОХ,
m2v2 cos α - проекция импульса второго осколка на ось ОХ
проекция импульса первого осколка m1v1 на ось ОХ равна нулю, так как вектор импульса перпендикулярен оси ОХ

Ось ОY : 0 = m2v2 sin α - m1v1
(- m1v1)- проекция импульса первого осколка на
ось ОY
m2v2 sin α - проекция импульса второго осколка
на ось ОY
Проекция импульса снаряда до взрыва на ось ОY равна нулю, так как вектор импульса перпендикулярен оси ОY

Нам нужно найти соотношение масс осколков, поэтому мы используем только второе уравнение. Заранее не известно проекция на какую ось нам понадобится, поэтому при любом решении записывают проекции на обе оси.