Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы

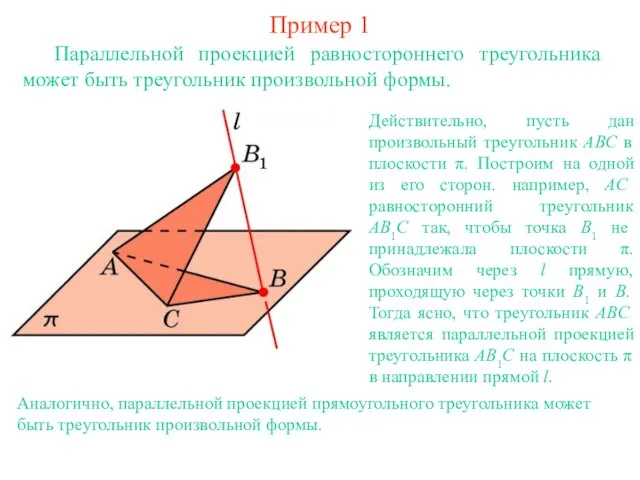
Пример 1
Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы.
Действительно, пусть дан произвольный треугольник ABC в плоскости π. Построим на одной из его сторон. например, AC равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость π в направлении прямой l.
Аналогично, параллельной проекцией прямоугольного треугольника может быть треугольник произвольной формы.

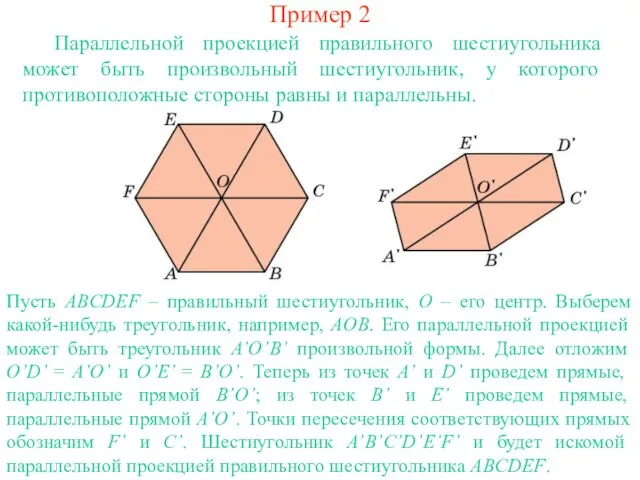
Пример 2
Параллельной проекцией правильного шестиугольника может быть произвольный шестиугольник, у которого противоположные стороны равны и параллельны.
Пусть ABCDEF – правильный шестиугольник, O – его центр. Выберем какой-нибудь треугольник, например, AOB. Его параллельной проекцией может быть треугольник A’O’B’ произвольной формы. Далее отложим O’D’ = A’O’ и O’E’ = B’O’. Теперь из точек A’ и D’ проведем прямые, параллельные прямой B’O’; из точек B’ и E’ проведем прямые, параллельные прямой A’O’. Точки пересечения соответствующих прямых обозначим F’ и C’. Шестиугольник A’B’C’D’E’F’ и будет искомой параллельной проекцией правильного шестиугольника ABCDEF.

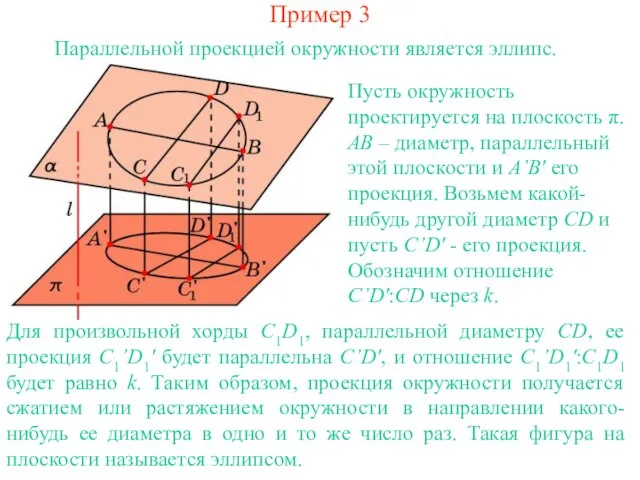
Пример 3
Параллельной проекцией окружности является эллипс.
Для произвольной хорды C1D1, параллельной диаметру CD, ее проекция C1’D1' будет параллельна C’D', и отношение C1’D1':C1D1 будет равно k. Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в одно и то же число раз. Такая фигура на плоскости называется эллипсом.
Пусть окружность проектируется на плоскость π. AB – диаметр, параллельный этой плоскости и A’B' его проекция. Возьмем какой-нибудь другой диаметр CD и пусть C’D' - его проекция. Обозначим отношение C’D':CD через k.

Упражнение 1
Какие фигуры могут служить параллельными проекциями треугольника?
Ответ: Треугольник или отрезок.

Упражнение 2
Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник?
Ответ: а), б), в) Да.

Упражнение 3
Какой фигурой может быть параллельная проекция прямоугольника?
Ответ: Параллелограммом или отрезком.

Упражнение 4
Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция?
Ответ: а), б), в) Да; г) нет.

Упражнение 5
Верно ли, что проекцией ромба, если он не проектируется в отрезок, будет ромб?
Ответ: Нет.

Упражнение 6
Параллельной проекцией каких фигур может быть квадрат?
Ответ: Параллелограммов.

Упражнение 7
В какую фигуру может проектироваться трапеция?
Ответ: Трапецию или отрезок.

Упражнение 8
Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы?
Ответ: а) Да; б), в) нет.