Квадрат суммы и квадрат разности

По какому признаку можно провести классификацию данных выражений на 2 группы?
I )(7-b)(7+b) II) (x+y)(x+y)
III) (4-a)(4-a) IV ) (c-6)(c-6)
V) (m-x)(m-x)
VI)16-x2
VII) (c+z)(c+z)
VIII) (k-t)(k+t)
IX) (5+a)(5+a) X ) 4m2-25

(7-b)(7+b)
(k-t)(k+t)
4m2-25
16-x2
(4-a)(4-a) (5+a)(5+a)
(3x+y)(3x+y)
(c-6)(c-6) (k-t)(k-t)
(c+z)(c+z)
Вспомните формулу разности квадратов
Можно применить формулу разности
квадратов
Нельзя применить формулу разности
квадратов
Устный счет

Формула разности квадратов
(a-b)(a+b)=a2-b2
или
a2-b2= (a-b)(a+b)
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы
Устный счет
Нова я
тема

Выполни умножение ,применяя формулу разности квадратов
(c+9)(c-9) 9) (2-3d3) (2+3d3)
(7-b)(7+b) 10) ( 12z2-7a4)(12z2-7a4)
(3+2x)(2x-3)
(4y2-1)(4y2-1)
(10a3+3)(10a3-3)
(1-3k)(1+3k)
(8b+5)(8b-5)
(11c+7m)(7m-11c)

Проверь себя
C2-81
49-b2
4x2-9
16y4-1
100a6-9
1-9k2
64b2-25
49c2-121m2
4-9d6
144z4-49a8
Оцени себя
«0» ошибок –
«1-2» ошибок –
«3-4» ошибок –
больше 5 ошибок -

(7-b)(7+b)
(k-t)(k+t)
4m2-25
16-x2
(4-a)(4-a) (5+a)(5+a)
(3x+y)(3x+y)
(c-6)(c-6) (k-t)(k-t)
(c+z)(c+z)
Можно применить формулу разности квадратов
Нельзя применить формулу разности
квадратов
На какие две группы можно разделить данные выражения?
Рассмотрим выражения второй группы

(c-6)(c-6)
(k-t)(k-t)
(4-a)(4-a)
(a+5)(a+5)
(3x+y)(3x+y)
(c+z)(c+z)
Можно ли в этих выражениях выполнить умножение быстрым способом?
Существует ли формула ?
На эти вопросы мы попробуем сегодня ответить в конце урока?

Проблема:
«Существует ли формула?
Если да, то какая?»

(a+5)2=
(3x+y)2=
(c+z)2=
Как можно записать эти же выражения по-другому (более компактно)?
Возведем сумму в квадрат, перемножая скобку на скобку старым способом.
= a2+5a+5a+25=
= 9x2+3xy+3xy+y2=
= c2+cz+cz+z2=
a2+10a+25
9x2+6xy+y2
c2+2cz+z2
(a+5)(a+5)
(3x+y)(3x+y)
(c+z)(c+z)
2×5a
2×3xy
2×cz

Правило умножения
многочлена нa многочлен
(a+b)(x+y)=ax+ay+bx+by

Формула квадрата
суммы
( a + b ) 2 = a 2 + 2 a b + b 2
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

Проблема:
«Существует ли формула? Если да, то какая?
Формула квадрата суммы
(a+b)2=a2+2ab+b2
Как быстро выполнить умножение второй группы выражений?
Можно ли использовать формулу квадрата суммы?
(с-6)(с-6)
(4-a)(4-a)
(k-t)(k-t)

(с-6)2=
(k-t)2=
(4-a)2=
Как можно записать эти же выражения по-другому (более компактно)?
Возведем разность в квадрат, перемножая скобку на скобку старым способом.
= c2-6c-6c+36=
= k2-kt-kt+t2=
= 16-4a-4a+a2=
C2-12c+36
K2-2kt+t2
16-8a+a2
(c-6)(c-6)
(k-t)(k-t)
(4-a)(4-a)
2×6c
2×kt
2×4a

Формула квадрата разности
(a-b)2=a2-2ab+b2
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.

Проблема:
«Существует ли формула? Если да, то какая?
Формула квадрата суммы формула квадрата разности
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2

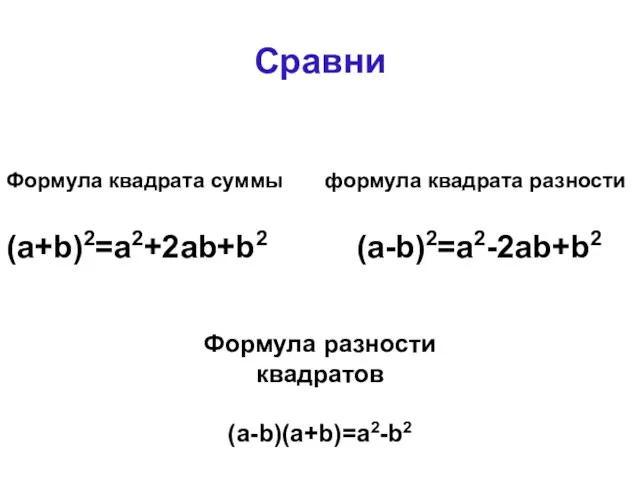
Сравни
Формула квадрата суммы формула квадрата разности
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
Формула разности квадратов
(a-b)(a+b)=a2-b2

упражнения
Уровень сложности

Выполни умножение ,применяя формулы:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
(3a+1)2
(8a-3)2
(a+2b)2
(1+3a)2
(4a-3)2
( c-4 )2
( m +d )2
(5a-6b)2
(4t+3a)2
(a-1)2
(4z-8n)2
(3a+2d)2
(3s-8n)2
(1-4f)2
(6-5c)2
(1-3ab)2
(5xy+1)2
(3ab-3t)2
(xy-4m)2
(2cd-7z)2
(1+5xyz)2
(2a+3bc)2
(4a-3kn)2
(3a-4t)2
(4a-7c)2
(9x+5z)2
(1-3a)2
(4xy+1)2
(5s+2p)2
(1-9a)2
4a2 +4ab+b2
4a2- 4ab+b2
9a2 - 60ab+100b2
4x2 -20xb+25b2
1- 6b+9b2
16a2 +8a+1
b2 -2a b +a2
a2b 2 +2ab+1
1- 16c +64c2
1+10a +25a2

(3a4 +2b 8 )2
(4x2 -3z 4 )2
(1- 5x2 y 4 z6 )2
(2a 4 +3k2 )2
(9a -2d 2 )2
(4a4 b +1)2
(2m2 n -3)4
(6a 2 b +c 2 )4
(2x 2 +5y6 z3 )4
(a 3 b5 – c2 d )3
25 x2 -30x +9
81b2 -36b +4
9 y 2+24y +16
49 z2 – 28mz+4m2
100a2 +80az +16z2
1 – 6d +9 d2
121p4 + 44p 2t+4t2
169 – 78a2 +9a4
4b9 -12b3 c2 +9c4
1+ 20ab2 +100a2b4
Выполни умножение ,применяя формулы:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2