Содержание
- 2. Введение ПРОБЛЕМА: Учащиеся не всегда умеют сознательно использовать информацию об иррациональных уравнениях. Грамотно применять свойства корней
- 3. " Посредством уравнений, теорем Я уйму всяких разрешал проблем" (Чостер, английский поэт, средние века) "Уравнение -
- 4. Ход урока Организация урока. (1мин.) Постановка целей, принятие их учащимися.(2 мин.) Вопрос, раскрывающий сущность проблемы. Дискуссия
- 5. Начало урока Здравствуйте! Надеюсь ,что у вас серьезный настрой на урок. Желаю вам высоких результатов. В
- 6. 2.Вопрос - проблема Какой шаг в решении уравнения приводит к появлению лишних корней.
- 7. Найди ошибку. 16 -36 =25 – 45 16-36+20,25=25-45+20,25 (4-4,5)² =(5-4,5)² 4-4,5=5-4,5 4=5 Вывод: Если квадраты двух
- 8. 3. Изучение нового материала. Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Устно: какие
- 9. 4. Первичное осмысление. √ х – 6 = 2 √ х – 3 = 0 √
- 10. Алгоритм решения уравнений. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения
- 11. 5. Закрепление изученного материала. Является ли число x корнем уравнения: а) √ х – 2 =
- 12. Решим уравнение: √ х + 2 = х Решение: х + 2 = х2, х2 –
- 13. Решим уравнение. √2х – 3 = √ х - 2
- 14. Решение Возведем обе части уравнения в квадрат, получим: 2х -3 = х -2 , х =
- 15. История неразумных чисел История иррациональных чисел относится к удивительному открытию пифагорийцев. А началось это с простого
- 16. 6. Задание на дом. № 900 ( г, д, е ) № 901 ( а, г
- 18. Скачать презентацию











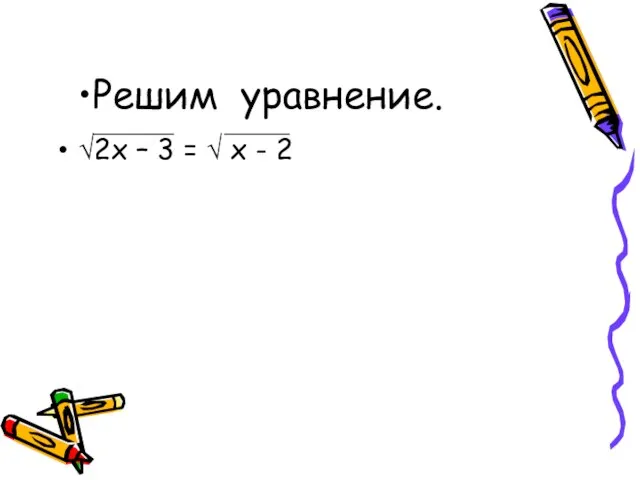



 Предложение по перспективному развитию военного городка отдельного медико-санитарного батальона г. Балашиха
Предложение по перспективному развитию военного городка отдельного медико-санитарного батальона г. Балашиха Язык современной Интернет - субкультуры
Язык современной Интернет - субкультуры Отцовская доблесть. Семья Канчуриных
Отцовская доблесть. Семья Канчуриных Кто хочет стать миллионером (разовая игра 15 вопросов)
Кто хочет стать миллионером (разовая игра 15 вопросов) Публичный отчет МОУ СОШ №18 г. Пензы (декабрь 2009 г.)
Публичный отчет МОУ СОШ №18 г. Пензы (декабрь 2009 г.) Презентация на тему Декартовы координаты
Презентация на тему Декартовы координаты  Кулинарные традиции семьи
Кулинарные традиции семьи Аксонометрия. Прямоугольные и косоугольные аксонометрические проекции
Аксонометрия. Прямоугольные и косоугольные аксонометрические проекции Технические средства измерения массы груза
Технические средства измерения массы груза Мой любимый продукт
Мой любимый продукт Гамма-стерилизация
Гамма-стерилизация Химическое оружие. Виды
Химическое оружие. Виды ОРГАНИЗАЦИЯ ПРОЦЕССА ОБУЧЕНИЯ В ПОЛЬШЕ
ОРГАНИЗАЦИЯ ПРОЦЕССА ОБУЧЕНИЯ В ПОЛЬШЕ Служба в органах уголовно-исполнительной системы как вид государственной службы
Служба в органах уголовно-исполнительной системы как вид государственной службы Путевая бюрократия или все о вагонной документации
Путевая бюрократия или все о вагонной документации Ecological problems
Ecological problems Продам 2 комнатную квартиру по приятной цене
Продам 2 комнатную квартиру по приятной цене Возрастная психология
Возрастная психология Правила vs Нормы
Правила vs Нормы Психолог-юзабилист О новой профессии в мире высоких технологий (для студентов-психологов)
Психолог-юзабилист О новой профессии в мире высоких технологий (для студентов-психологов) Управления рисками в банке
Управления рисками в банке Презентация на тему Мировые религии
Презентация на тему Мировые религии Ядерная сделка с Ираном
Ядерная сделка с Ираном Lean Startup «Бережливый стартап» Как делать игры, нужные людям
Lean Startup «Бережливый стартап» Как делать игры, нужные людям Презентация на тему Первые летательные аппараты
Презентация на тему Первые летательные аппараты Документирование среды программирования для операционной системы L4Ka(Documenting the programmer environment for L4ka)
Документирование среды программирования для операционной системы L4Ka(Documenting the programmer environment for L4ka) Правописание частицы НЕ с глаголами
Правописание частицы НЕ с глаголами Пьеса для театра А.Н.Островского "Снегурочка"
Пьеса для театра А.Н.Островского "Снегурочка"