Содержание
- 2. График функции y = ax2. График функции y = ax2 + bx + c. Лабораторно-графическая работа
- 3. у х 0 x ≤ 0 x ≥ 0 y = ax2, a>0 y = ax2,
- 4. Задача: Построить график функции y = x2 – 2x + 3 и сравнить с графиком функции
- 5. у х 0 y = ax2+bx+c, a>0 y = ax2+bx+c, a Графиком функции y = ax2+bx+c
- 6. Задания Дана функция y = ax2 +bx + c. Найдите координаты точек пересечения графика функции с
- 8. Скачать презентацию
Слайд 3у
х
0
x ≤ 0
x ≥ 0
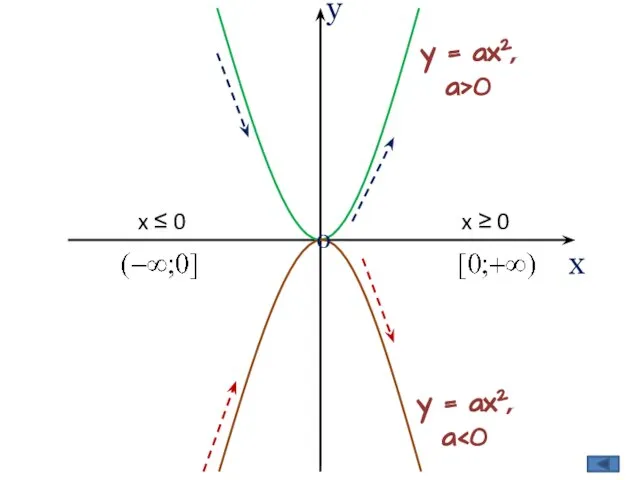
y = ax2, a>0
y = ax2, a<0
у
х
0
x ≤ 0
x ≥ 0
y = ax2, a>0
y = ax2, a<0
Слайд 4Задача: Построить график функции y = x2 – 2x + 3 и
Задача: Построить график функции y = x2 – 2x + 3 и

сравнить с графиком функции y = x2
Построение.
Графиком функции y = x2 – 2x + 3 является парабола, ветви которой направлены вверх.
Составим таблицу значений функции y = x2 – 2x + 3
Построим график функции y = x2 – 2x + 3
Сравним графики y = x2 – 2x + 3 и y = x2
y = x2 – 2x + 3 = x2 – 2x + 1+ 2 = (x – 1)2 + 2
Вывод: Графиком функции y = x2 – 2x + 3 является парабола, получаемая сдвигом параболы y = x2 на единицу вправо и на две единицы вверх.
Слайд 5у
х
0
y = ax2+bx+c, a>0
y = ax2+bx+c, a<0
Графиком функции
y = ax2+bx+c является
у
х
0
y = ax2+bx+c, a>0
y = ax2+bx+c, a<0
Графиком функции
y = ax2+bx+c является
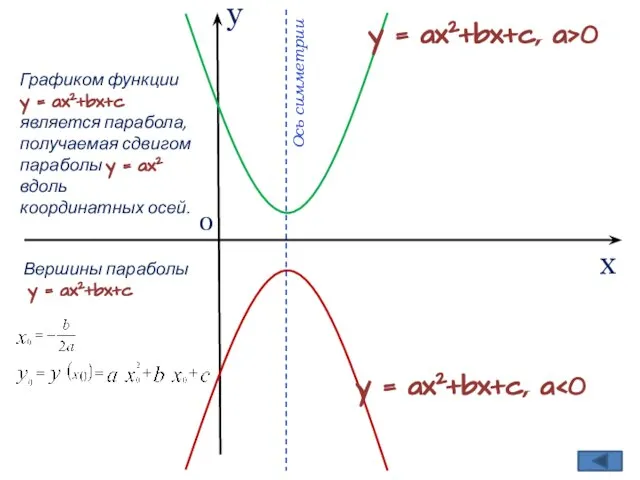
парабола, получаемая сдвигом параболы y = ax2 вдоль координатных осей.
Вершины параболы
y = ax2+bx+c
Ось симметрии
Слайд 6Задания
Дана функция y = ax2 +bx + c.
Найдите координаты точек пересечения графика
Задания
Дана функция y = ax2 +bx + c.
Найдите координаты точек пересечения графика

функции с осями координат.
Постройте график данной функции.
С помощью графика найдите:
множество значений х, на котором функция:
1) возрастает, 2) убывает, 3) принимает положительные значения, 4) принимает отрицательные значения;
значения переменной х, при которых функция принимает наибольшее и наименьшее значение.
Проходит ли график данной функции через точки A(m; n), B(-m; n), C(-m; -n), D(m; -n).
Постройте график данной функции.
С помощью графика найдите:
множество значений х, на котором функция:
1) возрастает, 2) убывает, 3) принимает положительные значения, 4) принимает отрицательные значения;
значения переменной х, при которых функция принимает наибольшее и наименьшее значение.
Проходит ли график данной функции через точки A(m; n), B(-m; n), C(-m; -n), D(m; -n).
- Предыдущая
Параллелограмм ВариньонаСледующая -
Ломаные
 Социально-педагогическое проектирование, как форма инновационной технологии в деятельности социального педагога
Социально-педагогическое проектирование, как форма инновационной технологии в деятельности социального педагога ФГУП «Комбинат Питания «Кремлевский» Предлагает организацию банкетных мероприятий в г. Сочина территории « санатория «Русь»З
ФГУП «Комбинат Питания «Кремлевский» Предлагает организацию банкетных мероприятий в г. Сочина территории « санатория «Русь»З Урок русского языка в 6 классе Учитель МОУ «Лицей №21»Власова И.Л.
Урок русского языка в 6 классе Учитель МОУ «Лицей №21»Власова И.Л. Рейганоміка.Тетчеризм
Рейганоміка.Тетчеризм Клубный дворик
Клубный дворик Орнаменты в национальном костюме
Орнаменты в национальном костюме Тела вращения
Тела вращения Повышение потребительского доверия в банковском секторе Таджикистана
Повышение потребительского доверия в банковском секторе Таджикистана Architecture Styles in America
Architecture Styles in America  Классификация фирусов
Классификация фирусов Юджин Смит
Юджин Смит Зерноуборочный комбайн ACROS 590 Plus
Зерноуборочный комбайн ACROS 590 Plus Водные походы и обеспечение безопасности на воде
Водные походы и обеспечение безопасности на воде Особенности строения животной клетки
Особенности строения животной клетки Проект модели стажировочной площадки: «Дошкольное образование: интеллектуальный ресурс развития нации. Одаренные дети. Поддержк
Проект модели стажировочной площадки: «Дошкольное образование: интеллектуальный ресурс развития нации. Одаренные дети. Поддержк Зимние Олимпийские игры
Зимние Олимпийские игры О внедрении федеральных государственных образовательных стандартов общего образования
О внедрении федеральных государственных образовательных стандартов общего образования В русской избе
В русской избе Новогоднее путешествие Владислава Сазыкина
Новогоднее путешествие Владислава Сазыкина Презентация на тему Методика Марии Монтессори
Презентация на тему Методика Марии Монтессори МРСК Сибири – студентам
МРСК Сибири – студентам Отрезные круги по металлу «СИБРТЕХ» Уважаемые партнёры! Компания «Мир Инструмента» представляет вашему вниманию линейку отрезны
Отрезные круги по металлу «СИБРТЕХ» Уважаемые партнёры! Компания «Мир Инструмента» представляет вашему вниманию линейку отрезны Энергоаудит насосных, вентиляторных и компрессорных установок
Энергоаудит насосных, вентиляторных и компрессорных установок Эффективная транспортная система, основанная на потребностях рынка
Эффективная транспортная система, основанная на потребностях рынка Сантехнические работы
Сантехнические работы Застывшие звуки
Застывшие звуки Как ткани ткут и нити прядут
Как ткани ткут и нити прядут Маленькие рыцари
Маленькие рыцари