Содержание
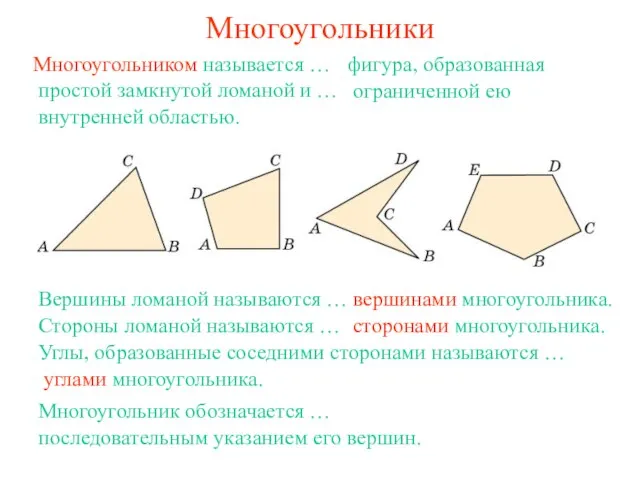
- 2. Многоугольники Многоугольником называется … фигура, образованная простой замкнутой ломаной и … вершинами многоугольника. Вершины ломаной называются
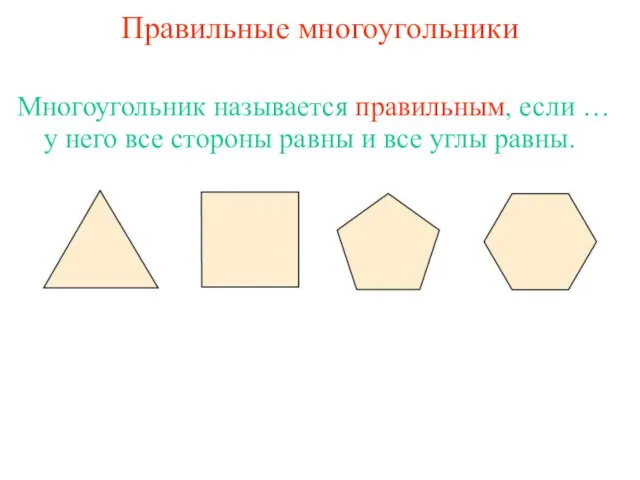
- 3. Правильные многоугольники у него все стороны равны и все углы равны. Многоугольник называется правильным, если …
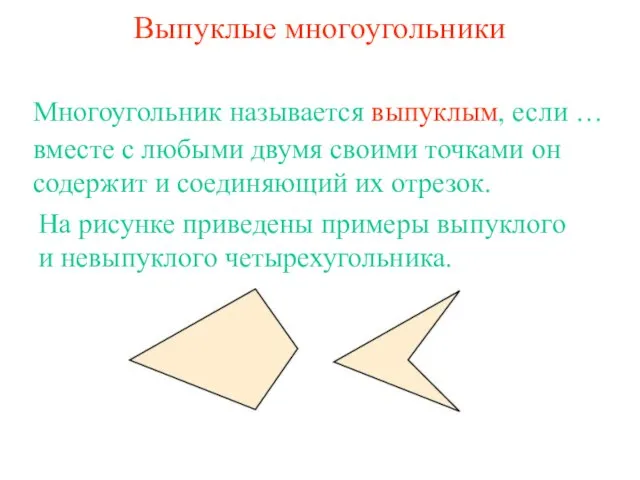
- 4. Выпуклые многоугольники вместе с любыми двумя своими точками он содержит и соединяющий их отрезок. Многоугольник называется
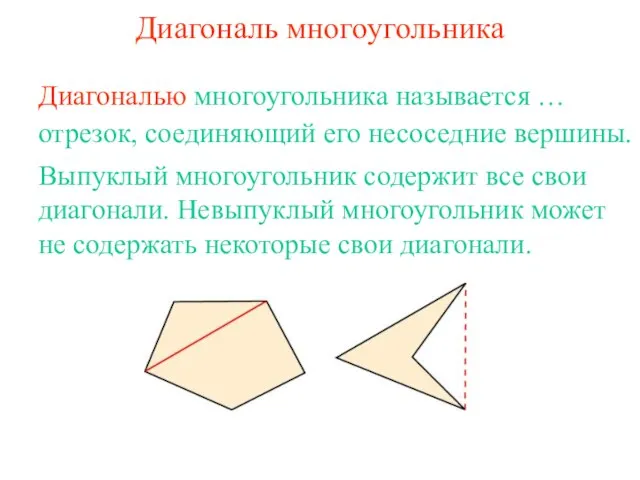
- 5. Диагональ многоугольника отрезок, соединяющий его несоседние вершины. Диагональю многоугольника называется … Выпуклый многоугольник содержит все свои
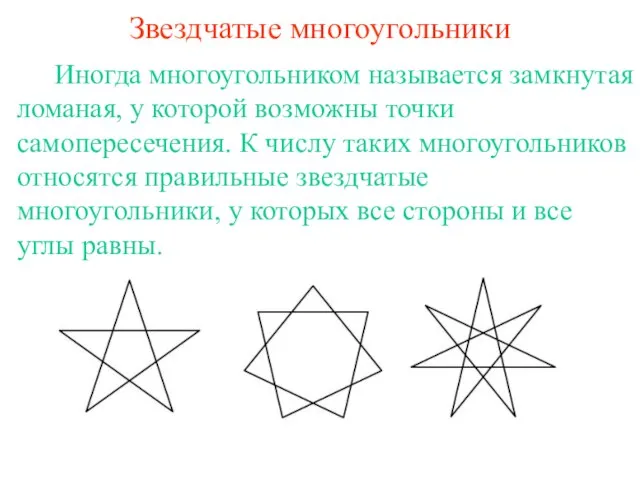
- 6. Звездчатые многоугольники Иногда многоугольником называется замкнутая ломаная, у которой возможны точки самопересечения. К числу таких многоугольников
- 7. Вопрос 1 Что называется ломаной, сторонами и вершинами ломаной? Ответ: Ломаной называется фигура, образованная конечным набором
- 8. Вопрос 2 Как обозначается ломаная? Ответ: Ломаная обозначается последовательным указанием ее вершин.
- 9. Вопрос 3 Что называется длиной ломаной? Ответ: Длиной ломаной называется сумма длин ее сторон.
- 10. Вопрос 4 Какая ломаная называется простой? Ответ: Ломаная называется простой, если она не имеет точек самопересечения
- 11. Вопрос 5 Какая ломаная называется замкнутой? Ответ: Ломаная называется замкнутой, если начало первого отрезка ломаной совпадает
- 12. Вопрос 6 Какая ломаная называется простой замкнутой? Ответ: Простой замкнутой ломаной называется замкнута ломаную, у которой
- 13. Вопрос 7 На сколько частей разбивает плоскость простая замкнутая ломаная? Ответ: Простая замкнутая ломаная разбивает плоскость
- 14. Вопрос 7 Какая фигура называется многоугольником? Что называется: вершинами; сторонами; углами многоугольника? Ответ: Фигура, образованная простой
- 15. Вопрос 8 Какой многоугольник называется n-угольником? Ответ: n – угольником называется многоугольник, у которого n углов.
- 16. Вопрос 9 Какой многоугольник называется правильным? Ответ: Многоугольник называется правильным, если у него все стороны равны
- 17. Вопрос 10 Какой многоугольник называется выпуклым? Ответ: Многоугольник называется выпуклым, если вместе с любыми двумя своими
- 18. Вопрос 11 Что называется диагональю многоугольника? Ответ: Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.
- 19. Упражнение 1 Незамкнутая ломаная имеет 10 вершин. Сколько у нее сторон? Ответ: 9.
- 20. Упражнение 2 Замкнутая ломаная имеет 20 сторон. Сколько у нее вершин? Ответ: 20.
- 21. Упражнение 3 Укажите, какие фигуры, изображенные на рисунке, являются простыми ломаными. Ответ: 1, 2, 3, 5,
- 22. Упражнение 4 Верно ли, что любая замкнутая ломаная разбивает плоскость на две области? Ответ: Нет.
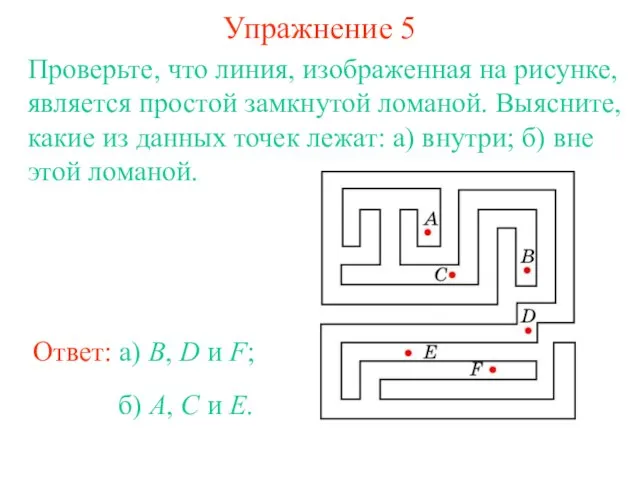
- 23. Упражнение 5 Проверьте, что линия, изображенная на рисунке, является простой замкнутой ломаной. Выясните, какие из данных
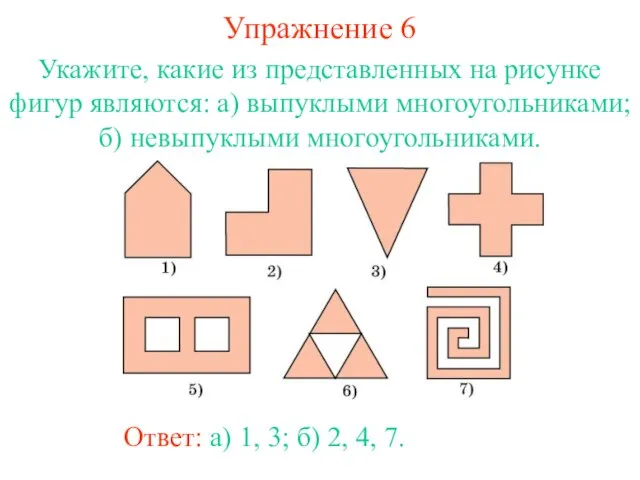
- 24. Упражнение 6 Укажите, какие из представленных на рисунке фигур являются: а) выпуклыми многоугольниками; б) невыпуклыми многоугольниками.
- 25. Упражнение 7 Какая имеется зависимость между числом вершин и числом сторон многоугольника? Ответ: Число вершин равно
- 26. Упражнение 8 Сколько диагоналей имеет: а) треугольник? 0; б) четырехугольник? 2; в) пятиугольник? 5; г) шестиугольник?
- 27. Упражнение 9 Может ли многоугольник иметь ровно: а) 10 диагоналей? нет; б) 20 диагоналей? да; в)
- 28. Упражнение 10 Существует ли многоугольник, число диагоналей которого равно числу его сторон? Ответ: Да, пятиугольник.
- 29. Упражнение 11 Выпуклый многоугольник имеет 35 диагоналей. Сколько у него сторон? Ответ: 10.
- 30. Упражнение 12 На сколько треугольников делится выпуклый: а) 4-угольник; б) 5-угольник; в) 6-угольник; г)* n-угольник своими
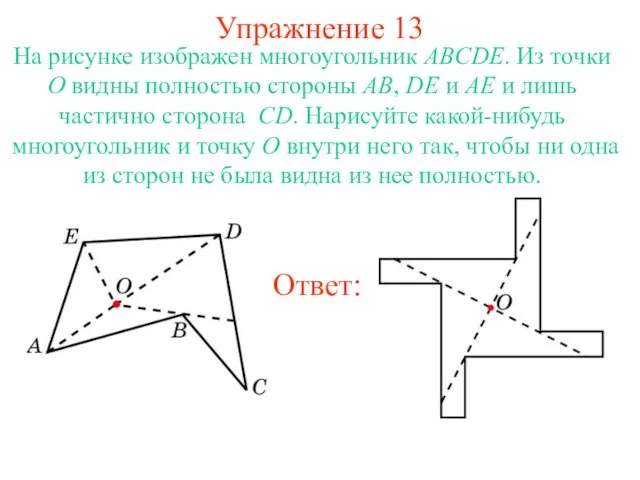
- 31. Упражнение 13 На рисунке изображен многоугольник ABCDE. Из точки O видны полностью стороны AB, DE и
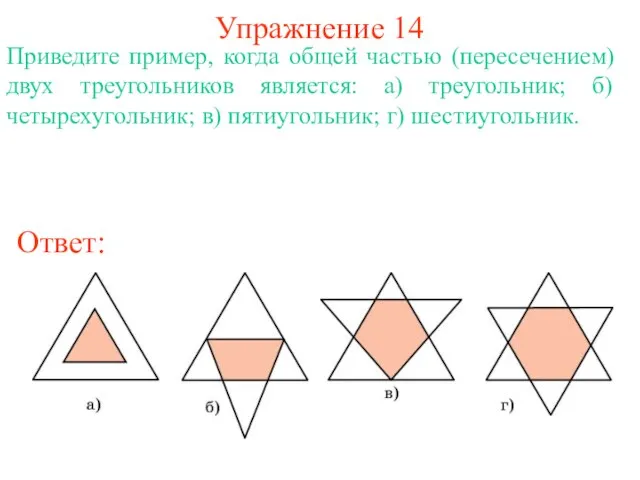
- 32. Упражнение 14 Приведите пример, когда общей частью (пересечением) двух треугольников является: а) треугольник; б) четырехугольник; в)
- 33. Упражнение 15 Может ли пересечением двух треугольников быть семиугольник? Ответ: Нет.
- 35. Скачать презентацию























 Современное облагораживание драгоценных рубинов и сапфиров
Современное облагораживание драгоценных рубинов и сапфиров Определение машины Тьюринга
Определение машины Тьюринга Понятие «средний»
Понятие «средний» Образ Усть-Сысольска
Образ Усть-Сысольска Рисуем портрет мамы
Рисуем портрет мамы plakat2
plakat2 Интегрированный фестиваль творчества Путь к успеху
Интегрированный фестиваль творчества Путь к успеху Подборка книг по финансовой грамотности
Подборка книг по финансовой грамотности Поведенческие реакции в стрессе
Поведенческие реакции в стрессе Мусаева Алина..Мк-19-2р
Мусаева Алина..Мк-19-2р Презентация на тему Мастер-класс по педагогическим технологиям
Презентация на тему Мастер-класс по педагогическим технологиям Измерение информации 9 класс
Измерение информации 9 класс Презентация на тему Понятие, признаки, функции социального партнерства
Презентация на тему Понятие, признаки, функции социального партнерства  Парк мечты.
Парк мечты. Устройство компьютера
Устройство компьютера Презентация на тему Диктанты-предложения при подготовке к ЕГЭ 10-11 класс
Презентация на тему Диктанты-предложения при подготовке к ЕГЭ 10-11 класс Псалом 85, молитва Давида
Псалом 85, молитва Давида Духовная сфера общества
Духовная сфера общества Module_3f_s_52_Word_formation
Module_3f_s_52_Word_formation Притчи
Притчи Социальная среда подростка
Социальная среда подростка Дымковская игрушка
Дымковская игрушка Youtube
Youtube Йогурт
Йогурт Летняя математическая школа
Летняя математическая школа Мезенская роспись
Мезенская роспись ИННОВАЦИОННАЯ РОЛЬ НАУЧНО-ОБРАЗОВАТЕЛЬНОГО КОМПЛЕКСА В ОБЕСПЕЧЕНИИ ЭНЕРГОЭФФЕКТИВНОСТИ ОТРАСЛЕЙ ТЭК
ИННОВАЦИОННАЯ РОЛЬ НАУЧНО-ОБРАЗОВАТЕЛЬНОГО КОМПЛЕКСА В ОБЕСПЕЧЕНИИ ЭНЕРГОЭФФЕКТИВНОСТИ ОТРАСЛЕЙ ТЭК Спортивные сборы по хоккею в Бресте
Спортивные сборы по хоккею в Бресте