Лекции по физике. Молекулярная физика и основы термодинамики

Обратимые и необратимые процессы
Обратимым называют процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения
Обратимым может быть лишь равновесный процесс, но не всякий равновесный процесс обратим

Обратимые и необратимые процессы
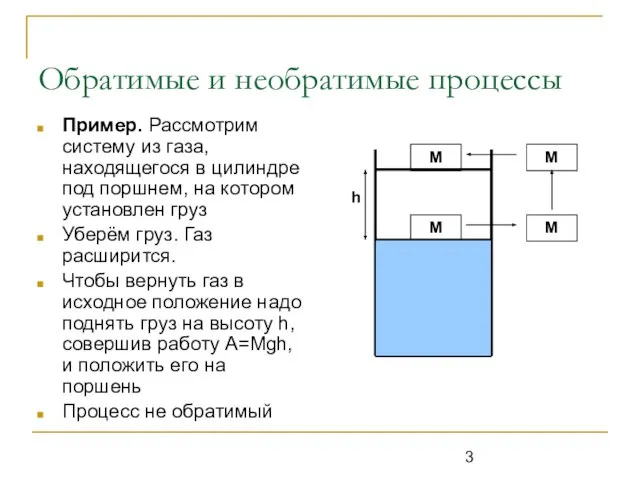
Пример. Рассмотрим систему из газа, находящегося в цилиндре под поршнем, на котором установлен груз
Уберём груз. Газ расширится.
Чтобы вернуть газ в исходное положение надо поднять груз на высоту h, совершив работу A=Mgh, и положить его на поршень
Процесс не обратимый

Обратимые и необратимые процессы
Разобьём груз на две равных части
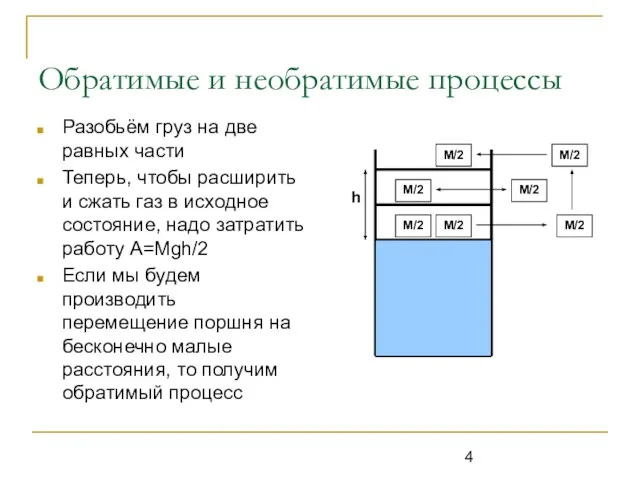
Теперь, чтобы расширить и сжать газ в исходное состояние, надо затратить работу A=Mgh/2
Если мы будем производить перемещение поршня на бесконечно малые расстояния, то получим обратимый процесс

Обратимые и необратимые процессы
Пример равновесного необратимого процесса – теплообмен
Компенсацией за осуществление необратимых круговых процессов является перевод энергии из одной формы в другую. В этом проявляется неэквивалентность различных форм энергии
Тепловая энергия оказывается менее ценным видом энергии, чем другие

Второе начало термодинамики
Второе начало термодинамики констатирует неэквивалентность различных видов энергии. Оно постулирует направление протекания тепловых процессов
Формулировка Клаузиуса: Теплота не может самопроизвольно переходить от тела менее нагретого к более нагретому

Второе начало термодинамики
Формулировка Томсона. Невозможен круговой процесс, единственным результатом которого было бы совершение работы за счёт охлаждения теплового резервуара
Устройство, которое позволяло бы осуществлять этот процесс, называется вечным двигателем второго рода

Второе начало термодинамики
Второе начало Т.Д. накладывает запрет на вечный двигатель второго рода
Из второго начала Т.Д. можно получить множество конкретных результатов с помощью метода циклов и метода термодинамических функций

Тепловые двигатели
Тепловой двигатель – это устройство, в котором совершается циклический Т.Д. процесс
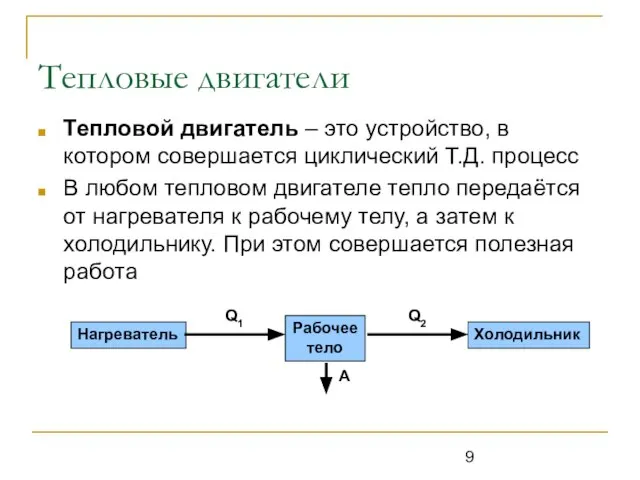
В любом тепловом двигателе тепло передаётся от нагревателя к рабочему телу, а затем к холодильнику. При этом совершается полезная работа

Тепловые двигатели

Метод циклов
В циклическом процессе ΔU=0 → Q=A=Q1-Q2
При переходе 1→2 работа совершается системой, а при переходе 2→1 над системой
При переходе 1'→2‘ тепло передаётся системе, а при переходе 2'→1' от системы
КПД теплового двигателя η=A/Q1=(Q1-Q2)/Q1

Цикл Карно
Цикл Карно состоит из двух изотерм и двух адиабат
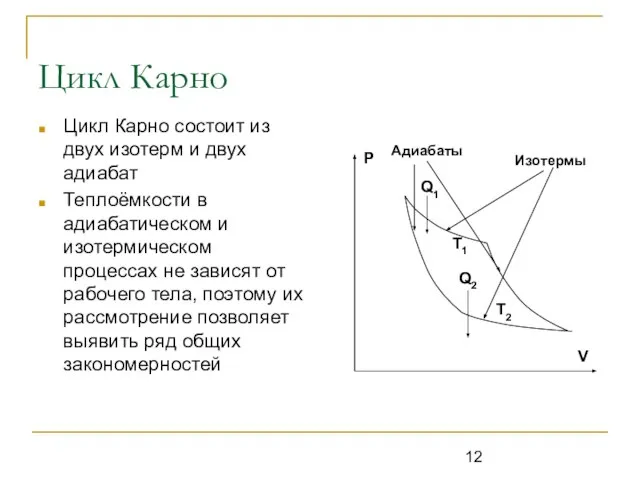
Теплоёмкости в адиабатическом и изотермическом процессах не зависят от рабочего тела, поэтому их рассмотрение позволяет выявить ряд общих закономерностей

Цикл Карно
Первая теорема Карно: Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника и не зависит от устройства машины и типа рабочего тела

Цикл Карно
Для идеального газа:
Q1=RT1ln(V2/V1)
Q2=RT2ln(V4/V3)
A=Q1-Q2=RT1ln(V2/V1)-RT2ln(V3/V4)
η=A/Q1=[RT1ln(V2/V1)-RT2ln(V3/V4)]/RT1ln(V2/V1)
Из уравнения адиабаты:
TVγ-1=const

Цикл Карно
T1V1γ-1= T2V4γ-1 и T1V2γ-1= T2V3γ-1 →
V2/V1=V3/V4 →
η=(T1-T2)/T1=1-T2/T1
Для повышения КПД надо повышать температуру нагревателя и понижать температуру холодильника
η=(Q1-Q2)Q1=(T1-T2)/T1 →
Q1/T1=Q2/T2
Величина Q/T называется приведённой теплотой

Цикл Карно
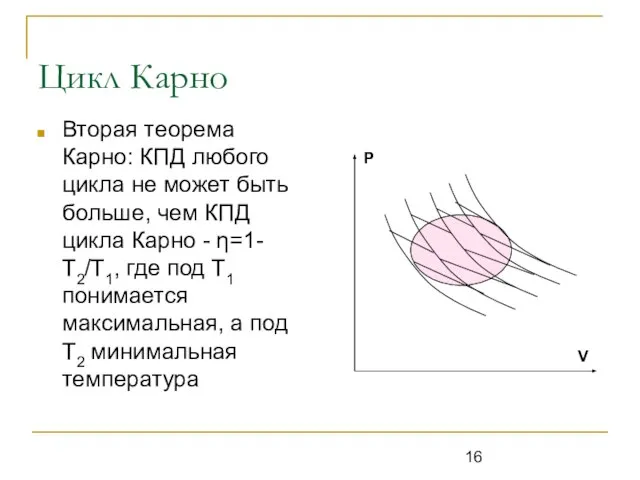
Вторая теорема Карно: КПД любого цикла не может быть больше, чем КПД цикла Карно - η=1-Т2/Т1, где под Т1 понимается максимальная, а под Т2 минимальная температура

Энтропия
Рассмотрим произвольный равновесный цикл. Аппроксимируем его малыми циклами Карно
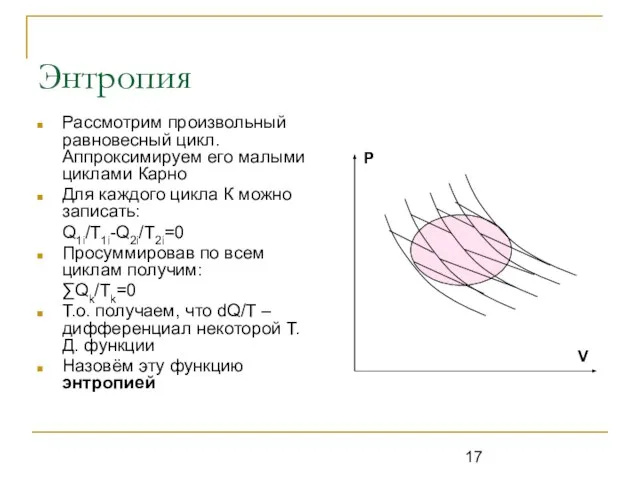
Для каждого цикла К можно записать:
Q1i/T1i-Q2i/T2i=0
Просуммировав по всем циклам получим:
∑Qk/Tk=0
Т.о. получаем, что dQ/T – дифференциал некоторой Т.Д. функции
Назовём эту функцию энтропией

Энтропия
Энтропия – это такая функция состояния, дифференциал которой связан с элементарным тепловым эффектом в обратимом процессе соотношением:
dQ=TdS (*)
Энтропия S имеет размерность теплоёмкости
С учётом (*) первое начало Т.Д. можно выразить как:
TdS=dU+PdV
Отсюда, зная термическое и калорическое уравнения, состояния можно найти зависимость энтропии от Т.Д. параметров

Энтропия
Найдём энтропию идеального газа
Из dU=cVdT и P/T=R/V следует что:
dS=cVdT/T+RdV/V → S(T,V)=cVlnT+RlnV
при cV=const
Можно S выразить через T и P:
S(T,P)=cPlnT-RlnP

Энтропия
Определение энтропии через теплоту встречает одну трудность. В точке Т=0 интеграл ∫dQ/T может расходиться
Эта неопределённость устраняется постулатом Нернста, называемым иногда третьим началом термодинамики

Постулат Нернста
Постулат Нернста сводится к двум утверждениям:
При приближении к абсолютному нулю энтропия стремится к определённому конечному пределу. Можно положить S(Т=0)=0
Все равновесные процессы при Т=0 происходят без изменения энтропии. В частности, при Т=0 S не зависит от объёма

Статистическая интерпретация энтропии
Вероятность состояния пропорциональна его статистическому весу Ω, т.е. числу микроскопических способов, которым может быть осуществлено данное макросостояние
Разобьём некоторую Т.Д. систему на две подсистемы, которые находятся в состояниях со стат. весами Ω1 и Ω2
Число способов, которыми может реализоваться данное состояние системы:
Ω=Ω1⋅Ω2

Статистическая интерпретация энтропии
Т.о. логарифм стат. веса является аддитивной функцией состояния системы:
lnΩ=lnΩ1+lnΩ2
Энтропия системы:
S=k⋅lnΩ (**)
где k – постоянная Больцмана
Формула (**) называется формулой Больцмана

Статистическая интерпретация энтропии
Т.к. равновесным состоянием является состояние с наибольшим стат. весом (и наибольшей энтропией), то можно заключить, что при протекании необратимых процессов энтропия изолированной системы возрастает
Энтропия системы, находящейся в равновесном состоянии, максимальна

Статистическая интерпретация энтропии
При протекании обратимых процессов энтропия изолированной системы остаётся постоянной
Энтропия равновесной системы не остаётся строго постоянной она претерпевает флуктуации
Второй закон термодинамики, иногда называемый законом возрастания энтропии, утверждает, что энтропия изолированной системы может только возрастать либо оставаться неизменной:
ΔS≥0