Лекция 1. Множества. Элементы теории множеств. Принцип включения- исключения.

1. Множества
Совокупность объектов, определяемых некоторым свойством, присущим каждому из них, называется множеством.
Каждый объект, входящий в множество, называется его элементом, а свойство их объединяющее – характеристическим свойством множества.
Множества принято обозначать большими буквами латинского алфавита: A,B,C…, либо буквами с нижними индексами A1,A2 …, элементы множества – соответствующими малыми латинскими буквами.

Определение. Множество называется подмножеством множества , если каждый элемент множества является элементом множества .
Обозначение:
Каждое множество является подмножеством (несобственным) самого себя .
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается символом (квантором) .

Парадокс брадобрея.
В одном полку служил парикмахер. Однажды командир с целью экономии времени приказал ему брить только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, т.к. работы для него стало меньше. Но потом он задумался: а кто будет брить его самого?

Другая версия парадокса.
Прилагательное русского языка назовем рефлексивным, если оно обладает тем свойством, которое определяет. Например, прилагательное «русский» – рефлексивное, а прилагательное «английский» – нерефлексивное. Прилагательное «трехсложный» – рефлексивное (состоит из трех слогов). А прилагательное «четырехсложный» – нерефлексивное (состоит из пяти слогов).
Интересно: а прилагаемое «трудновыговариваемое» рефлексивно или нет?
Следовательно, все прилагательные можно разделить на два множества: рефлексивные и нерефлексивные прилагательные. Но рассмотрим само прилагательное «нерефлексивный». Оно рефлексивное или нет?

2. Операции над множествами
Определение. Объединением двух множеств и называется множество , элементами которого являются элементы, входящие в хотя бы в одно из данных множеств.

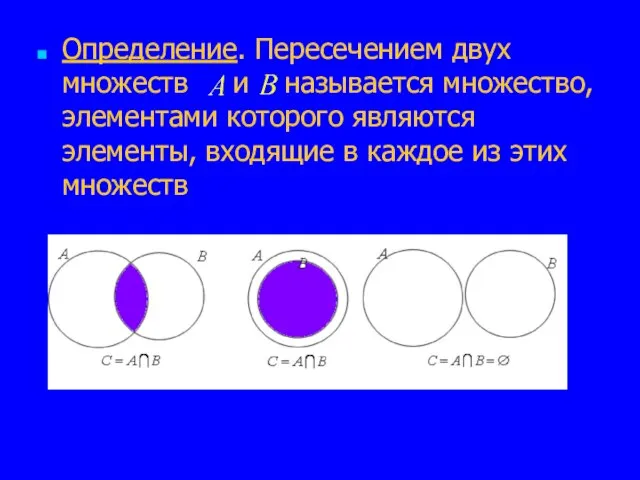
Определение. Пересечением двух множеств и называется множество, элементами которого являются элементы, входящие в каждое из этих множеств

3. Принцип включения-исключения
Принцип включения-исключения является важнейшим математическим инструментом в различных разделах математики: комбинаторике, теории вероятности, теории множеств.

Формула сложения
Если два множества состоят из конечного
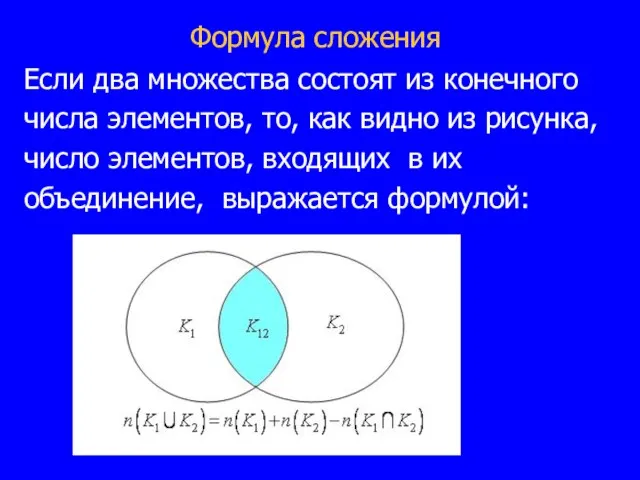
числа элементов, то, как видно из рисунка,
число элементов, входящих в их
объединение, выражается формулой:

Если же свойств три, то можно по аналогии определить множества

Задача 1.
На экзамене по математике были предложены 3 задачи: одна по алгебре, одна по геометрии, одна по тригонометрии. Из 1000 абитуриентов, решавших их, задачу по алгебре решили 800 человек, по геометрии – 700, а по тригонометрии – 600 человек. При этом задачи по алгебре и геометрии решили 600 абитуриентов, по алгебре и тригонометрии – 500, по геометрии и тригонометрии – 400. А 300 абитуриентов решили все три задачи. Сколько абитуриентов не решили ни одной задачи?

Задача 2
Из 100 опрошенных студентов филологического факультета 24 не изучают ни английский, ни немецкий, ни французский языки, 48 человек изучали английский, 8 – английский и немецкий, 26 – французский, 8 – французский и английский, 13 – французский и немецкий, 28 – немецкий. Сколько среди опрошенных студентов изучают английский, французский и немецкий языки одновременно?