Содержание
- 2. Анализ изображений Темы этой лекции Выделение краев Градиент изображения Алгоритм Canny Работа с контурами Цепные коды
- 3. Выделение краев Цель – преобразовать изображение в набор кривых для: выделения существенных характеристик сокращения объема информации
- 4. Выделение краев
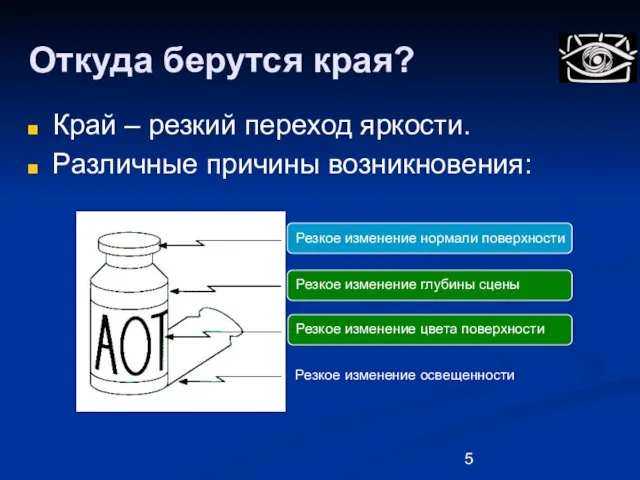
- 5. Откуда берутся края? Край – резкий переход яркости. Различные причины возникновения: Резкое изменение глубины сцены Резкое
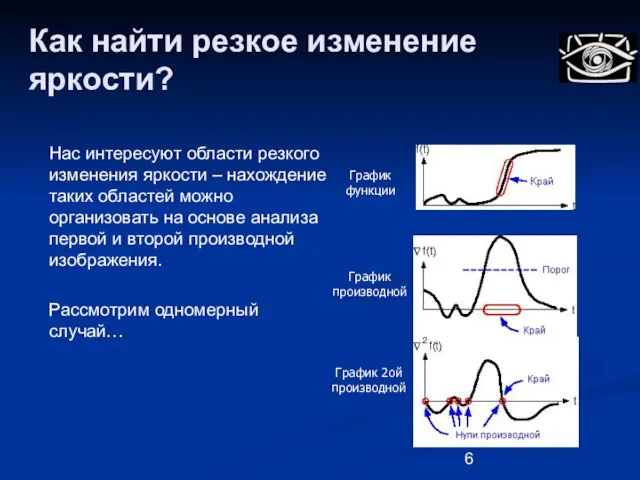
- 6. Как найти резкое изменение яркости? Нас интересуют области резкого изменения яркости – нахождение таких областей можно
- 7. Как найти резкое изменение яркости? Известно, что наибольшее изменение функции происходит в направлении ее градиента. Величина
- 8. Градиент яркости изображения Известно, что наибольшее изменение функции происходит в направлении ее градиента Приведем примеры…
- 9. Градиент яркости изображения Направление градиента задается: «Направление края» задается перпендикулярным градиенту «Сила края» задается абсолютной величиной
- 10. Вычисление градиента яркости изображения Математический смысл – приближенное вычисление производных по направлению Робертса Превитт Собеля Семейство
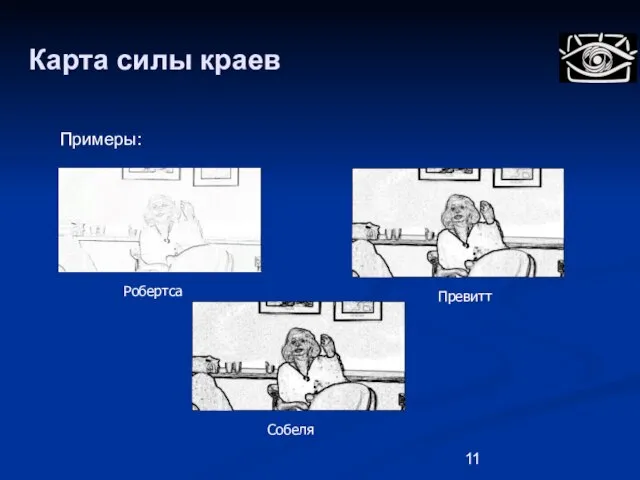
- 11. Карта силы краев Примеры: Робертса Превитт Собеля
- 12. Выделение краев Вычисление градиента – это еще не всё… Чего не хватает? Точности – края «толстые»
- 13. Выделение краев Нужно: Убрать слабые края и шум Сделать края тонкими Объединить пиксели краев в связные
- 14. Алгоритм Canny Давно придуман, однако до сих пор широко используется Шаги: Убрать шум и лишние детали
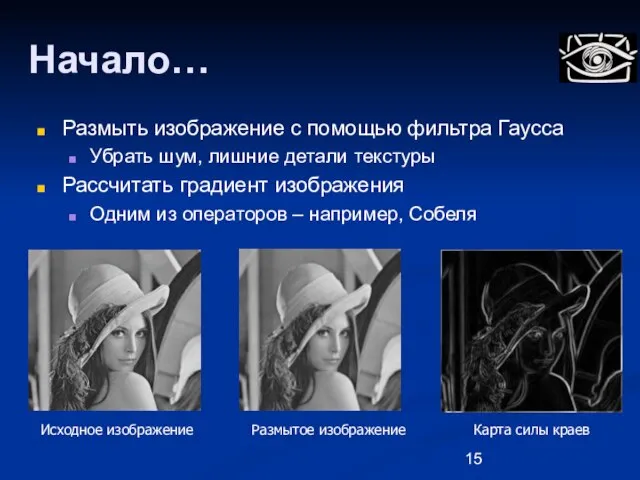
- 15. Начало… Размыть изображение с помощью фильтра Гаусса Убрать шум, лишние детали текстуры Рассчитать градиент изображения Одним
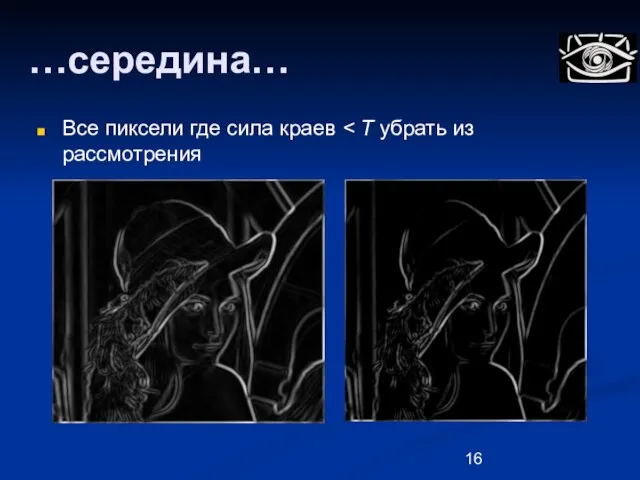
- 16. …середина… Все пиксели где сила краев
- 17. …середина… Поиск локальных максимумов Проверяя – является ли пиксель локальным максимумом вдоль направления градиента Приходится интерполировать
- 18. … финал Выбираем еще не обработанную точку локального максимума p в которой сила края Прослеживание края
- 19. Пояснения Как предсказать следующую точку края? От текущей точки шаг в сторону перпендикулярную градиенту В данном
- 20. Пояснения Для чего используются два порога? Чтобы уменьшить влияние шума для инициализации кривой используем больший порог
- 21. Алгоритм Canny Размыть изображение фильтром Гаусса c некоторым σ Убрать шум, лишние детали текстуры Рассчитать градиент
- 22. Canny - результат
- 23. Влияние σ (параметр фильтра Гаусса) Canny с Canny с исходное
- 24. Вопрос Получив контур объекта (связный набор пикселей) – как его дальше анализировать? Вариант - нужно преобразовать
- 25. Работа с контурами Полигональная аппроксимация Цепные коды Дескрипторы контуров
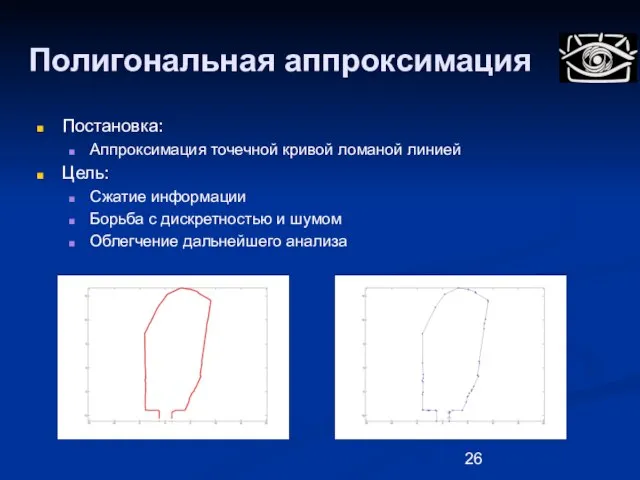
- 26. Полигональная аппроксимация Постановка: Аппроксимация точечной кривой ломаной линией Цель: Сжатие информации Борьба с дискретностью и шумом
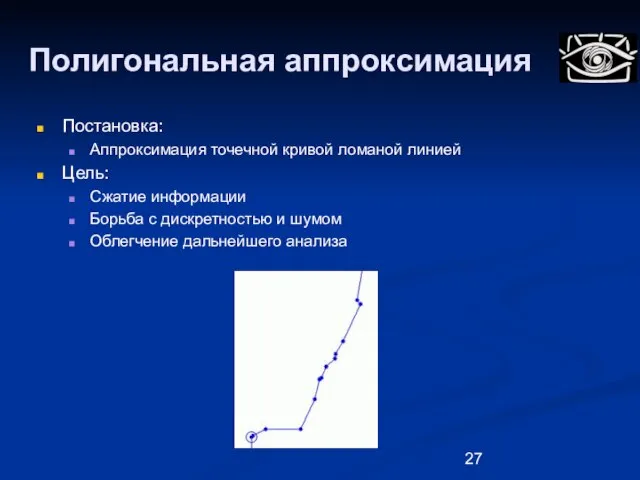
- 27. Полигональная аппроксимация Постановка: Аппроксимация точечной кривой ломаной линией Цель: Сжатие информации Борьба с дискретностью и шумом
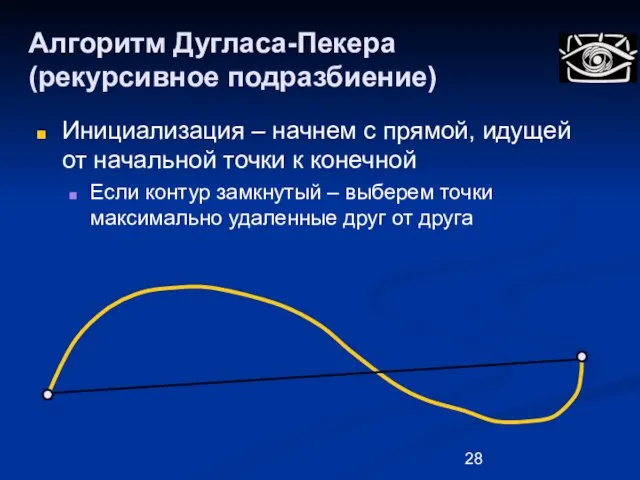
- 28. Алгоритм Дугласа-Пекера (рекурсивное подразбиение) Инициализация – начнем с прямой, идущей от начальной точки к конечной Если
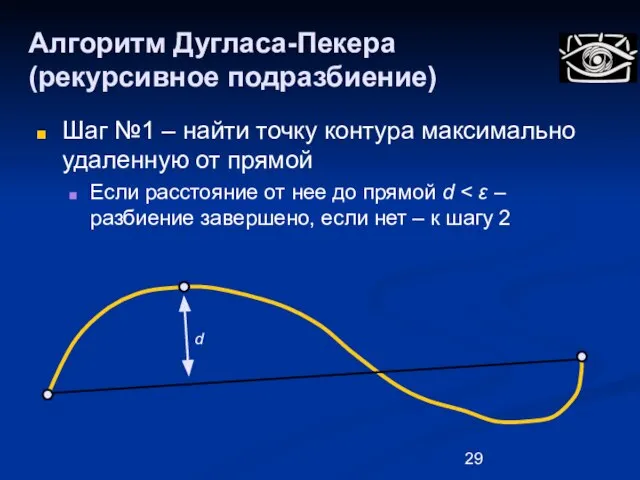
- 29. Алгоритм Дугласа-Пекера (рекурсивное подразбиение) Шаг №1 – найти точку контура максимально удаленную от прямой Если расстояние
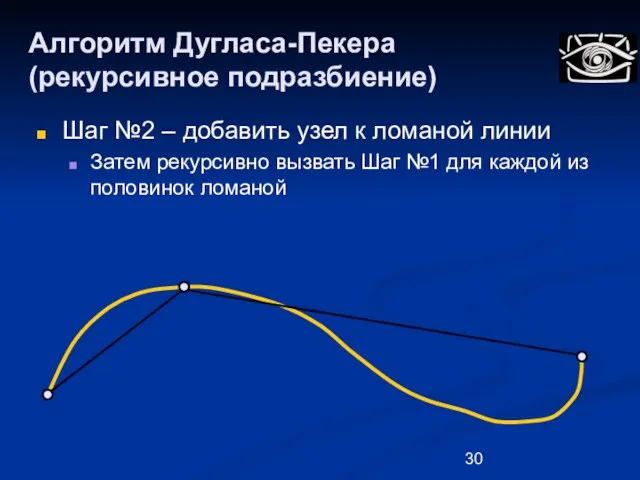
- 30. Алгоритм Дугласа-Пекера (рекурсивное подразбиение) Шаг №2 – добавить узел к ломаной линии Затем рекурсивно вызвать Шаг
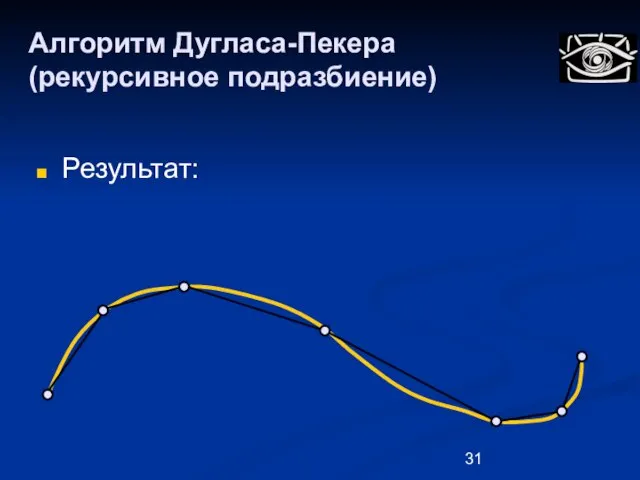
- 31. Алгоритм Дугласа-Пекера (рекурсивное подразбиение) Результат:
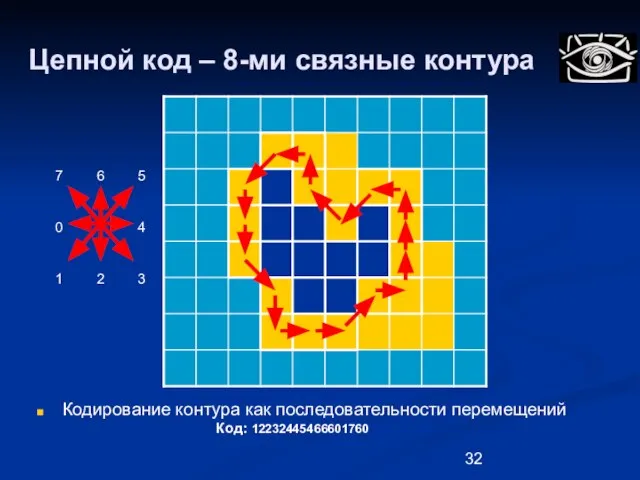
- 32. Цепной код – 8-ми связные контура Кодирование контура как последовательности перемещений Код: 12232445466601760
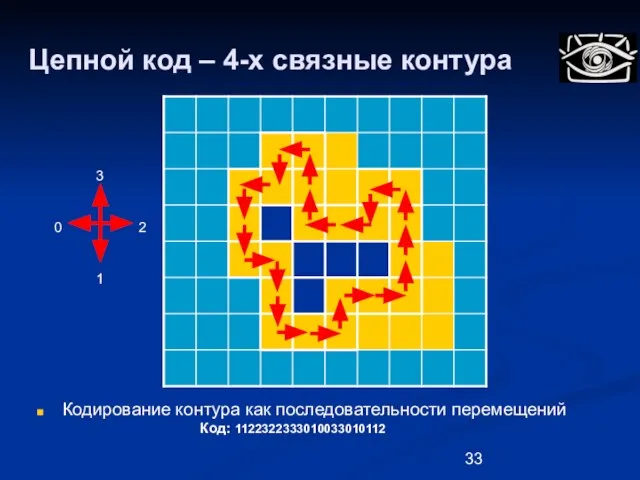
- 33. Цепной код – 4-х связные контура Кодирование контура как последовательности перемещений Код: 1122322333010033010112
- 34. Цепной код - свойства Свойства Цепной код – представление контура, независимое к его перемещению При замене
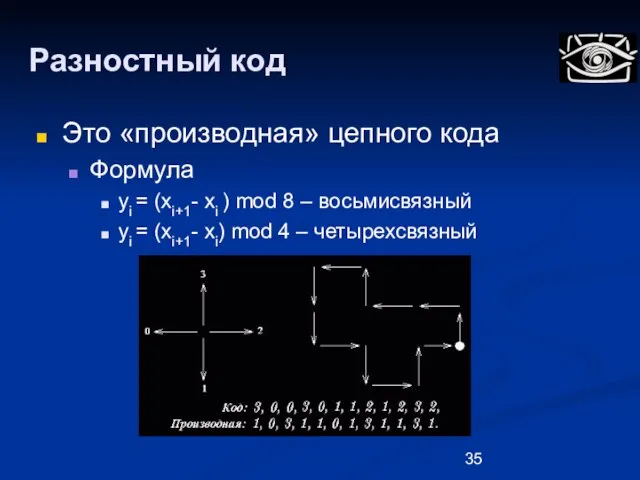
- 35. Разностный код Это «производная» цепного кода Формула yi = (xi+1- xi ) mod 8 – восьмисвязный
- 36. Разностный код Свойства: Инвариантен к повороту кратному 45 градусам (восьмисвязный) Проблемы: Также чувствителен к шуму Не
- 37. Ψ-s представление Аналогично считаем направление контура в каждой точке, но: Направление не ограничиваем точностью в 45
- 38. Ψ-s представление Обратите внимание: Результирующая функция ψ(s) зависит от длины дуги s (при движении «наискосок» она
- 39. Ψ-s представление NB на данном графике ось абсцисс – не длина дуги, а ее горизонтальная проекция
- 40. Ψ-s представление Свойства: Если нормировать полную длину к 1 – инвариантно к масштабу Несложным преобразованием можно
- 41. Кривизна Кривизна (curvature) – производная ψ(s) Аналогично разностному цепному коду, но со знаком Представление, инвариантное к
- 42. Дескрипторы Фурье Контур задается набором точек: Кол-во точек нормализуется к некоторому числу N Вычисляем коэффициенты дискретного
- 43. Дескрипторы Фурье Вычисляем амплитуды коэффициентов: Дескрипторы: Свойства: Инвариантны к переносу (вычли среднюю точку) Инвариантны к повороту
- 44. Признаки для распознавания контуров Цепной код (разностный код) Ψ-s представление Функция плотности наклона (slope density function)
- 45. Как вести прикладное исследование? Подготовительный этап Уяснить постановку задачи Собрать данные для проверки работы методов Провести
- 47. Скачать презентацию






























 Темперамент. Лекция № 2
Темперамент. Лекция № 2 Теорема Пифагора
Теорема Пифагора Строение скелета человека (8 класс)
Строение скелета человека (8 класс) Экономико-георгафическая характеристика Западной Европы
Экономико-георгафическая характеристика Западной Европы 300450
300450 Product placement 30-60
Product placement 30-60 Глагольная эмотивная лексика монгольского языка
Глагольная эмотивная лексика монгольского языка Устройства для обработки и передачи видеоизображения
Устройства для обработки и передачи видеоизображения Для чего вообще нужно ТЗ Формально: ТЗ это документ в котором перечислены все виды работ, которые выполняются в проекте, а также ука
Для чего вообще нужно ТЗ Формально: ТЗ это документ в котором перечислены все виды работ, которые выполняются в проекте, а также ука Работа с одаренными детьми в современных условиях
Работа с одаренными детьми в современных условиях Методическая система учителя как условие обеспечения качества образования
Методическая система учителя как условие обеспечения качества образования ПОРЯДОК аттестации педагогических работников
ПОРЯДОК аттестации педагогических работников Автопортрет Т.Г. Шевченко
Автопортрет Т.Г. Шевченко Искусство. Индивидуальность восприятия
Искусство. Индивидуальность восприятия Откуда есть пошла Русская земля
Откуда есть пошла Русская земля Шедевры родной литературы
Шедевры родной литературы Футбол без дискриминации
Футбол без дискриминации Нұртас 1.10
Нұртас 1.10 Фантастическая история
Фантастическая история История развития жизни
История развития жизни kakaya_byvaet_valyuta_chast_1
kakaya_byvaet_valyuta_chast_1 СОВАТА
СОВАТА 20.2
20.2 2010г.
2010г. «Квартира - Экспресс»
«Квартира - Экспресс» Презентация на тему Сандро Боттичелли
Презентация на тему Сандро Боттичелли  Айыҡ ауыл
Айыҡ ауыл Презентация на тему Викторина по ПДД
Презентация на тему Викторина по ПДД