Лекция_1 Магистры

Структура курса
1) 8 лекций и 17 практических занятий.
2) Контрольные мероприятия:
2 РК: 8 и 15 недели;
1 домашнее задание: 16 неделя;
модули: 10 и 17 недели.
3) Экзамен.

Программный комплекс ANSYS
Бесплатная лицензия для студентов:
http://http://www.ansys.com/products/academic/ansys-student
ANSYS Student - ANSYS Workbench с модулем ANSYS CFD.

Особенности установки ANSYS
Продукт поддерживается только на MS Windows 7, 8, 10 64-разрядных компьютерах.
Путь обращения программы к своим папкам или папкам, созданным пользователем, не должен иметь букв русского алфавита, т.е. все имена и названия – на англоязычной раскладке.
Текущая бесплатная студенческая версия имеет следующие ограничения на размер сетки:
1. Структурные задачи (деформация твердого тела) – 32 000 конечных элементов;
2. Гидро-газодинамика – 512 000 расчетных узлов сетки.

Литература
Флетчер К. Вычислительные методы в динамике жидкостей, 2 т.
Ландау Л. Д., Лифшиц Е .М. Теоретическая физика. Уч. пособие. Т. 6. Гидродинамика.
Роуч П. Вычислительная гидродинамика.
Лоханский Я.К. Основы вычислительной гидромеханики и тепломассообмена. Уч. пособие.
Электронный журнал для пользователей ANSYS [http://www.ansysadvantage.ru/]

Моделирование – процесс замещения объекта исследования некоторой его моделью и проведение исследований на модели с целью получения необходимой информации об объекте.
Модель – это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.
Достоинства моделирования:
– легкость и доступность получения информации;
– сокращение сроков исследования;
- поведение в любых мыслимых ситуациях;
– уменьшением материальных затрат на исследование.
Недостатки моделирования:
– невозможность учесть все свойства реального объекта (отбрасывание несущественных, упрощение).
Лекция 1. Математическое моделирование и вычислительный
эксперимент. Математическая модель.

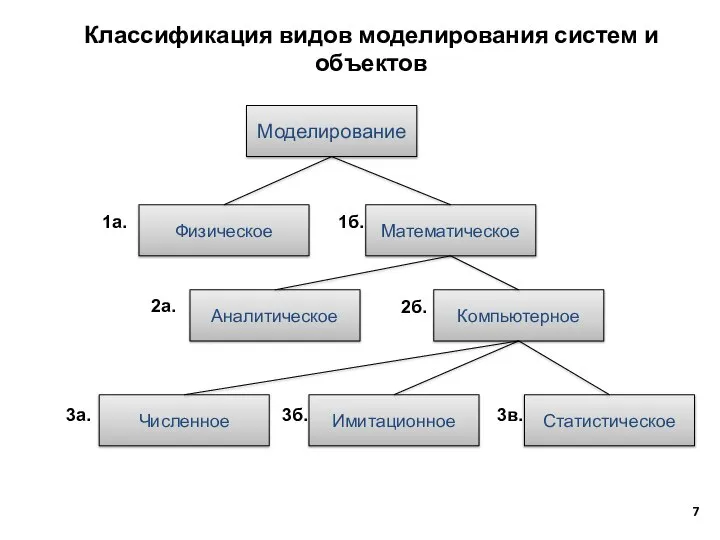
Классификация видов моделирования систем и объектов
Моделирование
Физическое
Математическое
Аналитическое
Компьютерное
Численное
Имитационное
Статистическое
1а.
2а.
3а.
2б.
1б.
3б.
3в.

1а. Физическое моделирование
Аэродинамическая труба Т-101
Размеры объектов испытаний:
размах крыла – 18 м;
длина фюзеляжа – 30 м;
площадь крыла – 35 м2

1б. Математическое моделирование
История математического моделирования
Первые методы Ньютона (численный метод решения алгебраических уравнений), Лагранжа, Эйлера (численный метод решения обыкновенных дифференциальных уравнений), аль-Хорезми ( среднеазиатский математик 9 в. аль) и др.
Решения практической задачи в 30-х годах XX века в Великобритании при создании системы противовоздушной обороны.
Конец 40-х — начало 50-х годов XX века – появление ЭВМ и ракетно-ядерная программа.
Конец XX — начало XXI веков – появление высокоэффективных методов моделирования, рассчитанных на современные компьютеры.

Применения математического моделирования в различных областях
энергетика: управление ядерными реакторами, моделирование термоядерных процессов, прогнозирование энергетических процессов, управление энергоресурсами;
космонавтика: расчет траекторий и управления полетом космических аппаратов, моделирование конструкций летательных аппаратов, обработка спутниковой информации;
медицина: моделирование, прогнозирование эпидемий, инфекционных процессов, управление процессом лечения, диагностика болезней;
производство: управление техническими и технологическими процессами и системами, ресурсами (запасами), планирование, прогнозирование оптимальных процессов производства;
экология: моделирование загрязнения экологических систем, прогноз причинно-следственных связей в экологической системе, откликов системы на те или иные воздействия экологических факторов.
1б. Математическое моделирование

Аналитическая модель исследуется следующими методами:
аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик системы;
численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты, но при конкретных начальных данных;
качественным, когда не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
2а. Аналитическое моделирование

2а. Аналитическое моделирование
Аналитическая модель представляет собой уравнение процесса или систему уравнений.
Пример 1.
Модель, описывающая путь, пройденный автомобилем при равноускоренном движении с момента начала движения:
где v0 и а – начальная скорость и ускорение.
Для того, чтобы вычислить значение пути S(t) в заданный момент времени t = τ достаточно подставить конкретные значения и выполнить расчет при t = τ.

Пример 2.
Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением:
где m и l – масса и длина подвеса маятника; g – ускорение свободного падения; φ(t) – угол отклонения маятника в момент времени t.
Из этого уравнения можно найти точные значения интересующих характеристик с помощью методов решения дифференциальных уравнений.
где А и ε – постоянные, зависящие от начальных условий.
2а. Аналитическое моделирование

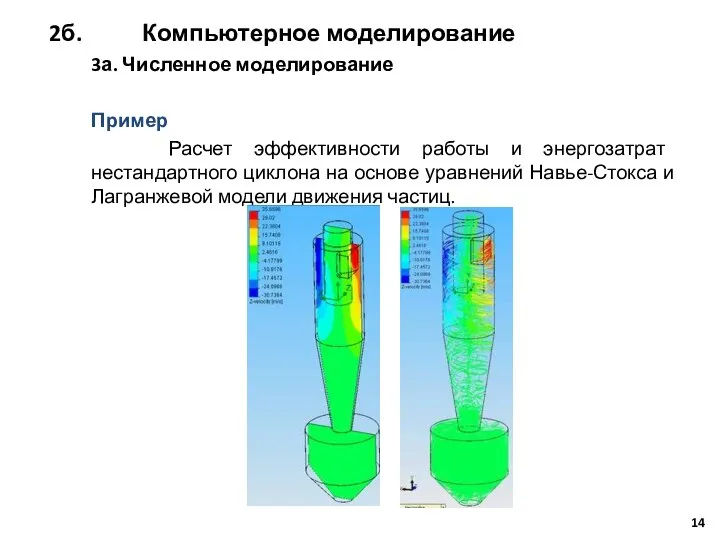
3а. Численное моделирование
Пример
Расчет эффективности работы и энергозатрат нестандартного циклона на основе уравнений Навье-Стокса и Лагранжевой модели движения частиц.
2б. Компьютерное моделирование

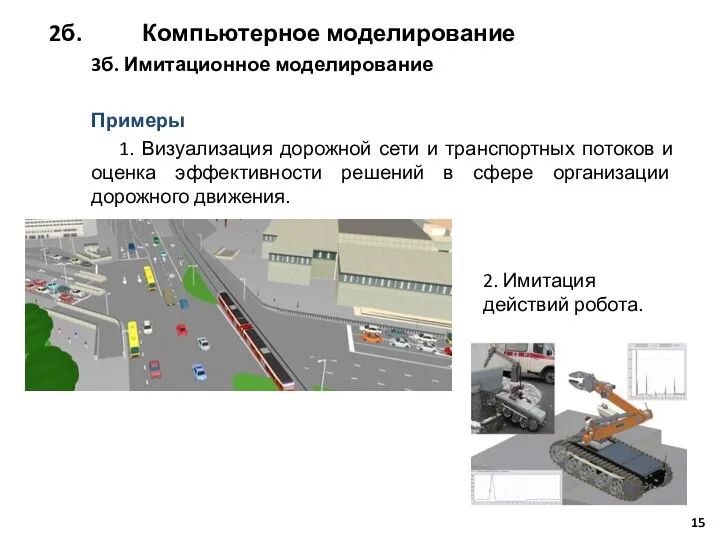
2. Имитация действий робота.
3б. Имитационное моделирование
Примеры
1. Визуализация дорожной сети и транспортных потоков и оценка эффективности решений в сфере организации дорожного движения.
2б. Компьютерное моделирование

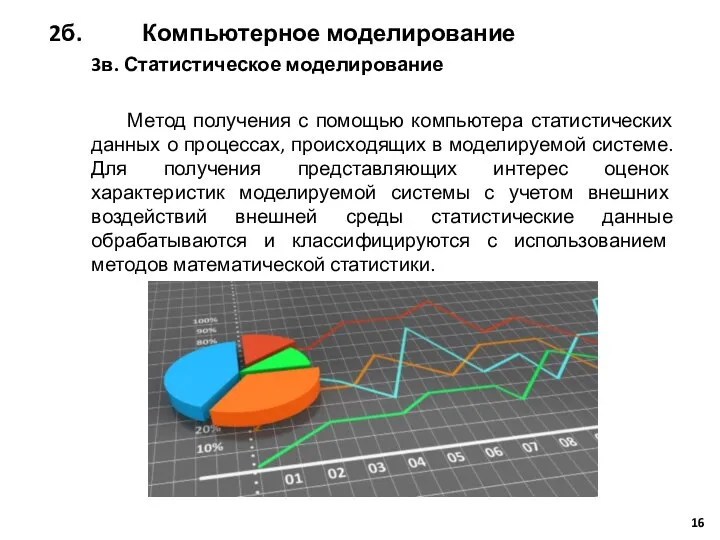
3в. Статистическое моделирование
Метод получения с помощью компьютера статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес оценок характеристик моделируемой системы с учетом внешних воздействий внешней среды статистические данные обрабатываются и классифицируются с использованием методов математической статистики.
2б. Компьютерное моделирование

Вычислительный эксперимент
Вычислительный эксперимент (ВЭ) - метод исследования явления, процесса или машины, для которых разработана компьютерная модель.
Сущность этой методологии состоит в замене исходного объекта его математической моделью и исследовании современными вычислительными средствами математических моделей.
Типы вычислительного эксперимента:
поисковый вычислительный эксперимент
оптимизационный вычислительный эксперимент
диагностический вычислительный эксперимент
вычислительный эксперимент в ситуациях, когда имеется большой разрыв между возможностями теории и эксперимента

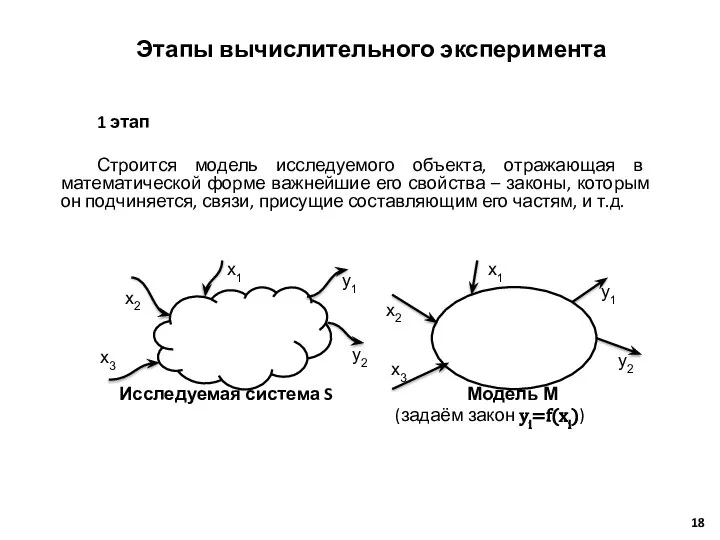
Этапы вычислительного эксперимента
1 этап
Строится модель исследуемого объекта, отражающая в математической форме важнейшие его свойства – законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д.
Исследуемая система S Модель М
(задаём закон yi=f(xi))
x3
x2
x1
y2
y1
x3
x2
x1
y1
y2

2 этап
Выбор или разработка вычислительного алгоритма для реализации модели на компьютере.
Вычислительный алгоритм - точное предписание действий над входными данными, задающее вычислительный процесс, направленный на преобразование произвольных входных данных в полностью определенный этими данными результат.
Необходимо получить искомые величины с заданной точностью на имеющейся вычислительной технике. Вычислительные алгоритмы должны не искажать основные свойства модели, они должны быть адаптирующимися к особенностям решаемых задач и используемых вычислительных средств. Т. е. алгоритм должен быть корректным.
Этапы вычислительного эксперимента

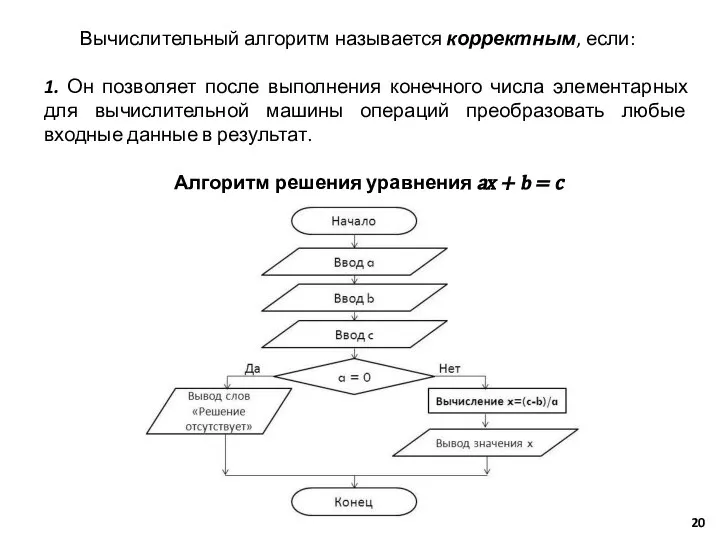
Вычислительный алгоритм называется корректным, если:
1. Он позволяет после выполнения конечного числа элементарных для вычислительной машины операций преобразовать любые входные данные в результат.
Алгоритм решения уравнения ax + b = c

2. Результат устойчив по отношению к малым возмущениям входных данных.
Пусть дана система двух линейных уравнений:
u +10 v = 11,
100u + 1001v = 1101.
Её решением является пара чисел (1; 1).
«Возмутим» правую часть первого уравнения на 0.01.
u +10 v = 11.01,
100u + 1001v = 1101.
Получим новую, «возмущённую» систему, решением которой является пара чисел (11.01; 0,00), не имеющая ничего общего с решением невозмущённой системы.
Изменение значения одного параметра на 0.01 привело к совсем другому решению. Задача является вычислительно неустойчивой.

3 этап
Создание программного обеспечения для реализации модели и алгоритма на компьютере.
Программный продукт должен учитывать важнейшую специфику математического моделирования, связанную с использованием ряда математических моделей, многовариантностью расчетов. Это подразумевает широкое использование комплексов и пакетов прикладных программ, разрабатываемых, в частности, на основе объектно-ориентированного программирования.
Этапы вычислительного эксперимента

4 этап
Проведение расчетов на компьютере.
Результат получается в виде некоторой цифровой информации, которую далее необходимо будет расшифровать.
Точность информации при вычислительном эксперименте определяется:
достоверностью модели, положенной в основу эксперимента;
правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания);
техническими характеристиками вычислительных устройств, на которых выполняются расчеты.
Этапы вычислительного эксперимента

5 этап
Обработка результатов расчетов, их анализ, сопоставление с экспериментальными данными и выводы.
На этом этапе могут возникнуть необходимость уточнения математической модели (усложнения или, наоборот, упрощения), предложения по созданию упрощенных инженерных способов решения и формул, дающих возможности получить необходимую информацию более простым способом.
Этапы вычислительного эксперимента

Области применения вычислительного эксперимента
Фундаментальные науки: механика, физика, астрофизика и др., для которых отмечается наивысший уровень математизации.
Техника и промышленность, технология с целью оптимизации производственных процессов.
Исследование моделей экологически опасных объектов с целью выработки практических рекомендаций по обеспечению условий безопасности функционирования работающих установок и проектируемых объектов.
Медицина и т.д.

Математическая модель – приближенное описание реального процесса, выраженное с помощью математических соотношений.
Любая математическая модель описывает реальный процесс лишь с некоторой степенью приближения к действительности.
Математические модели могут представлять собой системы дифференциальных уравнений (обыкновенных или в частных производных), системы алгебраических уравнений, матричные уравнения, линейные, нелинейные уравнения и т.д.
Математическая модель

Основные требования к математическим моделям
адекватность (соответствие модели своему оригиналу);
объективность (соответствие научных выводов реальным условиям);
простота (не засоренность модели второстепенными факторами);
чувствительность (способность модели реагировать изменению начальных параметров);
устойчивость (малому возмущению исходных параметров должно соответствовать малое изменение решения задачи);
универсальность (широта области применения).

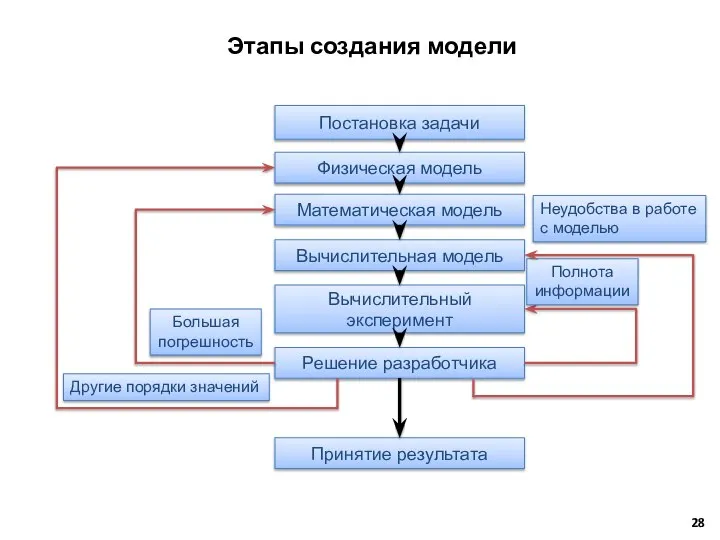
Этапы создания модели
Постановка задачи
Физическая модель
Математическая модель
Вычислительная модель
Вычислительный эксперимент
Решение разработчика
Принятие результата
Большая
погрешность
Другие порядки значений
Полнота
информации
Неудобства в работе
с моделью

Инструменты компьютерного инженерного анализа
CAE-инструменты (Computer Aids Engineering) –
инструменты автоматического инженерного анализа.
CAE-инструменты предназначены для:
оптимизации разработок на начальных этапах проектирования;
снижения стоимости выпускаемой продукции;
сокращения цикла разработки нового изделия;
минимизации количества натурных испытаний;
научных исследований с возможностью свободного управления параметрами, произвольного их изменения, вплоть до придания им нереальных, неправдоподобных значений;
проведения вычислительного эксперимента там, где натурный эксперимент невозможен из-за удаленности исследуемого явления в пространстве либо из-за его значительной растянутости во времени, либо из-за возможности внесения необратимых изменений в изучаемый процесс.

ANSYS – программный продукт, являющийся широко известным CAE-инструментом, появившийся более 30 лет назад, развивающийся и усовершенствующийся и по сей день.
Это передовой комплекс средств компьютерного инженерного моделирования, использующий в своей основе метод конечных элементов.
Инструменты ANSYS позволяют решать всевозможные задачи из различных областей науки: конструкционные, тепловые, гидрогазодинамические, электромагнитные, акустические, междисциплинарные.

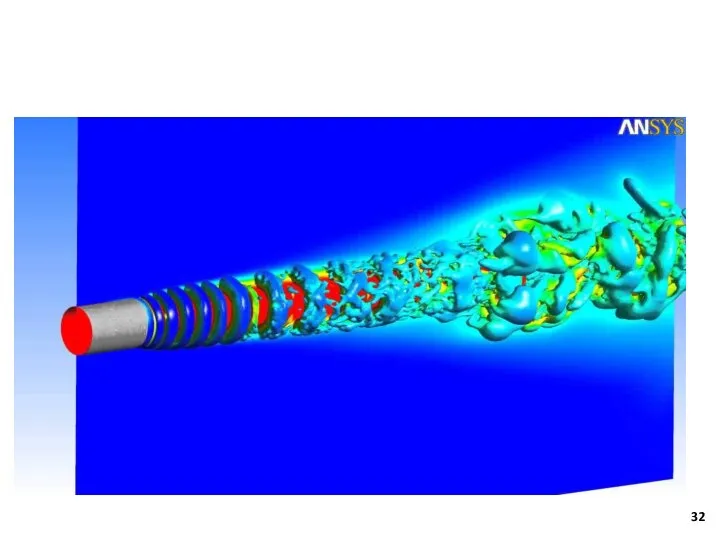
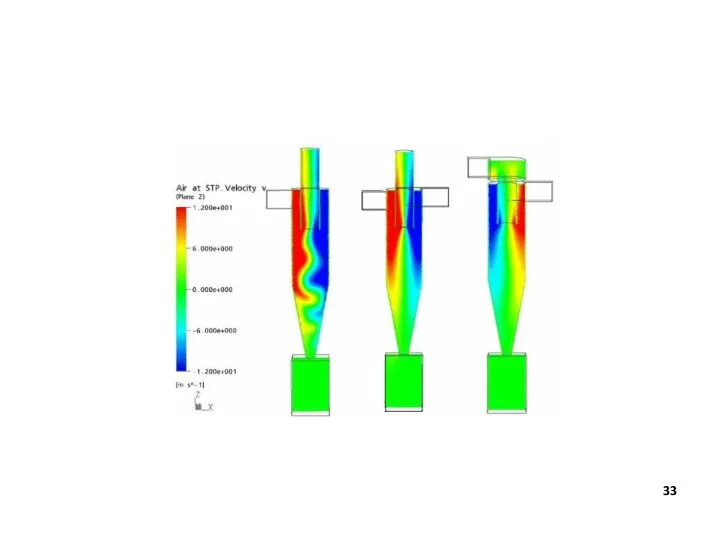
Основные возможности ANSYS
вычислительная гидродинамика

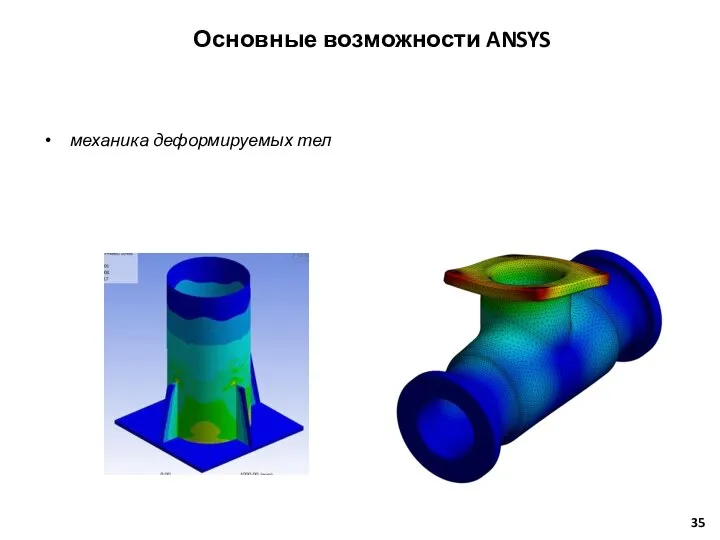
механика деформируемых тел
Основные возможности ANSYS

Электромагнетизм
Основные возможности ANSYS

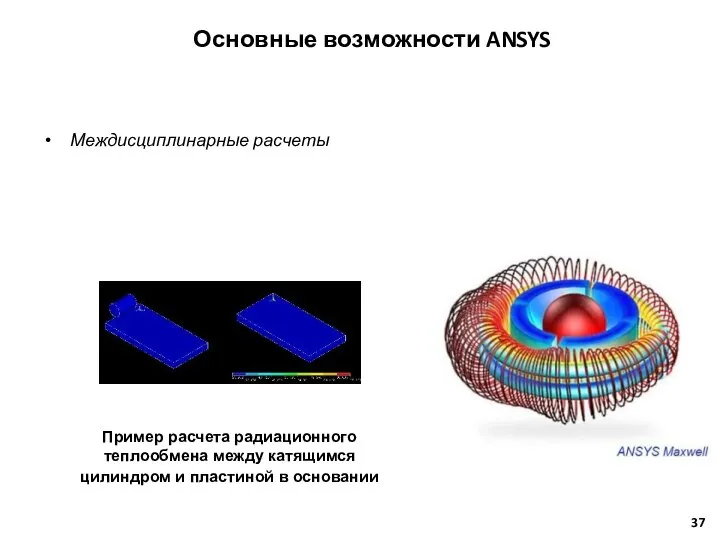
Междисциплинарные расчеты
Пример расчета радиационного теплообмена между катящимся цилиндром и пластиной в основании
Основные возможности ANSYS

Этапы моделирования гидродинамических процессов на базе ANSYS WORKBENCH в приложении ANSYS CFX 1 этап. Подготовка геометрии для численных расчетов
1. Выделение проточной части модели для исследования
Пакеты численного моделирования используются для прогнозирования рабочего процесса механизма или детали. В гидродинамике нас интересуют исключительно гидродинамические характеристики изделий, следовательно, только то место, где течет жидкость (или газ).
Проточная часть – это область изделия, гидродинамические характеристики которой необходимо проверить или изучить.
ANSYS CFX работает исключительно с геометрией проточной части и всякую твердую модель считает объемом жидкости.

Отрезок трубы (колено) Проточная часть трубы
Рабочее колесо насоса Проточная часть колеса
Пример: необходимо изучить течение жидкости/газа в колене трубопровода.
!!! Не нужно рисовать саму трубу, показывать сварные швы, крепеж и пр. Достаточно построить геометрию проточной части.

2. Инструменты для создания геометрических моделей
Простые конфигурации удобнее всего создавать в различных внешних CAD-системах:
КОМПАС
3D
Solid Works
Solid Edge
CATIA
пр.
Для формирования проточных частей межлопастных каналов в динамических машинах (турбины, насосы, вентиляторы) рекомендуется применять специализированные программные модули ANSYS CFX:
Design Modeler
BladeGen

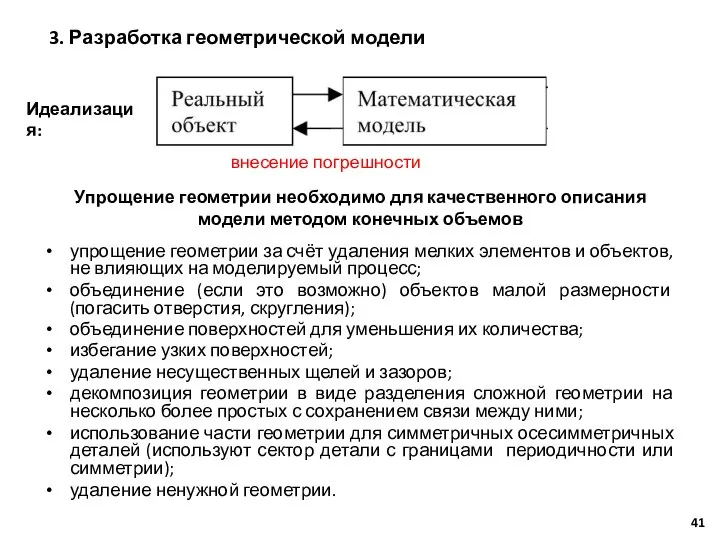
упрощение геометрии за счёт удаления мелких элементов и объектов, не влияющих на моделируемый процесс;
объединение (если это возможно) объектов малой размерности (погасить отверстия, скругления);
объединение поверхностей для уменьшения их количества;
избегание узких поверхностей;
удаление несущественных щелей и зазоров;
декомпозиция геометрии в виде разделения сложной геометрии на несколько более простых с сохранением связи между ними;
использование части геометрии для симметричных осесимметричных деталей (используют сектор детали с границами периодичности или симметрии);
удаление ненужной геометрии.
Идеализация:
внесение погрешности
Упрощение геометрии необходимо для качественного описания
модели методом конечных объемов
3. Разработка геометрической модели

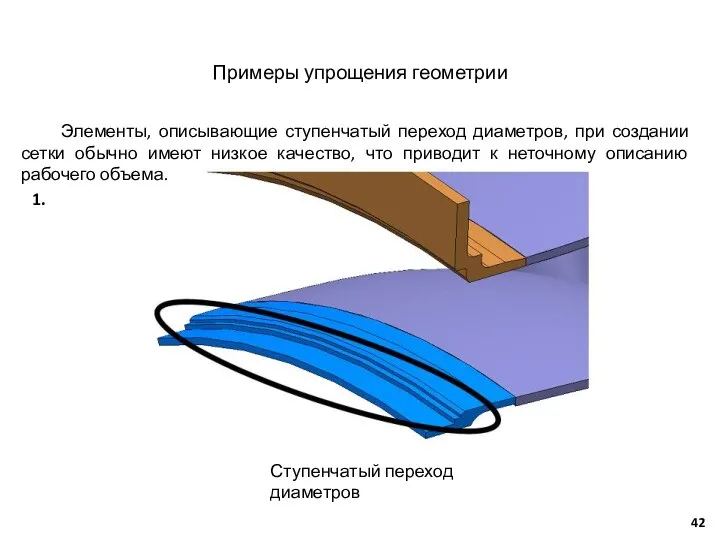
Ступенчатый переход диаметров
Элементы, описывающие ступенчатый переход диаметров, при создании сетки обычно имеют низкое качество, что приводит к неточному описанию рабочего объема.
Примеры упрощения геометрии
1.

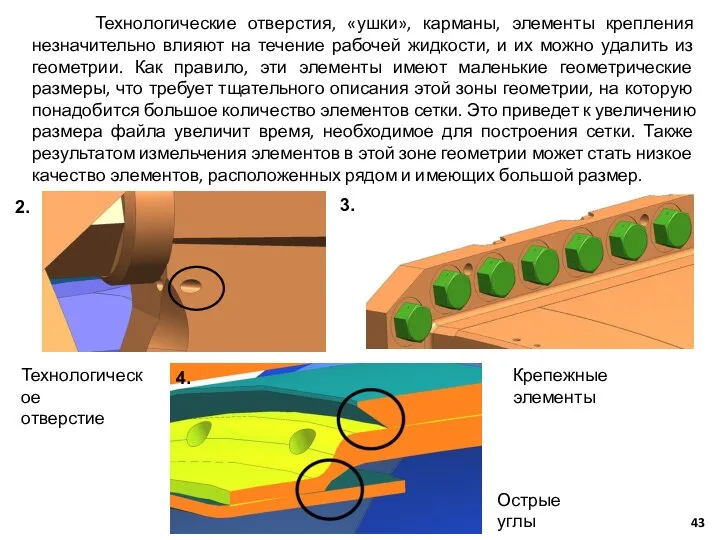
Технологические отверстия, «ушки», карманы, элементы крепления незначительно влияют на течение рабочей жидкости, и их можно удалить из геометрии. Как правило, эти элементы имеют маленькие геометрические размеры, что требует тщательного описания этой зоны геометрии, на которую понадобится большое количество элементов сетки. Это приведет к увеличению размера файла увеличит время, необходимое для построения сетки. Также результатом измельчения элементов в этой зоне геометрии может стать низкое качество элементов, расположенных рядом и имеющих большой размер.
Технологическое
отверстие
Крепежные элементы
Острые углы
2.
3.
4.