Линейные уравнения

Электронный учебник
Составила: учитель математики-информатики
Терегулова И.В.
МОУ «СОШ №1»
2008 год

Дорогой друг!
Твоему вниманию представлен электронный учебник, где ты можешь найти необходимые сведенья для решения линейных уравнений. Освоив способы решения, ты можешь проверить свои знания, решив тестовые задания и самостоятельную работу, после чего компьютер поставит тебе оценку.
Желаю удачи!

Равенство между двумя алгебраическими выражениями с одной переменной называют уравнением с одной неизвестной.
Корнем уравнения называют значение переменной , при котором уравнение обращается в верное числовое равенство.
Решить уравнение означает найти все его корни или доказать, что корней нет.
Уравнения, которые имеют одни и те же корни, называются равносильными.
Уравнения, которые не имеют корней, также считаются равносильными.
Основные понятия:

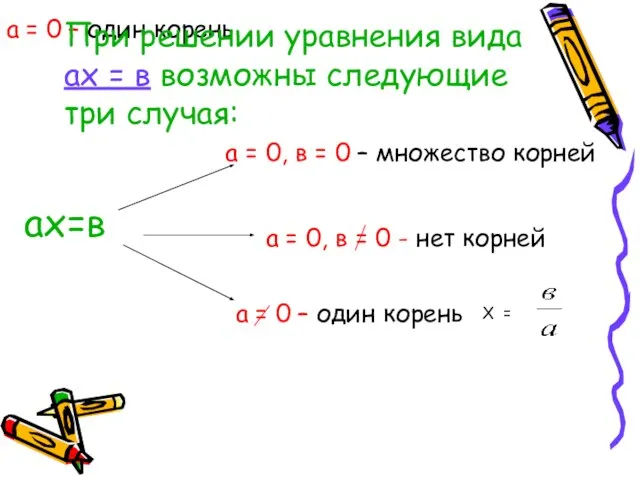
Определение: уравнение вида а х = в (где х – переменная, а и в – некоторые числа) называется линейным уравнением с одной переменной.
Отличительная особенность такого уравнения – переменная х входит в уравнение обязательно в первой степени.

Пример 1
Перечисленные уравнения являются линейными, так как имеют вид а х = в:
а) 3 х=7 (где а=3, в=7);
б) -2 х=5 (где а=?, в=?);
в) 0х=-3 (где а=?, в=?);
г)0х=0 (где а=?, в=?).
Все линейные уравнения приводятся к виду а х = в с помощью тождественных преобразований.

Пример 2
В уравнении 2(3х-5)=х-3 переменная х входит в первой степени. Поэтому это уравнение является линейным. Приведём это уравнение к стандартному виду. В левой части раскроем скобки: 2 3х-2 5=х-3 или 6х-10=х-3.
Перенесём слагаемые, содержащие х, в левую часть уравнения; числа – в правую. Приведём подобные слагаемые. Получаем: 6х-х=10-3 или 5х=7. Линейное уравнение имеет вид ах=в (где а=5, в=7)

При решении уравнений не забудь следующие свойства:
если в уравнении перенести слагаемые из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение равносильное данному.

Пример 3
Перечисленные уравнения не являются линейными:
3х2+6х+7=0 (так как содержит переменную х во второй степени);
2х2-5х3= 3 (объясни сам)
х(х-3)=х5 (объясни сам)

а = 0 – один корень
ах=в
а = 0 – один корень
а = 0, в = 0 - нет корней
а = 0, в = 0 – множество корней
При решении уравнения вида ах = в возможны следующие три случая:
Х =

Пример 4
Решим уравнение 2 (3 х-1)=4 (х +3). Приведём это уравнение к стандартному виду. Раскроем скобки в обеих частях уравнения:2 3 х-2 1=4 х + 4 3 или
6 х - 2= 4 х + 12. Слагаемые, зависящие от х, перенесём в левую часть уравнения; числа – в правую, изменяя их знаки на противоположные:
6 х - 4х = 2+ 12. Приведём подобные слагаемые:
2х = 14 . В этом уравнении а=2 и в=14 . Уравнение имеет один корень х =
=7

Пример 5
Решим уравнение 2( 3 х-1)=4 ( х+3)- 14 +2х. Приводим это уравнение к стандартному виду: 6 х -2= 4 х + 12 – 14 + 2 х или
6 х - 4 х - 2х=2 + 12-14, или 0х=0 (где а=0, в=0 ) .
Очевидно, что при подстановке любого значения х получаем верное числовое равенство 0=0.
Поэтому любое число является корнем этого уравнения (уравнение имеет бесконечно много корней).

Пример 6
Решим уравнение 2 (3 х-1)=4 ( х + 3)+2х
Приводим это уравнение к стандартному виду:
6 х - 2= 4 х+ 12+ 2 х или 6 х - 4 х-2 х= 2+12 или 0х=14 (где а=0, в=14 ).
Очевидно, что при подстановке любого значения х получаем неверное числовое равенство 0=14.
Поэтому уравнение корней не имеет.

Реши сам!
а)5х-7=-2
Ответ:х=?;
б) 2(3х-1)+4=7х+5
Ответ:х=?
в)3х-(10+5х)=54
Ответ:х=?
г) 0,5(4-2х)=х-1,8
Ответ:х=?

а)5x=-2+7
5x=5
х=1 Ответ:х=1
б) 6х-2+4=7х+5
6х-7х=5+2-4
-х=3
х=-3 Ответ:х=-3
в)3х-10-5х=54 -2х=54+10
-2х=64
х=64:(-2)
х=-32 Ответ:х=-32
г) 2-х=х-1,8
-х-х=-1,8-2
-2х=-3,8
х=1,9 Ответ: х=1,9

Тестовая работа
Проверь свои знания ответив на вопросы предложенные компьютером.

Самостоятельная работа
Реши уравнения и компьютер оценит твою работу.

Не расстраивайся, если компьютер тебя не оценил. Вернись к слайду №4, попробуй начать всё сначала и у тебя обязательно всё получится!

1. Реши уравнение: |3х + 8|=1
2. Найди значение параметра а,
при котором уравнение (3а + 1) х = 2а+6
имеет корень х=2
Если ты прошёл тест, решил самостоятельную работу и учитель тебя похвалил, попробуй свои силы при решении следующих уравнений:
1. Реши уравнение: |3х + 8|=1
2. Найди значение параметра а,
при котором уравнение (3а + 1) х = 2а+6
имеет корень х=2
Удачи тебе!