Содержание
- 2. Математика, если на нее правильно посмотреть, отражает не только истину, но и несравненную красоту. Бертранд Рассел.
- 3. Фракталы – это … Нравится ли вам смотреть на ночные молнии или представлять синии всполохи ветвящихся
- 4. История фракталов История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого
- 5. Отец фракталов Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо
- 6. Немного о размерностях В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы прикидываем длину дороги
- 7. Фракталы делятся на группы. Самые большие группы это: Геометрические фракталы Алгебраические фракталы Системы итерируемых функций Стохастические
- 8. Геометрические фракталы. Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических
- 9. Алгебраические фракталы Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их
- 10. Алгебраические фракталы На всякий случай напомню, что такое комплексные числа. Комплексное число - это число, состоящее
- 11. Стохастические фракталы Типичный представитель данного класса фракталов "Плазма". Для ее построения возьмем прямоугольник и для каждого
- 12. Стохастические фракталы Если в L-systems (алгебраических фракталах) речь шла о замене прямой линии неким полигоном, то
- 13. Фракталы и хаос Понятие фрактал неразрывно связано с понятием хаос. Хаос - это отсутствие предсказуемости. Хаос
- 14. Вот и подошла к концу наша экскурсия в мир фракталов. Она только немного приоткрыла нам завесу
- 15. Коллекция фракталов:
- 16. Коллекция фракталов:
- 17. Коллекция фракталов:
- 18. Коллекция фракталов:
- 19. Коллекция фракталов:
- 20. Коллекция фракталов:
- 21. Коллекция фракталов:
- 22. Коллекция фракталов:
- 23. Коллекция фракталов:
- 24. Коллекция фракталов:
- 25. Коллекция фракталов:
- 26. Коллекция фракталов:
- 28. Скачать презентацию
Слайд 2Математика, если на нее правильно
посмотреть, отражает не только истину,
но и несравненную красоту.
Бертранд
Математика, если на нее правильно
посмотреть, отражает не только истину,
но и несравненную красоту.
Бертранд

Слайд 3Фракталы – это …
Нравится ли вам смотреть на ночные молнии или представлять
Фракталы – это …
Нравится ли вам смотреть на ночные молнии или представлять

Фракталами называют бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба. Разветвления трубочек трахей, нейроны, сосудистая система человека, извилины берегов морей и озер, контуры деревьев — это все фракталы. Фракталы находят в местах таких малых, как клеточная мембрана, и таких огромных, как звездные галактики. Можно сказать, что фракталы – это уникальные объекты, порожденные непредсказуемыми движениями хаотического мира!
Слайд 4История фракталов
История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX
История фракталов
История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX

Слайд 5Отец фракталов
Вплоть до 20 века шло накопление данных о таких странных
Отец фракталов
Вплоть до 20 века шло накопление данных о таких странных

Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).
Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта "The Fractal Geometry of Nature" ("Фрактальная геометрия природы") ставший классическим - "Какова длина берега Британии?". Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра - мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно - длина берега Британии бесконечна.
Слайд 6Немного о размерностях
В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы
Немного о размерностях
В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы

Размерность 2 означает, что любую точку мы можем однозначно определить двумя числами. Не надо думать, что двумерный - значит плоский. Поверхность сферы тоже двумерна (ее можно определить с помощью двух значений - углов наподобие ширины и долготы).
Если смотреть с математической точки зрения, то размерность определяется следующим образом: для одномерных объектов - увеличение в два раза их линейного размера приводит к увеличению размеров (в данном случае длинны) в два раза (2^1).
Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (например, площадь прямоугольника) в четыре раза (2^2).
Для 3-х мерных объектов увеличение линейных размеров в два раза приводи к увеличению объема в восемь раз (2^3) и так далее.
Таким образом, размерность D можно рассчитать исходя из зависимости увеличения "размера" объекта S от увеличения линейных размеров L. D=log(S)/log(L). Для линии D=log(2)/log(2)=1. Для плоскости D=log(4)/log(2)=2. Для объема D=log(8)/log(2)=3. Может быть немного запутано, но в общем-то несложно и понятно.
Зачем я это все рассказываю? А для того чтобы понять, как отделять фракталы от, скажем, колбасы. Попробуем посчитать размерность для кривой Пеано. Итак, у нас исходная линия, состоящая из трех отрезков длинны Х, заменяется на 9 отрезков втрое меньшей длинны. Таким образом, при увеличении минимального отрезка в 3 раза длина всей линии увеличивается в 9 раз и D=log(9)/log(3)=2 - двумерный объект!!!
Фрактал это ...
Так вот, когда размерность фигуры получаемой из каких-то простейших объектов (отрезков) больше размерности этих объектов - мы имеем дело с фракталом.
Слайд 7
Фракталы делятся на группы. Самые большие группы это:
Геометрические фракталы
Алгебраические фракталы
Фракталы делятся на группы. Самые большие группы это:
Геометрические фракталы
Алгебраические фракталы

Системы итерируемых функций
Стохастические фракталы
Слайд 8Геометрические фракталы.
Именно с них и начиналась история фракталов. Этот тип фракталов получается
Геометрические фракталы.
Именно с них и начиналась история фракталов. Этот тип фракталов получается

Из этих геометрических фракталов очень интересным и довольно знаменитым является первый - снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадь. Попробуйте сделать то же самое методами и фигурами из евклидовой геометрии.
Слайд 9Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили за
Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили за

С течением времени стремится к бесконечности.
Стремится к 0
Принимает несколько фиксированных значений и не выходит за их пределы.
Поведение хаотично, без каких либо тенденций.
Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта.
Для его построения нам необходимы комплексные числа. Любой уважающий себя язык программирования включает в себя инструментарий для работы с комплексными числами, а даже если и нет, то их несложно запрограммировать и самим, и на крайний случай (а таких, я думаю, будет большинство :)) у нас есть Fractint которая все посчитает и нарисует за нас.
Слайд 10Алгебраические фракталы
На всякий случай напомню, что такое комплексные числа. Комплексное число
Алгебраические фракталы
На всякий случай напомню, что такое комплексные числа. Комплексное число

Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень, нельзя только их сравнивать. Комплексное число можно изобразить как точку на плоскости, у которой координата Х это действительная часть a, а Y это коэффициент при мнимой части b.
Функционально множество Мандельброта определяется как Zn+1=Zn*Zn+C. Для построения множества Мандельброта воспользуемся алгоритмом на псевдо Бейсике (легко для понимания и перевода на любимые языки).
For a=-2 to 2 ' для всех действительных а от -2 до 2For b=-2 to 2 ' для всех мнимых b от -2 до 2С=a+biZ0=0+0iLake=True 'Принадлежит множеству МандельбротаFor iteration=1 to 255'Повторяем 255 раз (для режима 256 цветов)Zn=Z0*Z0+CIf abs(Zn)>2 then Lake=False: Exit For 'Проверили - не принадлежитZ0=ZnNextIf Lake=True Then PutPixel(a,b,BLACK) 'Нарисовали черную точку,принадлежащую "озеру" Мандельброта.Else PutPixel(a, b, iteration) ' Нарисовали точку не принадлежащую множеству или лежащую на границе.NextNext
А теперь опишу программку словами. Для всех точек на комплексной плоскости в интервале от -2+2i до 2+2i выполняем некоторое достаточно большое количество раз Zn=Z0*Z0+C, каждый раз проверяя абсолютное значение Zn. Если это значение больше 2, что рисуем точку с цветом равным номеру итерации на котором абсолютное значение превысило 2, иначе рисуем точку черного цвета. Все множество Мандельброта в полной красе у нас перед глазами.
Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное это границы множества. Они то и являются фрактальными. На границах этого множества функция ведет себя непредсказуемо - хаотично.
Меняя функцию, условия выхода из цикла можно получать другие фракталы. Например, взяв вместо выражения С=a+bi выражение Z0=a+bi, а С присваивать произвольные значения мы получим множество Жюлиа, тоже красивый фрактал.
На рисунке, изображающем множество Мандельброта я взял небольшой участок и увеличил его до размеров всего экрана (как в микроскоп). Что же мы видим? Проявление самоподобности. Не точной самоподобности, но близкой и с ней мы будем сталкиваться постоянно, увеличивая части нашего фрактала больше и больше. До каких же пор мы можем увеличивать наше множество? Так вот если мы увеличим его до предела вычислительной мощности компьютеров, то покроем площадь равную площади солнечной системы вплоть до Сатурна.
Слайд 11Стохастические фракталы
Типичный представитель данного класса фракталов "Плазма".
Для ее построения возьмем прямоугольник
Стохастические фракталы
Типичный представитель данного класса фракталов "Плазма".
Для ее построения возьмем прямоугольник

Эта группа фракталов получила широкое распространение благодаря работам Майкла Барнсли из технологического института штата Джорджия. Он пытался кодировать изображения с помощью фракталов. Запатентовав несколько идей по кодированию изображений с помощью фракталов, он основал фирму "Iterated Systems", которая через некоторое время выпустила первый продукт "Images Incorporated", в котором можно было изображения переводить из растровой формы во фрактальную FIF. Это позволяло добиться высоких степеней сжатия. При низких степенях сжатия качество рисунков уступало качеству формата JPEG, но при высоких картинки получались более качественными. В любом случае этот формат не прижился, но работы по его усовершенствованию ведутся до сих пор. Ведь этот формат не зависит от разрешения изображения. Так как изображение закодировано с помощью формул, то его можно увеличить до любых размеров и при этом будут появляться новые детали, а не просто увеличится размер пикселей. Хуже это или лучше - решать надо в каждом отдельном случае.
Слайд 12Стохастические фракталы
Если в L-systems (алгебраических фракталах) речь шла о замене прямой линии
Стохастические фракталы
Если в L-systems (алгебраических фракталах) речь шла о замене прямой линии

В результате можно получить потрясающие коэффициенты сжатия. Например рисунок папоротника кодируется с помощью 28!!! цифр и один и тот же рисунок получается в не зависимости от того что взяли за основу - прямоугольник, круг, треугольник или что-либо еще. Но к сожалению процесс создания набора коэффициентов для произвольного изображения очень трудоемок и занимает очень много времени.
Слайд 13Фракталы и хаос
Понятие фрактал неразрывно связано с понятием хаос. Хаос -
Фракталы и хаос
Понятие фрактал неразрывно связано с понятием хаос. Хаос -

Слайд 14 Вот и подошла к концу наша экскурсия в мир фракталов. Она
Вот и подошла к концу наша экскурсия в мир фракталов. Она

Надеюсь она Вам понравилась.
И на последок хочу поделится с Вами своей коллекцией фракталов.
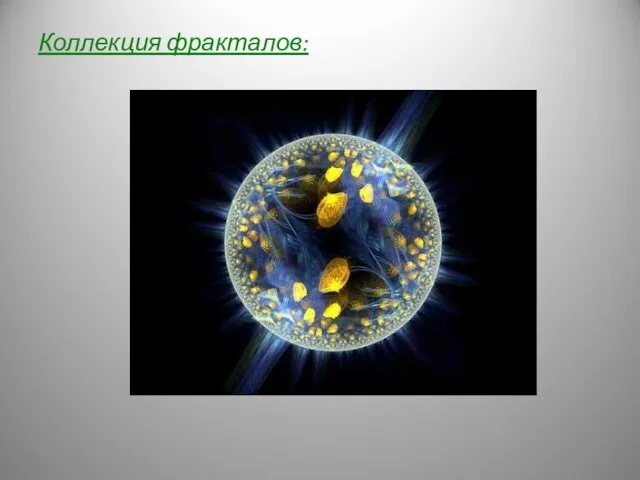
Слайд 15Коллекция фракталов:
Коллекция фракталов:

Слайд 16Коллекция фракталов:
Коллекция фракталов:

Слайд 17Коллекция фракталов:
Коллекция фракталов:
Слайд 18Коллекция фракталов:
Коллекция фракталов:

Слайд 19Коллекция фракталов:
Коллекция фракталов:

Слайд 20Коллекция фракталов:
Коллекция фракталов:

Слайд 21Коллекция фракталов:
Коллекция фракталов:
Слайд 22Коллекция фракталов:
Коллекция фракталов:

Слайд 23Коллекция фракталов:
Коллекция фракталов:
Слайд 24Коллекция фракталов:
Коллекция фракталов:
Слайд 25Коллекция фракталов:
Коллекция фракталов:

Слайд 26Коллекция фракталов:
Коллекция фракталов:
 Презентация на тему Пищеварение в ротовой полости
Презентация на тему Пищеварение в ротовой полости  Межкультурная компетенция
Межкультурная компетенция Миссия бренда
Миссия бренда Виртуальные книжные выставки: особенность технологии создания
Виртуальные книжные выставки: особенность технологии создания Способы образования глаголов
Способы образования глаголов Этапы развития коммерческого права в России
Этапы развития коммерческого права в России Профессиональное определение и его факторы
Профессиональное определение и его факторы Электронный учебникКак понимать и как применять
Электронный учебникКак понимать и как применять Графическое решение физических задач
Графическое решение физических задач ДЗ Урок 1
ДЗ Урок 1 Big Apple International Group
Big Apple International Group Как приготовить манты
Как приготовить манты Диалекты в китайском языке
Диалекты в китайском языке СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ РАЗВИТИЕМ ТЕРРИТОРИАЛЬНОЙ ЕДИНИЦЫБАЙДАКОВ СЕРГЕЙ ЛЬВОВИЧЗАМЕСТИТЕЛЬ МЭРА МОСКВЫ
СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ РАЗВИТИЕМ ТЕРРИТОРИАЛЬНОЙ ЕДИНИЦЫБАЙДАКОВ СЕРГЕЙ ЛЬВОВИЧЗАМЕСТИТЕЛЬ МЭРА МОСКВЫ  Тесты по русскому языку №1
Тесты по русскому языку №1 Зонирование образовательного процесса: - зона двигательной активности - естественно научная зона - географическая зона
Зонирование образовательного процесса: - зона двигательной активности - естественно научная зона - географическая зона Презентация на тему Современные педагогические технологии
Презентация на тему Современные педагогические технологии Познавательные процессы (память)
Познавательные процессы (память) Ремкомплекты суппортов Moniva (страна-производитель Турция)
Ремкомплекты суппортов Moniva (страна-производитель Турция) Конституция - основной закон жизни
Конституция - основной закон жизни Птицы - наши друзья!
Птицы - наши друзья! Культура второй половины XX в
Культура второй половины XX в Требования к фасилитатору
Требования к фасилитатору Закон Российской Федерации о техническом регулировании и европейский подход
Закон Российской Федерации о техническом регулировании и европейский подход Ассорти по-русски
Ассорти по-русски Услышь меня. Мастер-класс
Услышь меня. Мастер-класс Серебряный век Русской литературы
Серебряный век Русской литературы Техническое обслуживанием ремонт трехфазных силовых трансформаторов
Техническое обслуживанием ремонт трехфазных силовых трансформаторов