Линия, прямая в пространстве

Лекция 5
Аналитическая геометрия
1. Аналитическое представление линии и поверхности в пространстве .
2.Плоскость в пространстве.
3. Прямая в пространстве.

Аналитическое представление линии и
поверхности в пространстве.
Задачей аналитической геометрии является изучение геометрических объектов аналитическими методами, то есть средствами алгебры и математического анализа, без геометрических построений.
Геометрические объекты: точка,линия,поверхность, тело.

В основе аналитической геометрии лежит метод координат , позволяющий описывать положение точки в пространстве с помощью чисел (координат точки), что и обеспечивает возможность привлечения методов алгебры и анализа .
Из всех используемых при этом систем координат наиболее часто применяется декартова система – совокупность точки О и ортонормированного базиса
- координатные оси.

Точку М можно задать вектором
Декартовыми координатами точки М называются декартовы координаты её радиус-вектора

Более сложные геометрические объекты задаются
уравнениями (или неравенствами), связывающими
координаты точек, образующих эти объекты.

Линия на плоскости .

Пример.

Поверхность в пространстве .
Пусть
- некоторая поверхность.
Уравнение вида Ф(x,y,z)=0 называется уравнением
этой поверхности,если ему удовлетворяют координаты
любой точки M(x,y,z) лежащей на этой поверхности и
не удовлетворяют координаты ни одной точки, не
лежащей на этой поверхности.

Пример:
Поверхность - геометрическое место точек, координаты которых удовлетворяют уравнению Ф(x,y,z)=0.

Линия в пространстве .
Кривую в пространстве можно рассматривать как линию пересечения двух поверхностей, то есть как геометрическое место точек, принадлежащих обеим поверхностям.

Следовательно, координаты этих точек должны удовлетворять системе уравнений :
(Здесь Ф1(x,y,z)=0 и Ф2(x,y,z)=0 – уравнения пересекающихся поверхностей).

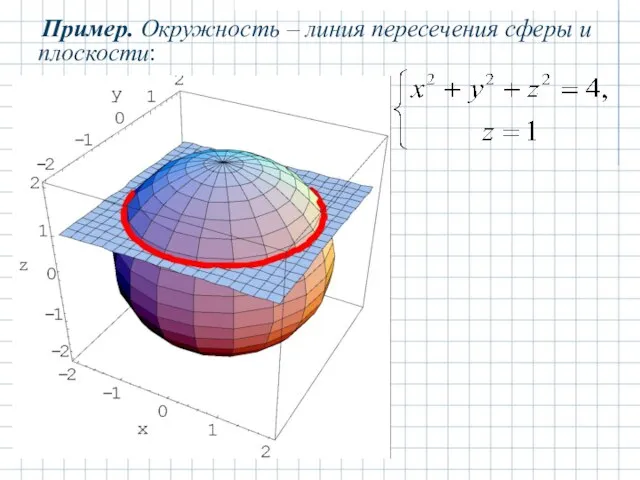
Пример. Окружность – линия пересечения сферы и
плоскости:

Параметрические уравнения линии и поверхности .
При параметрическом задании линии L, её можно
рассматривать как траекторию движения точки
M(x,y,z):
, t – параметр, играющий роль времени.
Уравнения задают положение точки в каждый момент
времени.

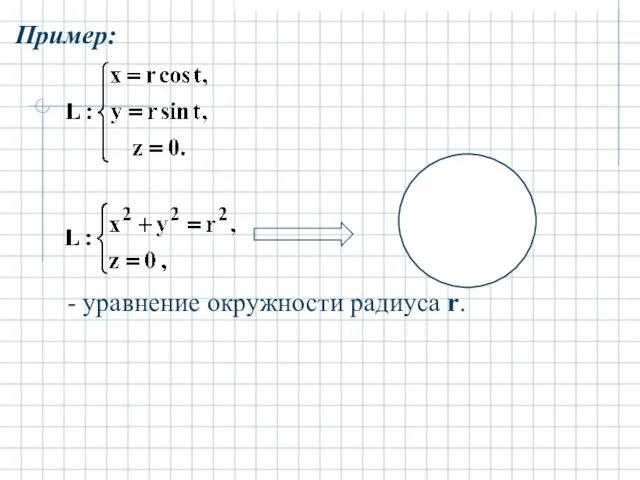
Пример:
- уравнение окружности радиуса r.

Для параметрического задания поверхности S
необходимы два параметра – u и v :

Пример. Уравнение сферы радиуса R:

Плоскость в пространстве.
фиксированная точка плоскости.
произвольная точка плоскости.
- векторное уравнение плоскости.
- нормальный вектор плоскости.

уравнение плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно вектору .
- общее уравнение плоскости.

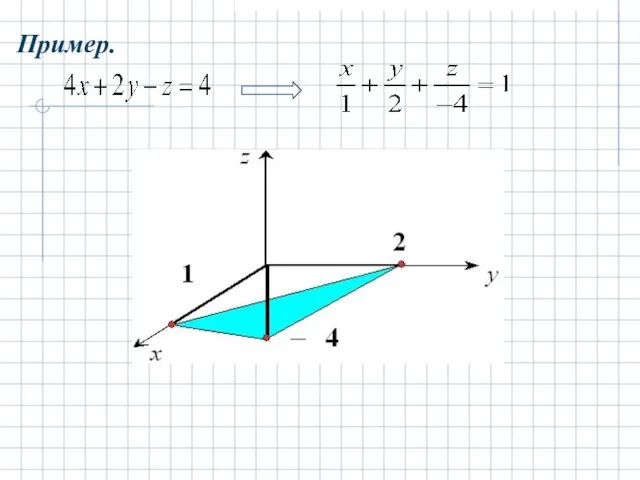
- уравнение плоскости «в отрезках».
Здесь P1(a,0,0), P2(0,b,0), P3(0,0,c) – точки пересечения плоскости с координатными осями,
- «отрезки», отсекаемые плоскостью на координатных осях.

Пример.

Угол между двумя плоскостями .
Рассмотрим

Условие перпендикулярности двух плоскостей.
Условие параллельности двух плоскостей.

Прямая в пространстве.
- произвольная точка прямой

- векторное уравнение прямой.
- канонические уравнения прямой.
- параметрические уравнения прямой.

- общие уравнения прямой.
Эти уравнения определяют прямую как линию пересечения двух не параллельных плоскостей .

Угол между двумя прямыми
Если

Угол между прямой и плоскостью.
Пусть

Условие параллельности двух прямых.
Условие перпендикулярности двух прямых.

Условие параллельности прямой и плоскости.
Условие перпендикулярности прямой и плоскости.

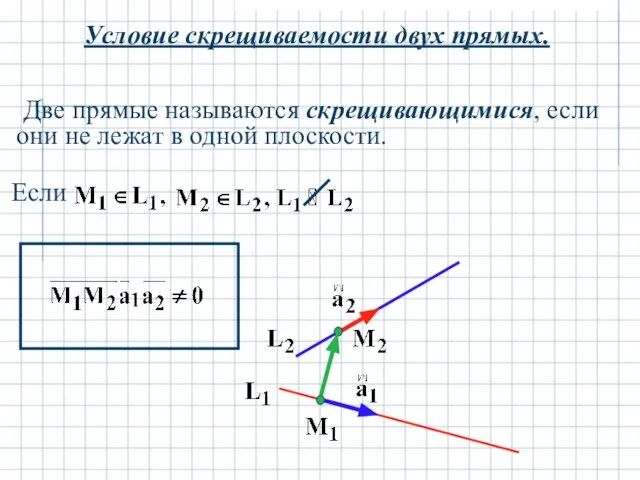
Условие скрещиваемости двух прямых.
Две прямые называются скрещивающимися, если
они не лежат в одной плоскости.
Если

МКТ 7
1. Записать координаты нормального вектора плоскости
2. Какое произведение векторов использовано в условии ортогональности двух плоскостей