Содержание
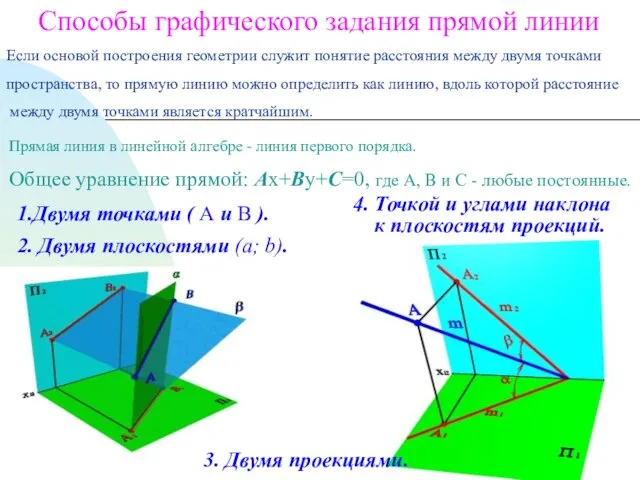
- 2. Способы графического задания прямой линии Если основой построения геометрии служит понятие расстояния между двумя точками пространства,
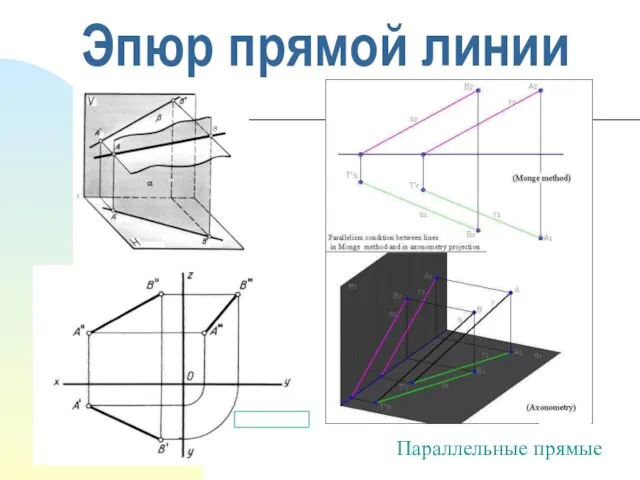
- 3. Эпюр прямой линии Параллельные прямые
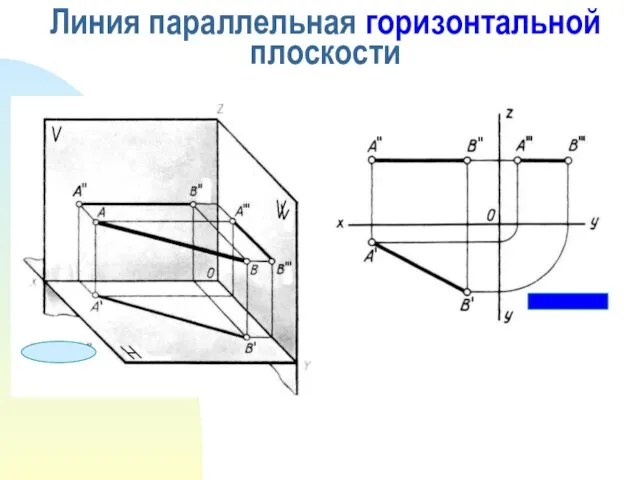
- 4. Линия параллельная горизонтальной плоскости
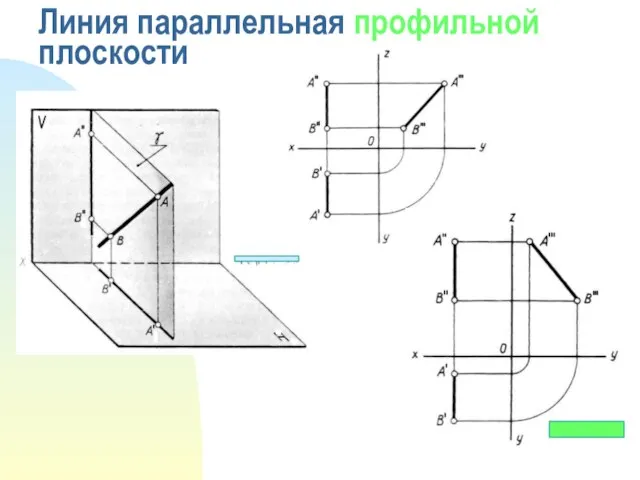
- 5. Линия параллельная профильной плоскости
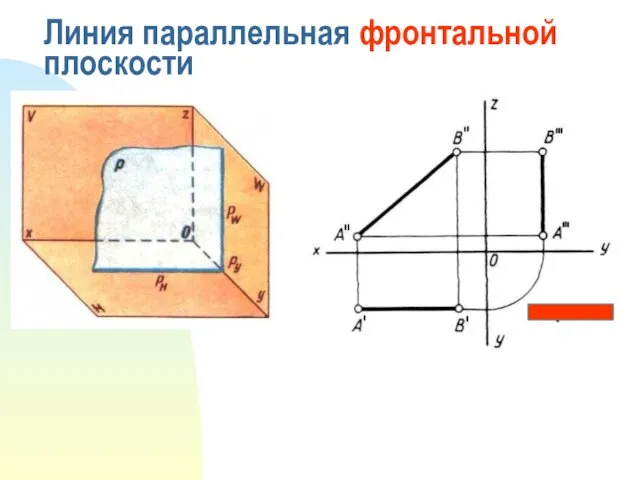
- 6. Линия параллельная фронтальной плоскости
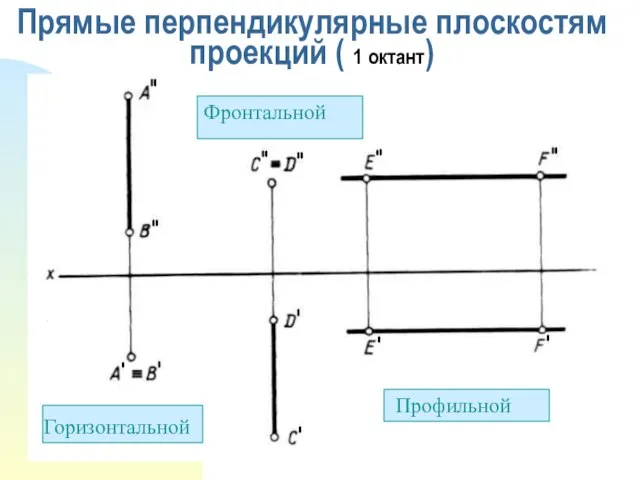
- 7. Прямые перпендикулярные плоскостям проекций ( 1 октант) Профильной ПП Профильной Горизонтальной Фронтальной
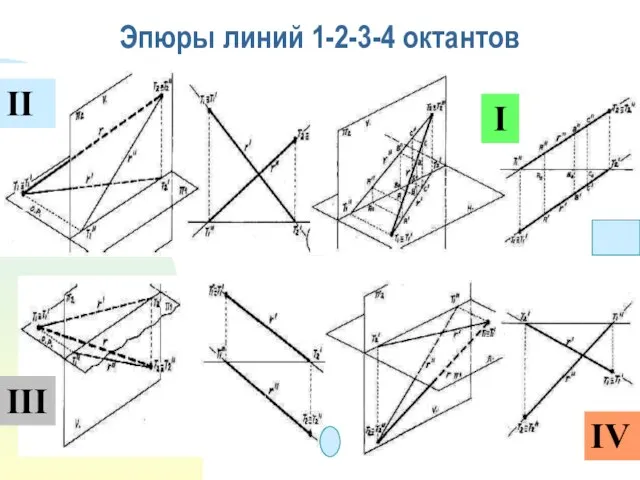
- 8. Эпюры линий 1-2-3-4 октантов I II IV III
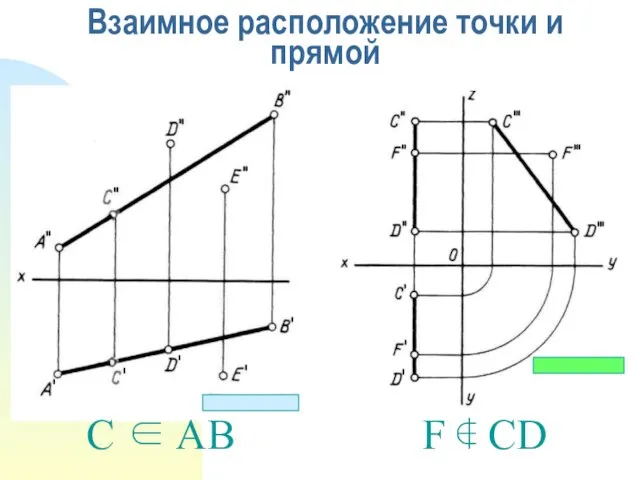
- 9. Взаимное расположение точки и прямой C ∈ AB F ∉ CD
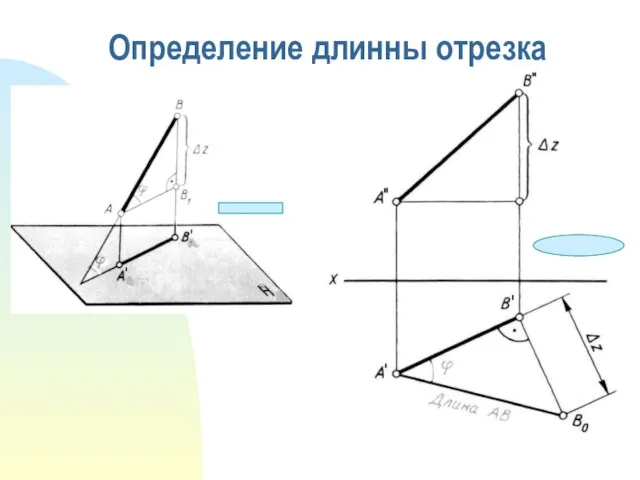
- 10. Определение длинны отрезка
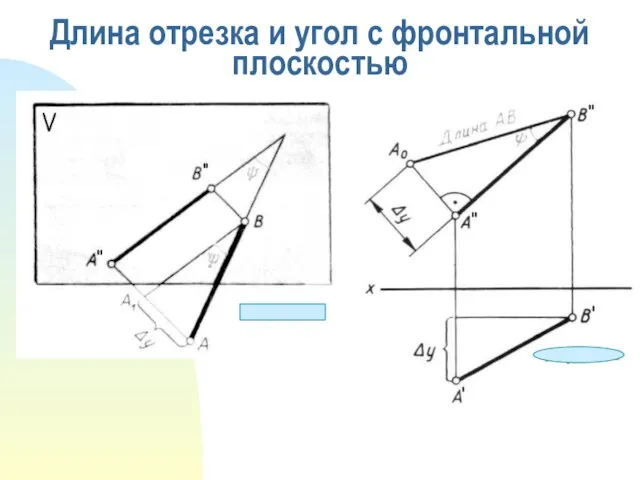
- 11. Длина отрезка и угол с фронтальной плоскостью
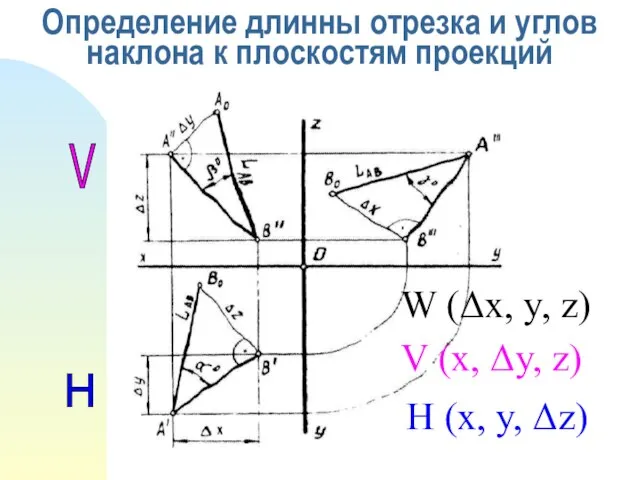
- 12. Определение длинны отрезка и углов наклона к плоскостям проекций W (Δx, y, z) V (x, Δy,
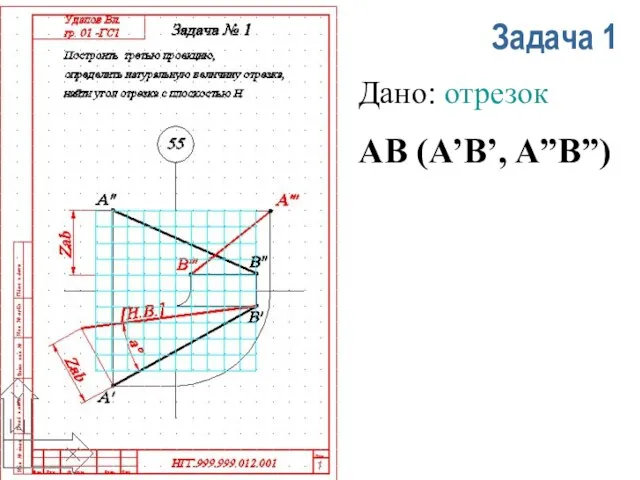
- 13. Задача 1 Дано: отрезок АВ (A’B’, A”B”)
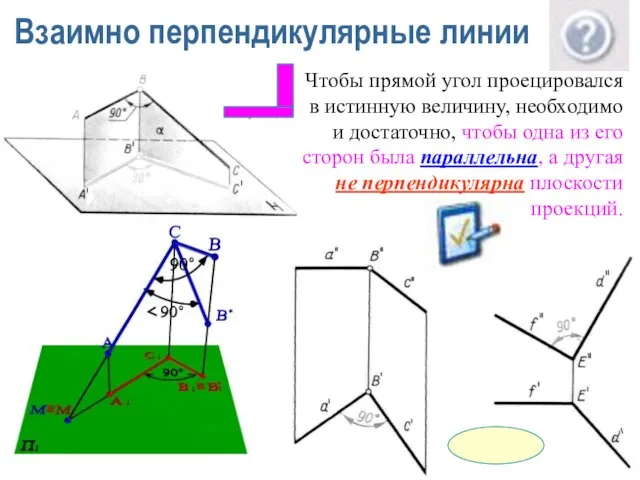
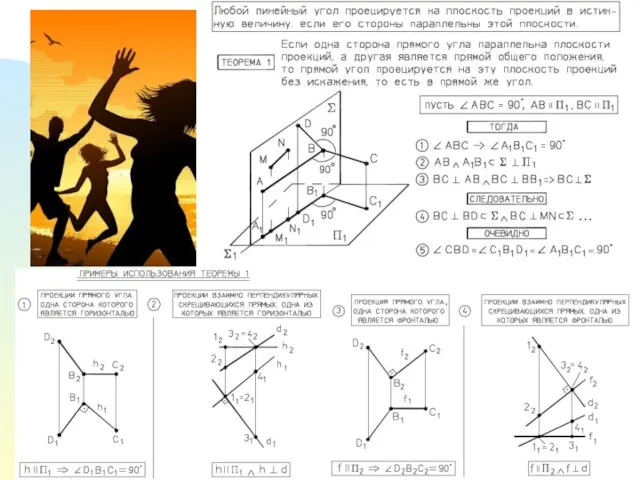
- 14. Взаимно перпендикулярные линии Чтобы прямой угол проецировался в истинную величину, необходимо и достаточно, чтобы одна из
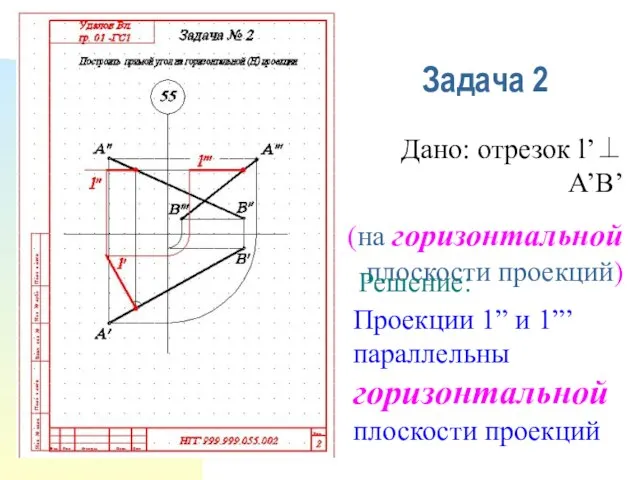
- 15. Задача 2 Дано: отрезок l’⊥ A’B’ (на горизонтальной плоскости проекций) Решение: Проекции 1” и 1”’ параллельны
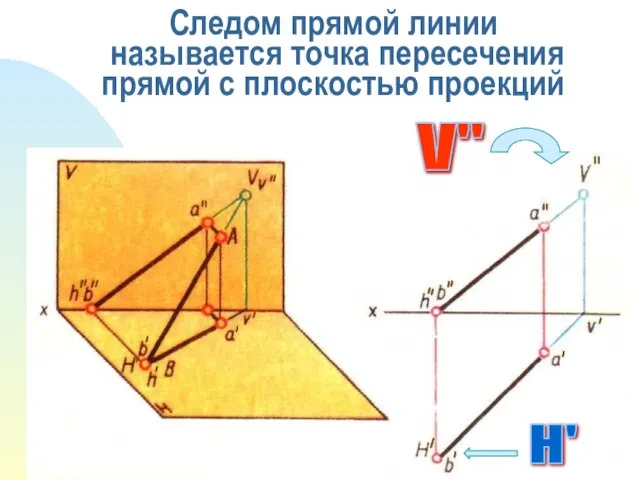
- 17. Следом прямой линии называется точка пересечения прямой с плоскостью проекций H' V"
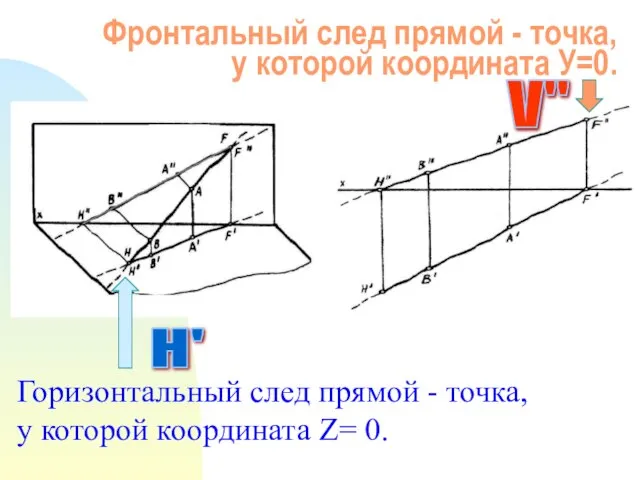
- 18. Фронтальный след прямой - точка, у которой координата У=0. Горизонтальный след прямой - точка, у которой
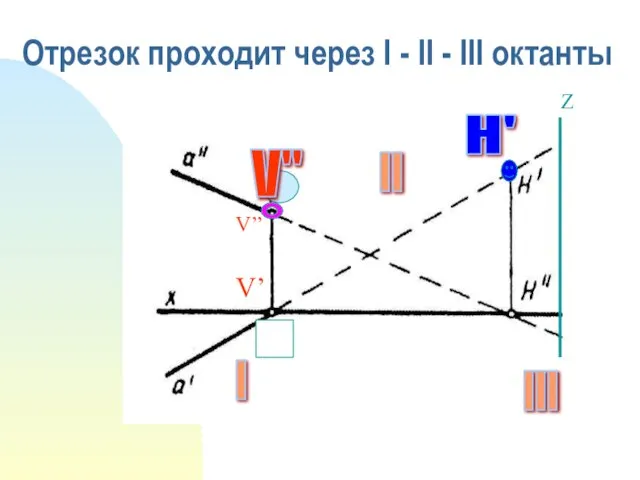
- 19. Отрезок проходит через I - II - III октанты V’ V’’ I II III Z V"
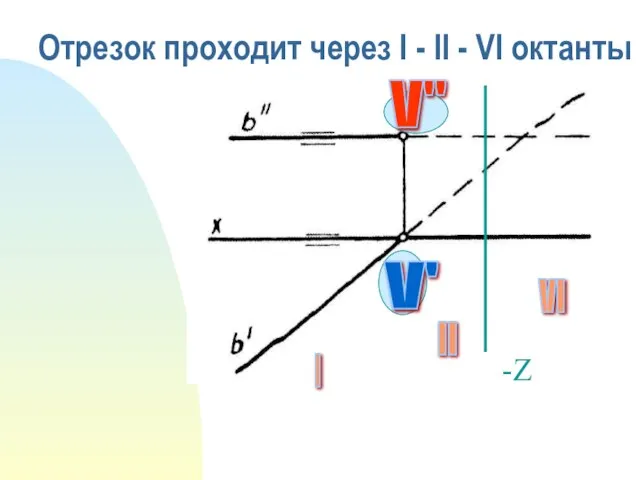
- 20. Отрезок проходит через I - II - VI октанты -Z I II VI V" V'
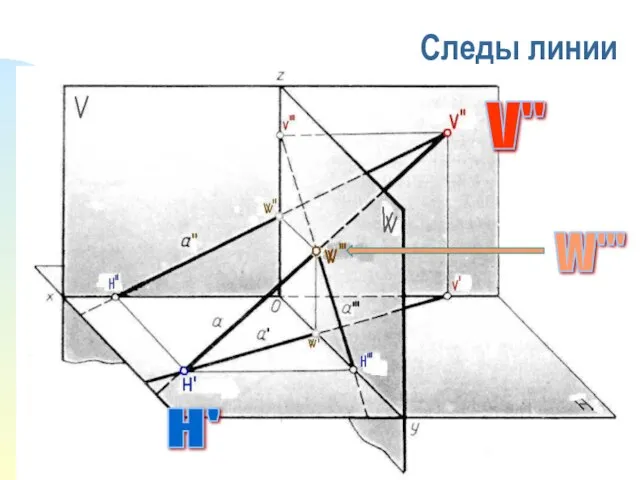
- 21. Следы линии H' V" W'''
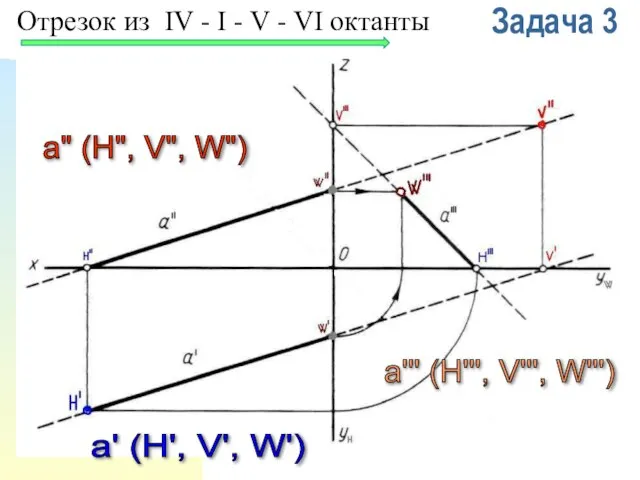
- 22. Задача 3 a" (H", V", W") a' (H', V', W') a''' (H''', V''', W''') Отрезок из
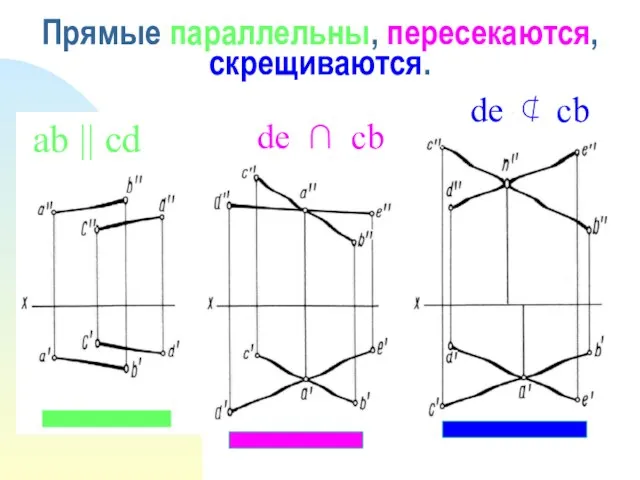
- 23. Прямые параллельны, пересекаются, скрещиваются. ab || cd de ∩ cb de ⊄ cb
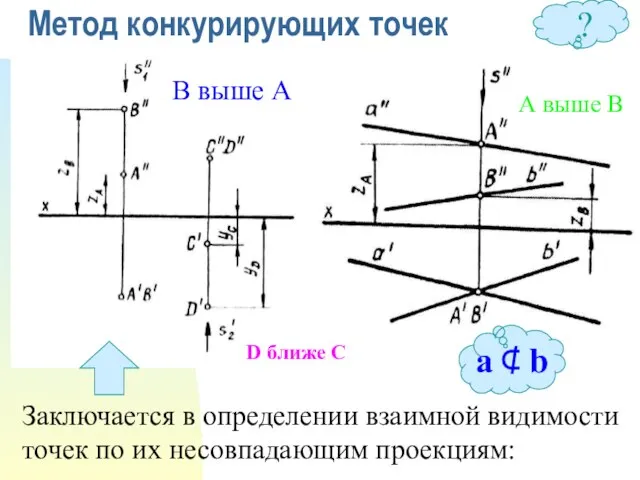
- 24. Метод конкурирующих точек Заключается в определении взаимной видимости точек по их несовпадающим проекциям: D ближе С
- 26. Скачать презентацию
 Секция «Проектирование учебного плана и программ дисциплин в области начального образования
Секция «Проектирование учебного плана и программ дисциплин в области начального образования Июль 2007
Июль 2007 Район Отрадное. Слайды
Район Отрадное. Слайды Презентация на тему Природные источники углеводородов
Презентация на тему Природные источники углеводородов  Бюджет семьи
Бюджет семьи Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п
Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин
Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин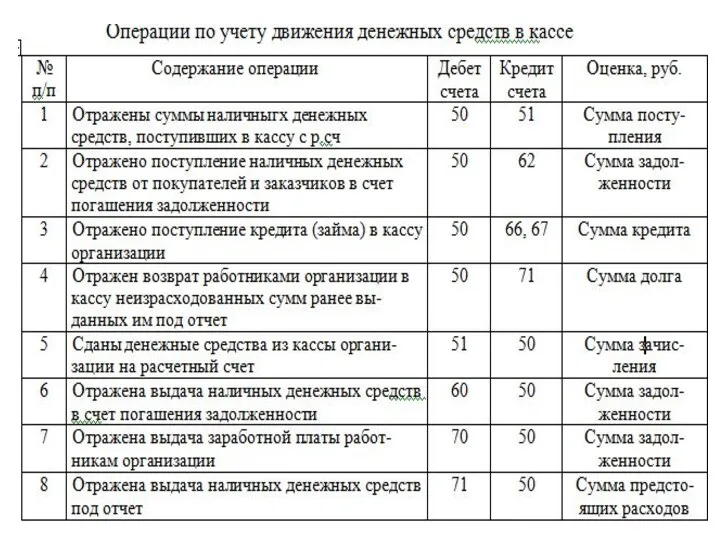 Операции по учету движения денежных средств в кассе
Операции по учету движения денежных средств в кассе Вниманию субъектов предпринимательства!
Вниманию субъектов предпринимательства! Перспективы развития информационных технологий в библиотечной сфере Хабаровского края
Перспективы развития информационных технологий в библиотечной сфере Хабаровского края Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО
Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО Презентация на тему история Крымской войны
Презентация на тему история Крымской войны  Искусство общения
Искусство общения Партии и идеологии современной России
Партии и идеологии современной России STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк
STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г
Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г Симметрия в цветочном мире
Симметрия в цветочном мире Виды изобразительного искусства
Виды изобразительного искусства Дания
Дания Творчество Б. Акунина
Творчество Б. Акунина Презентация на тему Домашние животные. Кто где живет?
Презентация на тему Домашние животные. Кто где живет?  Философско-методологические проблемы естествознания
Философско-методологические проблемы естествознания Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu.
Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu. «В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей
«В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей  我的朋友去外国旅游
我的朋友去外国旅游 Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру
Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру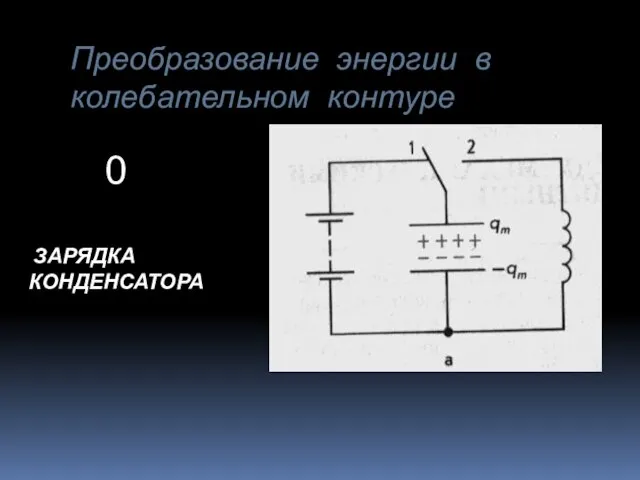 Презентация на тему Преобразование энергии в колебательном контуре
Презентация на тему Преобразование энергии в колебательном контуре  Ученическая научная конференция юных филологов «Дебют - 2011»
Ученическая научная конференция юных филологов «Дебют - 2011»