Слайд 2Название Вашего доклада
Определение линейного пространства

Слайд 3Колонтитул
Аксиомы линейного пространства

Слайд 6Колонтитул
Назовите нулевые элементы данных линейных пространств

Слайд 8Колонтитул
Базис линейного пространства и координаты вектора. Размерность линейного пространства

Слайд 10Колонтитул
и пусть имеет место другое разложение этого же вектора относительно этого же

базиса:
Вычтем (4) из (3):
Слайд 11Колонтитул
Теорема доказана.
Теорема 2. При сложении элементов линейного пространства их координаты в данном

базисе складываются. При умножении элемента на число его координаты умножаются на это число.
Слайд 16Колонтитул
Различие понятий линейной независимости векторов и базиса

Слайд 17Колонтитул
Размерность линейного пространства

Слайд 22Колонтитул
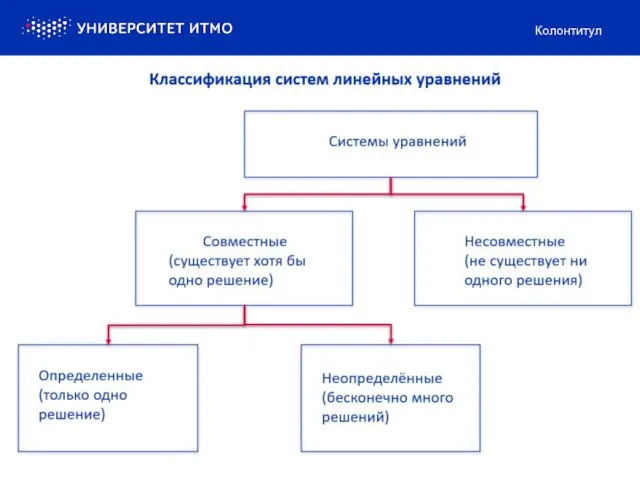
Системы линейных уравнений

Слайд 24Колонтитул
Совместная система – существует по крайней мере одно решение.
Несовместная система – не

существует решений.
Определенная система – имеет единственное решение
Неопределенная система – имеет более одного решения
Эквивалентные системы – множества решений совпадают.
Слайд 29Колонтитул
Алгоритм решения произвольной системы линейных уравнений





































 8 писем о конченном пути
8 писем о конченном пути Абстрактный пейзаж
Абстрактный пейзаж Отношения подростков и молодежи к сексуальным меньшинствам: принятие или отвержение
Отношения подростков и молодежи к сексуальным меньшинствам: принятие или отвержение Афоризмы
Афоризмы Содружество независимых государств 9 класс
Содружество независимых государств 9 класс Презентация на тему Вольга и Микула Селянинович
Презентация на тему Вольга и Микула Селянинович Місто Суми
Місто Суми Презентация на тему СПЕЦИФИЧНОСТЬ ПАРАЗИТОВ
Презентация на тему СПЕЦИФИЧНОСТЬ ПАРАЗИТОВ  Преобразования в области культуры и быта
Преобразования в области культуры и быта Презентация на тему Ассирийская держава Древний мир
Презентация на тему Ассирийская держава Древний мир  Домашнее задание по теме Прибыль и рентабельность
Домашнее задание по теме Прибыль и рентабельность «Фабрика Новостей»
«Фабрика Новостей» Угол. Прямой и развернутый угол
Угол. Прямой и развернутый угол Алкоголь
Алкоголь Использование продуктов JIRA и Confluence в компании Artezio
Использование продуктов JIRA и Confluence в компании Artezio Гражданское общество в России
Гражданское общество в России Образовательная система в Финляндии
Образовательная система в Финляндии Стыд, вина и извинения
Стыд, вина и извинения Центральная Избирательная Комиссия
Центральная Избирательная Комиссия Презентация по обществознанию на тему: демографическая ситуация в России и проблемы неполной семьи
Презентация по обществознанию на тему: демографическая ситуация в России и проблемы неполной семьи Ц.В.Церенов – заместитель директора Департамента корпоративного управления Минэкономразвития России
Ц.В.Церенов – заместитель директора Департамента корпоративного управления Минэкономразвития России Болгарская кухня в Санкт-Петербурге
Болгарская кухня в Санкт-Петербурге Творческий проект на тему экспресс курс «Оператор ЭВМ»
Творческий проект на тему экспресс курс «Оператор ЭВМ» ДОПОЛНИТЕЛЬНОЕОБРАЗОВАНИЕ КАК ПРОСТРАНСТВО УСПЕШНОЙ СОЦИАЛИЗАЦИИ ДЕТЕЙ
ДОПОЛНИТЕЛЬНОЕОБРАЗОВАНИЕ КАК ПРОСТРАНСТВО УСПЕШНОЙ СОЦИАЛИЗАЦИИ ДЕТЕЙ Презентация на тему Сталинград
Презентация на тему Сталинград  Трудовые ресурсы автотранспорта
Трудовые ресурсы автотранспорта Статистический анализ показателей национального богатства Российской Федерации
Статистический анализ показателей национального богатства Российской Федерации Инфобизнес. Что значит инфобизнес?
Инфобизнес. Что значит инфобизнес?