Содержание
- 2. Математическая логика. Булева алгебра Английский математик и логик. Профессор математики Королевского колледжа Корка (ныне Университетский колледж
- 3. Простые логические элементы
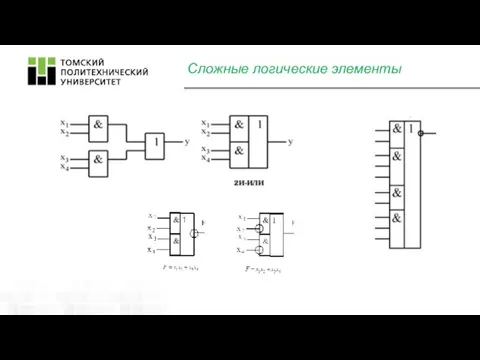
- 4. Сложные логические элементы
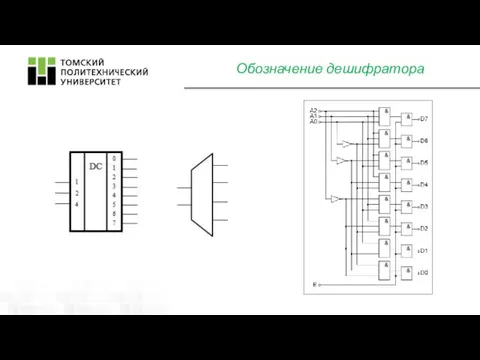
- 5. Обозначение дешифратора
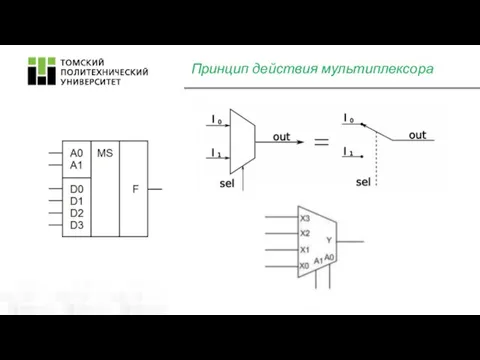
- 6. Принцип действия мультиплексора
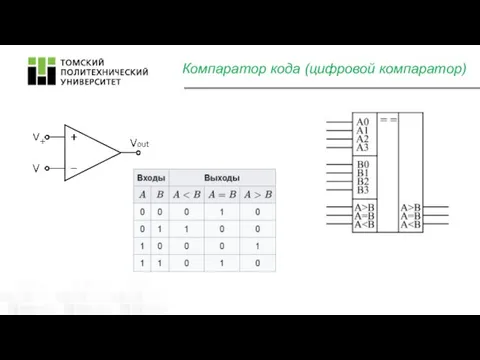
- 7. Компаратор кода (цифровой компаратор)
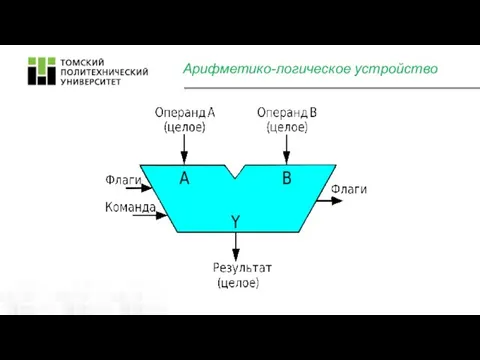
- 8. Арифметико-логическое устройство
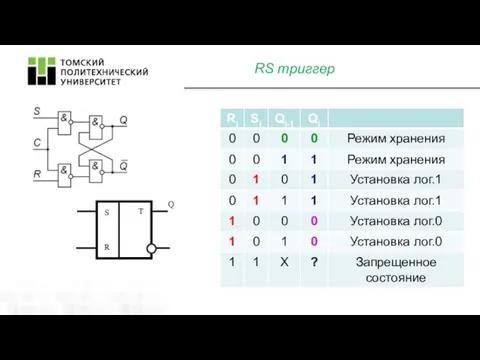
- 9. RS триггер
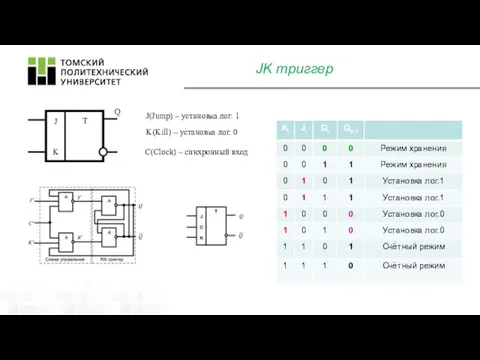
- 10. JK триггер J(Jump) – установка лог. 1 K(Kill) – установка лог. 0 C(Clock) – синхронный вход
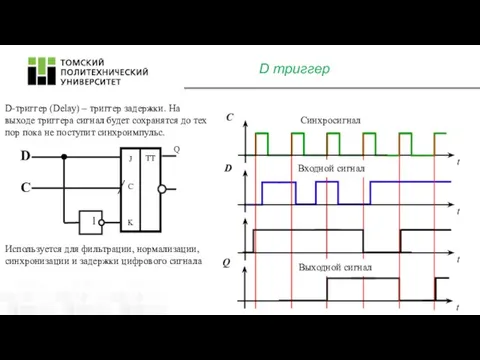
- 11. D триггер D-триггер (Delay) – триггер задержки. На выходе триггера сигнал будет сохранятся до тех пор
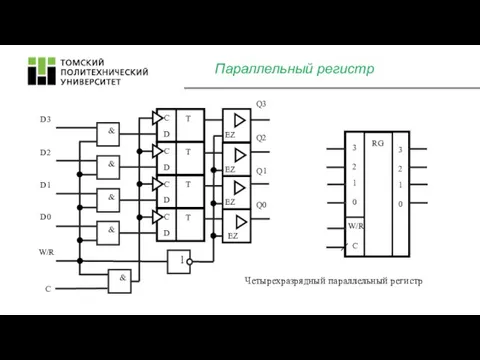
- 12. Параллельный регистр RG 3 2 1 0 3 2 1 0 W/R C Четырехразрядный параллельный регистр
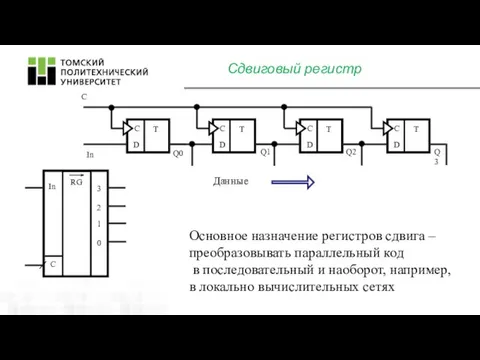
- 13. Сдвиговый регистр С RG In 3 2 1 0 C In Данные Основное назначение регистров сдвига
- 14. Счётчик прямой
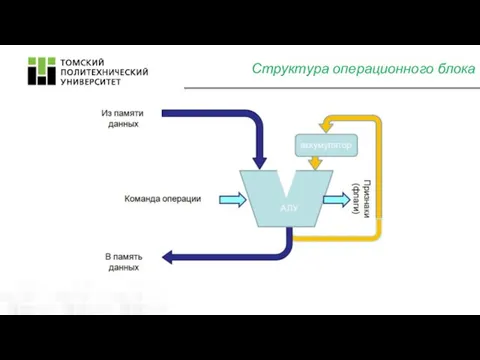
- 15. Структура операционного блока
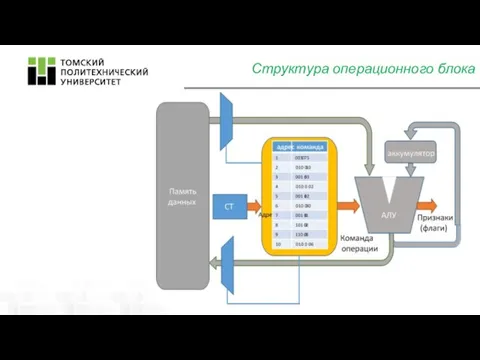
- 17. Структура операционного блока
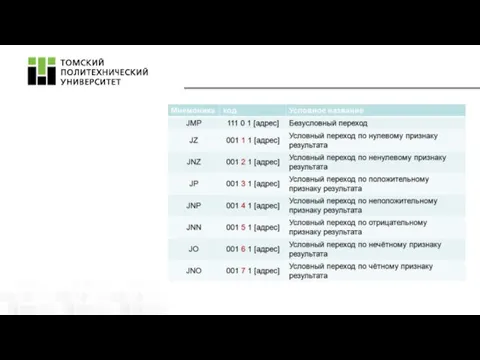
- 18. Условные и безусловные переходы Условные переходы позволяют выполнить ветвление алгоритма в зависимости от результатов промежуточных расчётов.
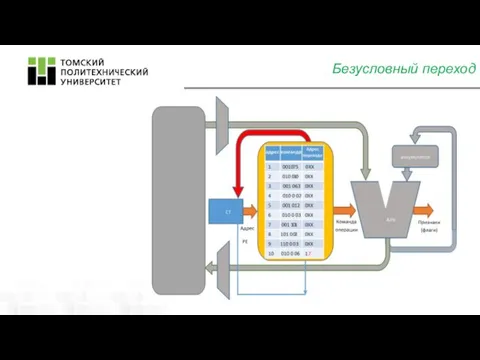
- 19. Безусловный переход
- 22. Скачать презентацию





 Сбербанк онлайн
Сбербанк онлайн Единицы длины, денежные единицы, меры массы «Счёт и вычисления – основа порядка в голове» И.Песталоцци
Единицы длины, денежные единицы, меры массы «Счёт и вычисления – основа порядка в голове» И.Песталоцци Творческие работы, фотографии
Творческие работы, фотографии Назначение и проведение пожарно-технической экспертизы
Назначение и проведение пожарно-технической экспертизы Arenta. Смарт-офис
Arenta. Смарт-офис Неметаллы
Неметаллы Процесс совершенствования системы управления конфликтами в организации
Процесс совершенствования системы управления конфликтами в организации Понятия коррупция и противодействие коррупции
Понятия коррупция и противодействие коррупции Эскизы мотивов вышивки
Эскизы мотивов вышивки Презентация опыт3
Презентация опыт3 Математик - бизнесмен
Математик - бизнесмен Північна Америка
Північна Америка Традиции и обычаи татар
Традиции и обычаи татар Презентация на тему Кожа и ее значение (4 класс)
Презентация на тему Кожа и ее значение (4 класс) Библиоинновации
Библиоинновации Права потребителя
Права потребителя Образы и мотивы в орнаментах русской народной вышивки (5 класс)
Образы и мотивы в орнаментах русской народной вышивки (5 класс) Корпоративный проект "Сводная база данных "Край":лингвистическое обеспечение
Корпоративный проект "Сводная база данных "Край":лингвистическое обеспечение Степени сравнения прилагательных
Степени сравнения прилагательных Творческое объединение лего-мастерская Шелезяка. Робототехника
Творческое объединение лего-мастерская Шелезяка. Робототехника Основные направления бюджетной и налоговой политики Пермского края на 2018 - 2020-е годы
Основные направления бюджетной и налоговой политики Пермского края на 2018 - 2020-е годы The Rolling Stones
The Rolling Stones  Образ дороги в русской живописи XIX века
Образ дороги в русской живописи XIX века оТЧЕТ о работЕ ШМО учителей математики, информатики, технологии
оТЧЕТ о работЕ ШМО учителей математики, информатики, технологии 20170502_znat_geografiyu-_znachit_pobedit_0
20170502_znat_geografiyu-_znachit_pobedit_0 «ВСЕ В ТВОИХ РУКАХ»
«ВСЕ В ТВОИХ РУКАХ» Древние славяне
Древние славяне Театр масок
Театр масок