Лобанов Алексей Иванович

Становление – конец XIX века
Карл Рунге
Алексей Николаевич Крылов

Основные задачи
Физические модели – дифференциальные уравнения
Приближенное решение нелинейных дифференциальных уравнений или систем

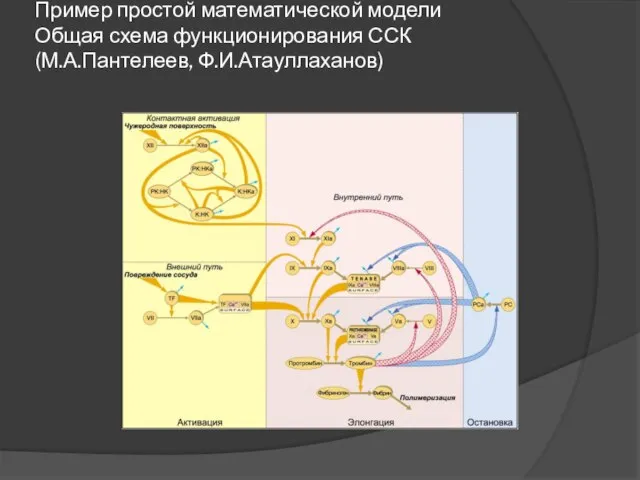
Пример простой математической модели
Общая схема функционирования ССК
(М.А.Пантелеев, Ф.И.Атауллаханов)

Пример простой математической модели
Система в частных производных без учета конвективных потоков

Проблемы
Непрерывная задача – дискретная задача
Качество приближения
АППРОКСИМАЦИЯ

Проблемы
Действительное число (бесконечная десятичная дробь) – операции с конечной длиной мантиссы
Ошибки округления
УСТОЙЧИВОСТЬ

Проблемы
Корректность постановки – непрерывная зависимость от начальных данных
ОБУСЛОВЛЕННОСТЬ

Погрешности
Пусть u и u* — точное и приближенное значение некоторой величины соответственно. Тогда абсолютной погрешностью приближения u* называется величина ∆, удовлетворяющая неравенству

Погрешности
Относительной погрешностью называется величина
удовлетворяющая неравенству
Обычно используется запись

Погрешности
Машинный эпсилон
машинным ε называют наибольшее из чисел, для которых в рамках используемой системы вычислений выполнено 1 + ε = 1

1. Задача численного дифференцирования
Пусть задана таблица значений xi. В дальнейшем совокупность точек на отрезке, котором проводятся вычисления, иногда будут называться сеткой, каждое значение xi — узлом сетки. Пусть сетка равномерная, и расстояние между узлами равно — шагу сетки. Пусть узлы сетки пронумерованы в порядке возрастания

1. Задача численного дифференцирования
Производная
Конечная разность
(1)

1. Задача численного дифференцирования
Погрешность формулы (1)
Пусть f – проекция на сетку дважды непрерывно дифференцированной функции, тогда

1. Задача численного дифференцирования
Полная погрешность

1. Задача численного дифференцирования
Оптимальный шаг дифференцирования

1. Задача численного дифференцирования
Формула второго порядка
(2)

1. Задача численного дифференцирования
Оптимальный шаг для формулы второго порядка (2)

1. Задача численного дифференцирования
Вычисление второй производной

1. Задача численного дифференцирования
Метод неопределенных коэффициентов
Введем на рассматриваемом отрезке шаблон из нескольких точек

1. Задача численного дифференцирования
Раскладываем в ряд Тейлора в окрестности x

1. Задача численного дифференцирования
Система линейных уравнений метода неопределенных коэффициентов
…

Система
1. Задача численного дифференцирования

1. Задача численного дифференцирования
Определитель данной матрицы — детерминант Вандермонда. Из курса линейной алгебры известно, что он не равен нулю. Тогда существует единственный набор коэффициентов α, который позволяет найти на шаблоне из (1 + l + m) точек значение первой производной с точностью

1. Задача численного дифференцирования
Для нахождения второй производной можно использовать ту же самую формулу с небольшой модификацией

1. Задача численного дифференцирования
Система уравнений