Логика

Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древнегреческими мыслителями.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы речи от ее содержания. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления

Логика - наука о формах и способах мышления
Законы логики отражают в сознании человека
свойства
связи
отношения
объектов окружающего мира

Формы Мышления
Понятие
Высказывание
Умозаключение

Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.
Между множествами (объемами понятий) могут быть различные виды отношений:
· равнозначность, когда объемы понятий полностью совпадают;
· пересечение, когда объемы понятий частично совпадают;
· подчинения, когда объем одного понятия полностью входит в объем другого и т.д
Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используются диаграммы Эйлера-Венна.

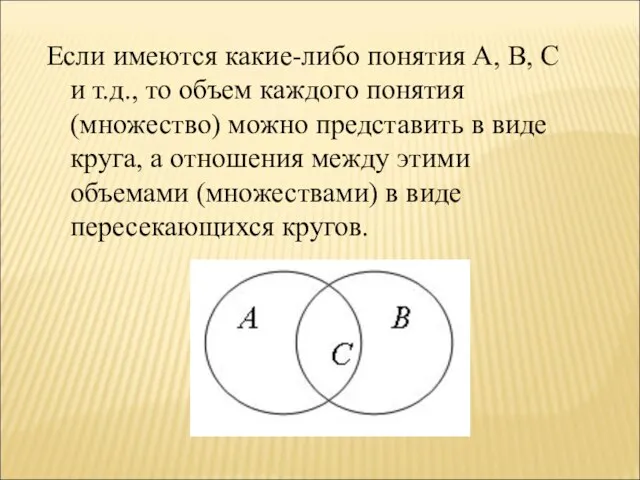
Если имеются какие-либо понятия A, B, C и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объемами (множествами) в виде пересекающихся кругов.

ОТОБРАЗИТЬ С ПОМОЩЬЮ ДИАГРАММЫ ЭЙЛЕРА-ВЕННА СООТНОШЕНИЕ МЕЖДУ ОБЪЕМАМИ ПОНЯТИЙ НАТУРАЛЬНЫЕ ЧИСЛА И ЧЕТНЫЕ ЧИСЛА.
Объем понятия натуральные числа включает в себя множество целых положительных чисел А
Объем понятия четные числа включает в себя множество отрицательных и положительных четных чисел В.
Эти множества пересекаются, т.к. включают в себя множество положительных четных чисел С.

- это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.
Высказывание

Высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения:
1 - ИСТИНА
0 - ЛОЖЬ

Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей.
Ложным суждение будет в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности.

Обоснование истинности или ложности простых высказываний решается вне алгебры логики.
Например, истинность или ложность высказывания: "Сумма углов треугольника равна 180 градусов" устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным

Умозаключение
- это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

Умозаключения бывают:
1. дедуктивные,
2. индуктивные
3. по аналогии.
В дедуктивных умозаключениях рассуждения ведутся от общего к частному.
Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна».

В индуктивных умозаключениях рассуждения ведутся от частного к общему.
Например, установив, что отдельные металлы - железо, медь, цинк, алюминий и т.д. - обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны.

Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений.
Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле.

САМОСТОЯТЕЛЬНОЕ ЗАДАНИЕ
1. Отобразить с помощью диаграммы Эйлера-Венна соотношения между следующими объемами понятий:
а) целые и натуральные числа;
б) четные и нечетные числа

2. Приведите примеры понятий, суждений, умозаключений и доказательств из различных наук: математики; информатики; физики и химии.

Основные понятия математической логики
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности и ложности) и логических операций над ними
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно
Для обозначения истины (истинного высказывания) используется символ 1 (True), а для обозначения лжи (ложного высказывания) используется символ 0 (False).
True = 1 False = 0
True > False

Примеры логических выражений

Что такое логические выражения?
Логическое выражение – это некоторое высказывание, по поводу которого можно заключить истинно оно или ложно.
Логическое выражение , подобно математическому выражению выполняется (вычисляется), но в результате получается не число, а логическое значение (логическая величина)

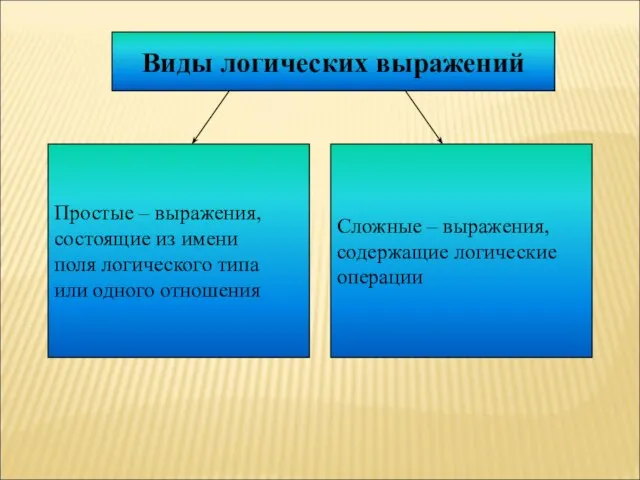
Виды логических выражений
Простые – выражения,
состоящие из имени
поля логического типа
или одного отношения
Сложные – выражения,
содержащие логические
операции

Примеры простых высказываний
Шесть первых выражений называются отношениями.

Осадки = «дождь» 5. Автор = «Толстой Л.Н.»
Давление > 740 6. Фамилия = «Русанов»
Влажность <> 100 7. Цветоводство
Полка < 5 8. Танцы
Знаки отношений :
= равно
<> не равно
> больше
< меньше
>= больше или равно
<= меньше или равно

ОТНОШЕНИЯ
Отношения – это выражения в которых имена полей базы данных связываются в соответствующие знаки отношений

Особенности выполнения отношений для символьных величин.
Отношение «равно» истинно для двух символьных величин, если их длина одинакова и все соответствующие символы совпадают
Символьные величины можно сопоставлять и в отношениях <, >, <=, >= по принципу: сравниваются между собой не сами символы, а их внутренние коды

Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить более сложные высказывания. Такие слова и словосочетания называют логическими связками.
Сложные логические выражения
Сложные логические выражения состоят из простых, с помощью логических операций (связок)

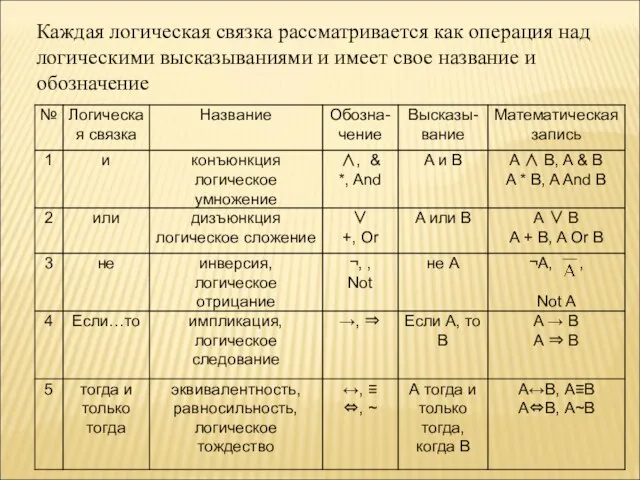
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение

Логическое умножение
Обозначение :
в русском языке – и
в английском языке – and
в математической логике - /\
В результате логического умножения получается истина, если
оба операнда (логические величины) истинны.

Логическое сложение
Обозначение :
в русском языке – или
в английском языке – or
в математической логике - \/
В результате логического сложение получается истина, если значение хотя бы одного операнда истинно

Логическое отрицание
Обозначение :
в русском языке – не
в английском языке – not
в математической логике - x
Отрицание изменяет значение логического выражения на противоположное.
Отрицание – одноместная операция, она применяется к одному логическому операнду

Порядок действий
Not (отрицание)
And (логическое умножение)
Or (логическое сложение)
>,=,<

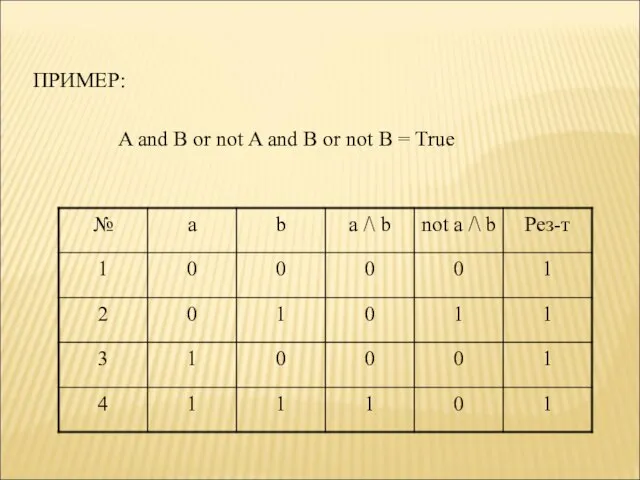
ПРИМЕР:
A and B or not A and B or not B = True