Логико-математическое моделирование и прогнозирование социальной динамики: методологические проблемыС.Ю.Малков, В.И.Ковалев Ак
Содержание
- 2. Для составления обоснованного прогноза нужны модели, позволяющие получать количественные оценки (то есть математические модели). Однако достаточно
- 3. Процессы социальной самоорганизации: формирование социальных структур а) эквифинальных (слабо зависящих от начальных условий, но зависящих от
- 4. Динамическое моделирование социальной самоорганизации Пусть X – вектор переменных, характеризующих состояние общества, тогда их изменение может
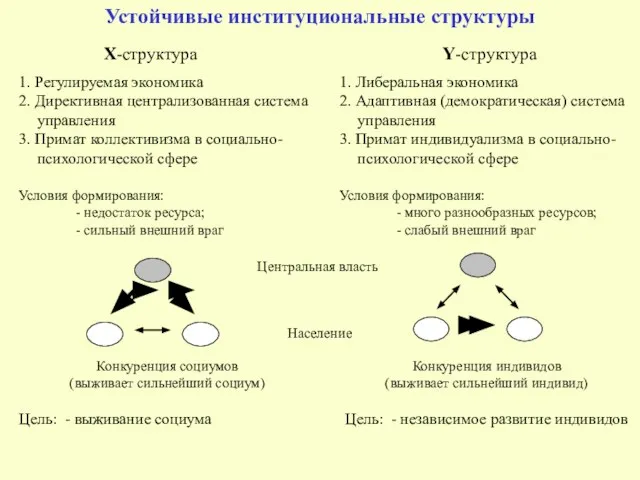
- 5. Устойчивые институциональные структуры X-структура Y-структура 1. Регулируемая экономика 2. Директивная централизованная система управления 3. Примат коллективизма
- 6. X-структура Цель: - выживание социума Способ достижения цели: - объединение слабых вокруг сильного (сильная центральная власть)
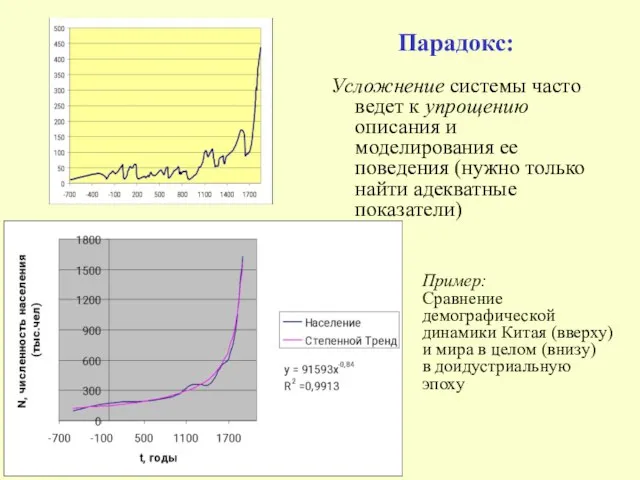
- 7. Возможность выявления «параметров порядка» в динамике сложных систем Пример: Модель глобального демографического роста Население (показатель –
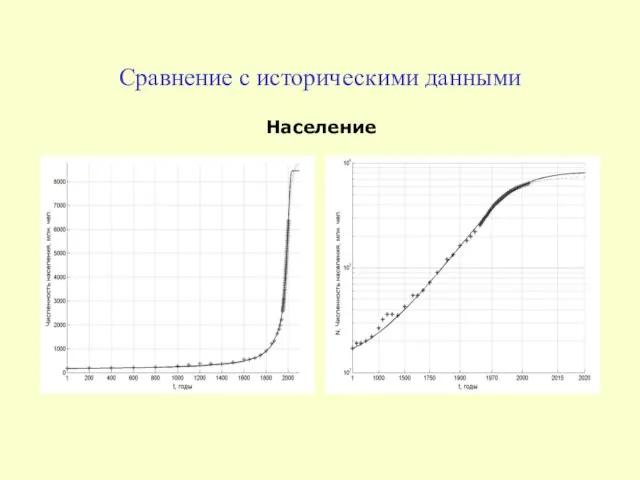
- 8. Сравнение с историческими данными Население
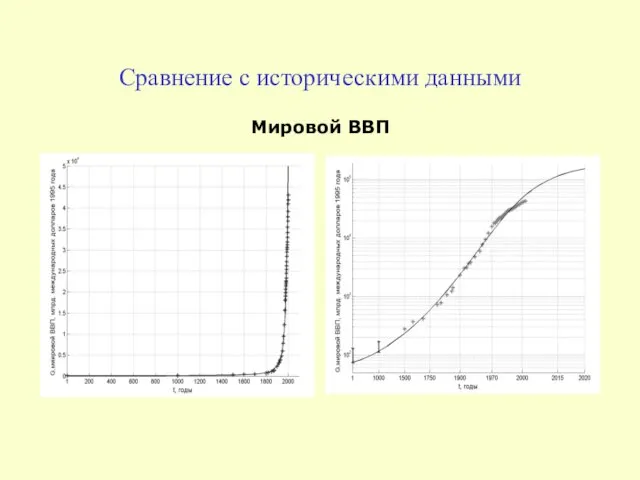
- 9. Сравнение с историческими данными Мировой ВВП
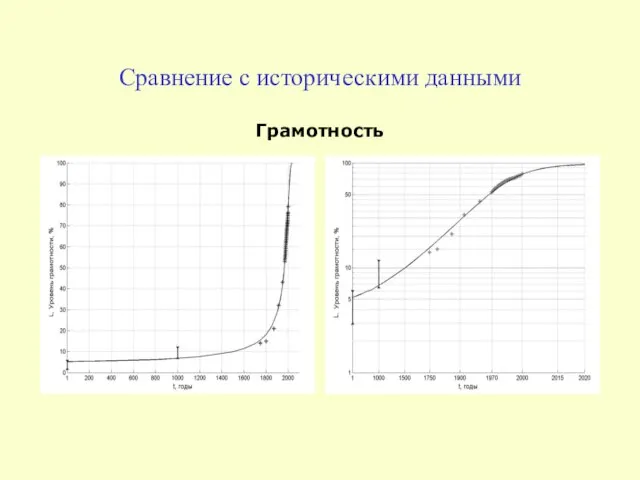
- 10. Сравнение с историческими данными Грамотность
- 11. Парадокс: Усложнение системы часто ведет к упрощению описания и моделирования ее поведения (нужно только найти адекватные
- 12. Вывод: Создание общих моделей социально-экономического развития на высокоагрегированном уровне (отражающих законы истории), по-видимому, возможно. Проблема: В
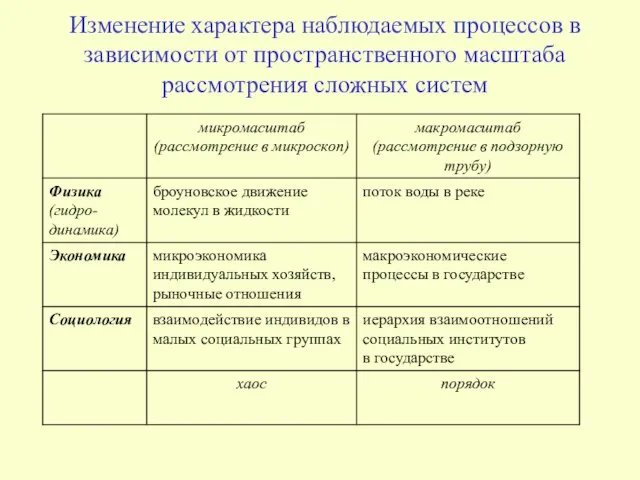
- 13. Изменение характера наблюдаемых процессов в зависимости от пространственного масштаба рассмотрения сложных систем
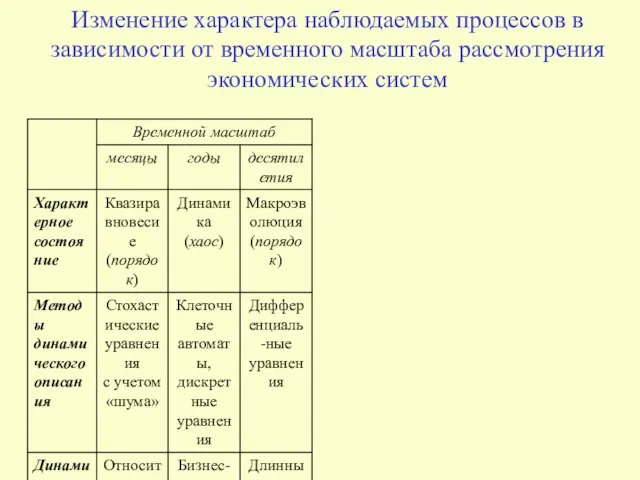
- 14. Изменение характера наблюдаемых процессов в зависимости от временного масштаба рассмотрения экономических систем
- 15. - Нужно уметь «сшивать» модели разного уровня, хотя это сложно - Локальная хаотизированность динамики социально-экономических процессов,
- 16. Проблема проверки создаваемых социальных моделей может быть решена на основе ретропрогноза. В истории нельзя поставить эксперимент,
- 18. Скачать презентацию








 Особенности погружения свай в мерзлые грунты
Особенности погружения свай в мерзлые грунты Кольцо Всевластия
Кольцо Всевластия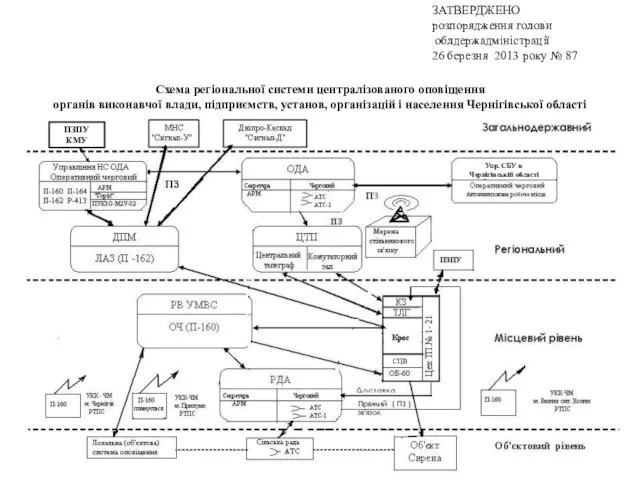 Схема регіональної системи централізованого оповіщення органів виконавчої влади, підприємств, установ
Схема регіональної системи централізованого оповіщення органів виконавчої влади, підприємств, установ Совместные программы, как инструмент интеграции российских вузов в европейское пространство высшего образования C.М. Яковлев, к
Совместные программы, как инструмент интеграции российских вузов в европейское пространство высшего образования C.М. Яковлев, к Transport Layer
Transport Layer  Педагогический советГОУ СОШ № 552
Педагогический советГОУ СОШ № 552 Акватории Московской области
Акватории Московской области Презентация на тему Поэма Гомера Илиада
Презентация на тему Поэма Гомера Илиада  Презентация на тему ПОЛЯРНЫЕ ЖИВОТНЫЕ
Презентация на тему ПОЛЯРНЫЕ ЖИВОТНЫЕ  Tuapse Refinery
Tuapse Refinery Приемы устного счета. Умножение
Приемы устного счета. Умножение Federalism timeline
Federalism timeline  Объединения. Отделение дополнительного образования детей на 2021-2022 учебный год. Начальная школа
Объединения. Отделение дополнительного образования детей на 2021-2022 учебный год. Начальная школа Сталинградская битва17 июля 1942 - 2 февраля 1943
Сталинградская битва17 июля 1942 - 2 февраля 1943 Требования к составлению основной общеобразовательной программы основного общего образования
Требования к составлению основной общеобразовательной программы основного общего образования Виды искусств
Виды искусств Пошив изделий по готовым выкройкам
Пошив изделий по готовым выкройкам О конкурсах Лучший в сфере потребительского рынка Ленинградской области в 2020 году
О конкурсах Лучший в сфере потребительского рынка Ленинградской области в 2020 году Процессоры
Процессоры КРК ЭТАЛОНКомплексные Решения Контроля
КРК ЭТАЛОНКомплексные Решения Контроля Память компьютера – совокупность устройств хранения информации
Память компьютера – совокупность устройств хранения информации History of London
History of London  Джаспер Моррисон. Биография и творческий путь
Джаспер Моррисон. Биография и творческий путь Цветовой круг. Цветотипы внешности
Цветовой круг. Цветотипы внешности АКТУАЛЬНО ВЫПУСКАЕМЫЕ ИЗДЕЛИЯ DIPLOMAT 2011 Ассортимент установок и кресел Дипломат Стоматологические установки: Стационарные Диплома
АКТУАЛЬНО ВЫПУСКАЕМЫЕ ИЗДЕЛИЯ DIPLOMAT 2011 Ассортимент установок и кресел Дипломат Стоматологические установки: Стационарные Диплома Люди взрослые, папы и мамы!Пообщайтесь с нами!Дети просят:Прочитайте нам сказки,Проверьте уроки.Дети ждут от вас ласки,Вы не будьте
Люди взрослые, папы и мамы!Пообщайтесь с нами!Дети просят:Прочитайте нам сказки,Проверьте уроки.Дети ждут от вас ласки,Вы не будьте  Грузовые автомобили Mercedes-Benz. Обозначение моделей и описание технологий
Грузовые автомобили Mercedes-Benz. Обозначение моделей и описание технологий ПОРТФОЛИОучителя начальных классовЛитвиновой Эльвиры Александровны
ПОРТФОЛИОучителя начальных классовЛитвиновой Эльвиры Александровны