Содержание
- 2. The aim of the work: To explore the history of the emergence and development of magic
- 3. Historical reference The country, which was first coined by the magic square, just unknown, unknown age,
- 4. Historical reference During the archeological excavations in China and India there were found square amulets. The
- 5. Definition 1. Magic box - this is a sequence of numbers from 1 to n2, located
- 6. Table of calculation of the frequency of occurrence» to magic squares n≥ 3
- 7. Method ‘Terraces’ This paragraph is devoted to the method of terraces. Method terraces was offered by
- 8. The figure has numbers from 1 to 25 in the natural order slashes (diagonal) rows from
- 10. Скачать презентацию
Слайд 2The aim of the work:
To explore the history of the emergence and
The aim of the work:
To explore the history of the emergence and

development of magic squares, learn basic methods of magic squares.
Tasks of the work:
Analyze the literature and the Internet resources of the origin, definition, types of magic squares.
Describe all the magic squares n=1,2, 3.
Compare the «frequency of occurrence of the» magic square of order n≥3.
Clarification of the method Bahe and the way of filling magic squares.
Tasks of the work:
Analyze the literature and the Internet resources of the origin, definition, types of magic squares.
Describe all the magic squares n=1,2, 3.
Compare the «frequency of occurrence of the» magic square of order n≥3.
Clarification of the method Bahe and the way of filling magic squares.
Слайд 3Historical reference
The country, which was first coined by the magic square, just
Historical reference
The country, which was first coined by the magic square, just
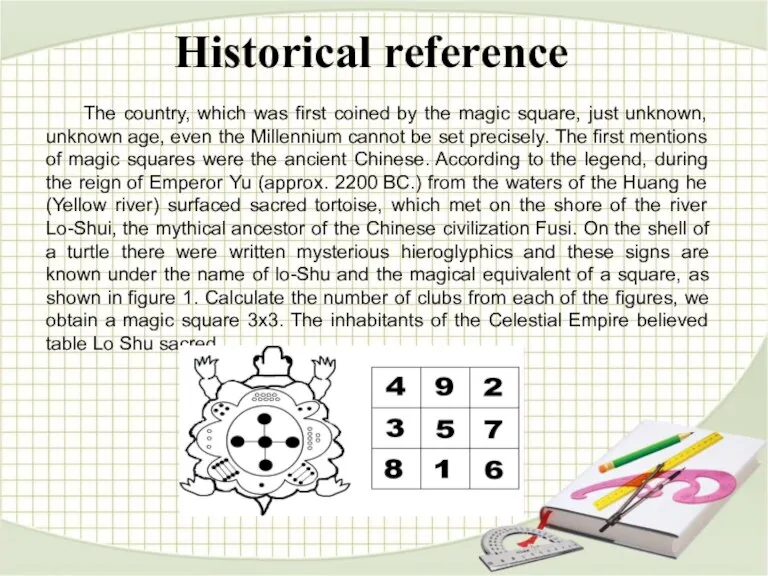
unknown, unknown age, even the Millennium cannot be set precisely. The first mentions of magic squares were the ancient Chinese. According to the legend, during the reign of Emperor Yu (approx. 2200 BC.) from the waters of the Huang he (Yellow river) surfaced sacred tortoise, which met on the shore of the river Lo-Shui, the mythical ancestor of the Chinese civilization Fusi. On the shell of a turtle there were written mysterious hieroglyphics and these signs are known under the name of lo-Shu and the magical equivalent of a square, as shown in figure 1. Calculate the number of clubs from each of the figures, we obtain a magic square 3x3. The inhabitants of the Celestial Empire believed table Lo Shu sacred.
Слайд 4Historical reference
During the archeological excavations in China and India there were found
Historical reference
During the archeological excavations in China and India there were found
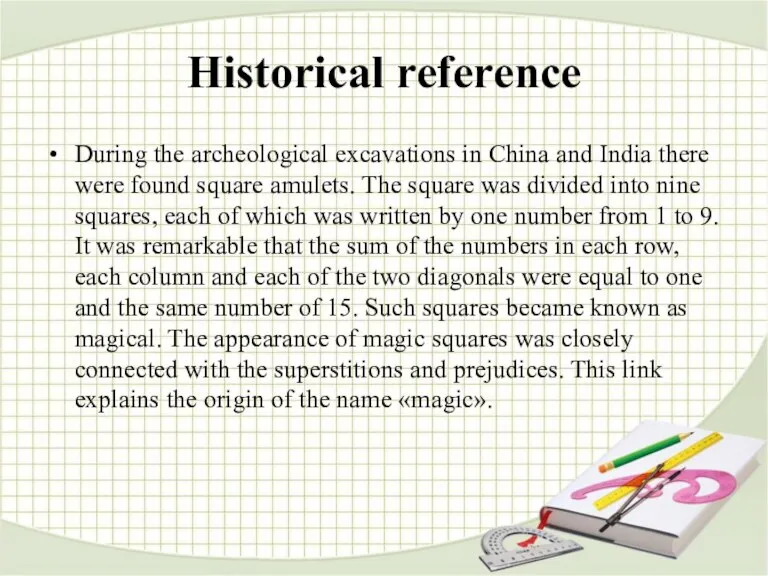
square amulets. The square was divided into nine squares, each of which was written by one number from 1 to 9. It was remarkable that the sum of the numbers in each row, each column and each of the two diagonals were equal to one and the same number of 15. Such squares became known as magical. The appearance of magic squares was closely connected with the superstitions and prejudices. This link explains the origin of the name «magic».
Слайд 5Definition 1. Magic box - this is a sequence of numbers from
Definition 1. Magic box - this is a sequence of numbers from
1 to n2, located on the ruled square, so that the sum of the numbers in all the rows, columns and on both diagonals of the squares have the same value, and called the magic of the amount.
Formula magical amount
For each of n, where ‘n’ is the magic square, the value of the magic of the amount S can be determined by formula.
The sum of numbers in each line is equal to S, and lines of a total of ‘n’, it means that the sum of all numbers magic square is equal to n*S.
On the other hand, according to the formula for the sum of n terms of an arithmetical progression, we find that the same amount is equal to 1+2+3+...+n2= (1+n2) n2/2.
Equal these two values, we get n*S= (1+n2)n2/2.
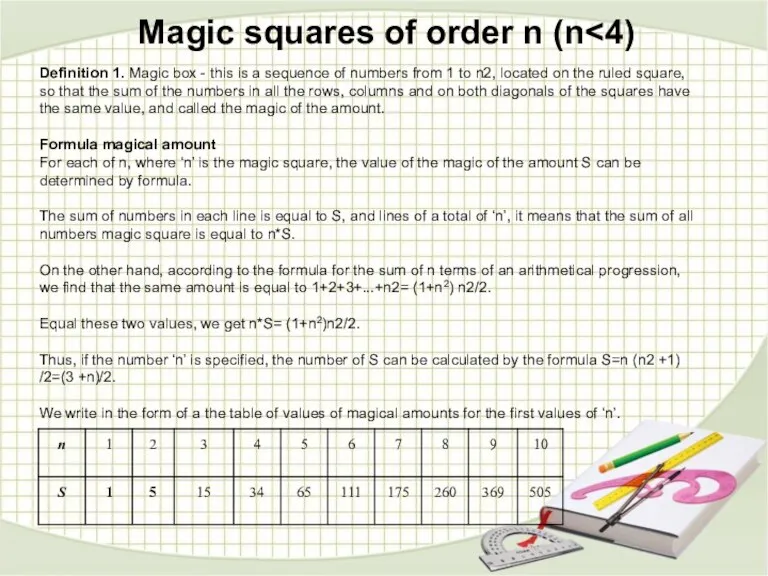
Thus, if the number ‘n’ is specified, the number of S can be calculated by the formula S=n (n2 +1) /2=(3 +n)/2.
We write in the form of a the table of values of magical amounts for the first values of ‘n’.
Formula magical amount
For each of n, where ‘n’ is the magic square, the value of the magic of the amount S can be determined by formula.
The sum of numbers in each line is equal to S, and lines of a total of ‘n’, it means that the sum of all numbers magic square is equal to n*S.
On the other hand, according to the formula for the sum of n terms of an arithmetical progression, we find that the same amount is equal to 1+2+3+...+n2= (1+n2) n2/2.
Equal these two values, we get n*S= (1+n2)n2/2.
Thus, if the number ‘n’ is specified, the number of S can be calculated by the formula S=n (n2 +1) /2=(3 +n)/2.
We write in the form of a the table of values of magical amounts for the first values of ‘n’.
Magic squares of order n (n<4)
Слайд 7Method ‘Terraces’
This paragraph is devoted to the method of terraces. Method terraces
Method ‘Terraces’
This paragraph is devoted to the method of terraces. Method terraces
was offered by Claude Gaspard Bachet, Sieur de Mezirial (1581 - 1638) and therefore it was called the method of Rascals. In 1612 Bashe published a collection of interesting tasks. Great interest was caused by the publication of them in 1621, «Arithmetic» of Diophantus in Greek and in own translation into Latin, with a lot of comments. This translation became a Handbook and source of new discoveries for Pierre Fermat, and other outstanding mathematicians of the seventeenth century; it is at the margins of this book Fermat wrote the wording of its Great theorem.
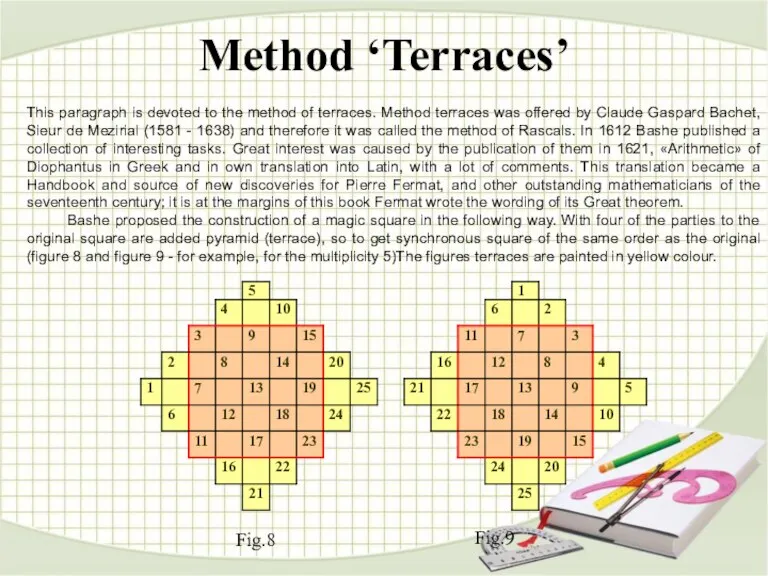
Bashe proposed the construction of a magic square in the following way. With four of the parties to the original square are added pyramid (terrace), so to get synchronous square of the same order as the original (figure 8 and figure 9 - for example, for the multiplicity 5)The figures terraces are painted in yellow colour.
Bashe proposed the construction of a magic square in the following way. With four of the parties to the original square are added pyramid (terrace), so to get synchronous square of the same order as the original (figure 8 and figure 9 - for example, for the multiplicity 5)The figures terraces are painted in yellow colour.
Fig.8
Fig.9
Слайд 8The figure has numbers from 1 to 25 in the natural order
The figure has numbers from 1 to 25 in the natural order
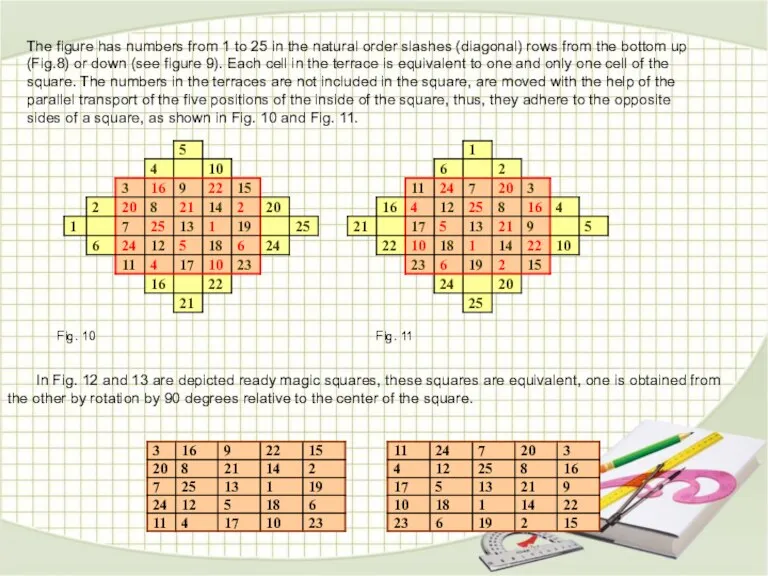
slashes (diagonal) rows from the bottom up (Fig.8) or down (see figure 9). Each cell in the terrace is equivalent to one and only one cell of the square. The numbers in the terraces are not included in the square, are moved with the help of the parallel transport of the five positions of the inside of the square, thus, they adhere to the opposite sides of a square, as shown in Fig. 10 and Fig. 11.
Fig. 10 Fig. 11
In Fig. 12 and 13 are depicted ready magic squares, these squares are equivalent, one is obtained from the other by rotation by 90 degrees relative to the center of the square.
- Предыдущая
London. Sightseeing of LondonСледующая -
The Abc party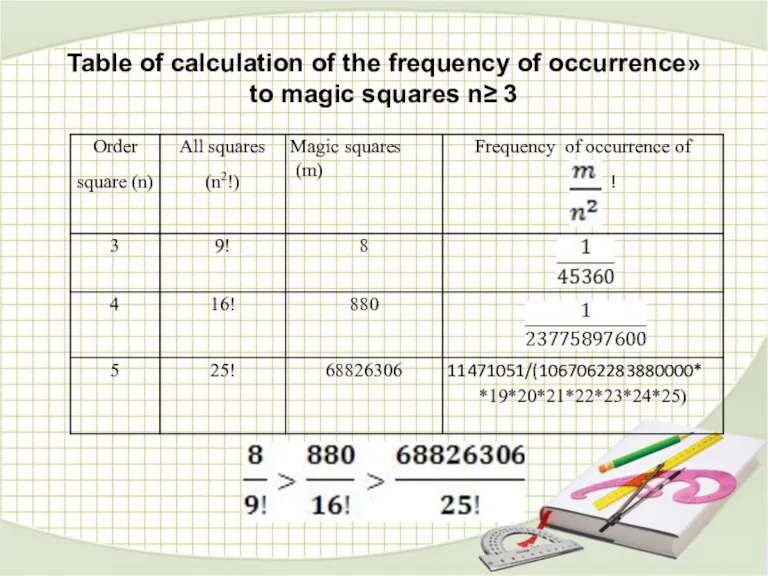
 Урок математики в 5 классе
Урок математики в 5 классе Искусство и духовная жизнь
Искусство и духовная жизнь Сны и сновидения
Сны и сновидения Questel databases Information & Analytical Solution Использование для патентных исследований, конкурентной разведки, маркетинговых исследований, оцен
Questel databases Information & Analytical Solution Использование для патентных исследований, конкурентной разведки, маркетинговых исследований, оцен Компьютеры будущего
Компьютеры будущего Презентация на тему Человек и земная кора
Презентация на тему Человек и земная кора Презентация на тему Синтаксис. Прямая речь
Презентация на тему Синтаксис. Прямая речь Александр Македонский
Александр Македонский Зачем изучать русский язык ?
Зачем изучать русский язык ? Презентация на тему Дети – герои России
Презентация на тему Дети – герои России Добрышев Евгений Николаевич
Добрышев Евгений Николаевич Автор: Плеханова Ю. И.
Автор: Плеханова Ю. И. Рацион стройности. Продукты включения и исключения
Рацион стройности. Продукты включения и исключения Синхронизация отправления и прибытия грузов различными видами транспорта в перевалочных пунктах. Задача 1
Синхронизация отправления и прибытия грузов различными видами транспорта в перевалочных пунктах. Задача 1 Любителям горячих завтраков – просто, быстро, вкусно, недорого!
Любителям горячих завтраков – просто, быстро, вкусно, недорого! По блоку с планировками
По блоку с планировками Стратегический и операционный маркетинг Детерминанты стратегического маркетинга
Стратегический и операционный маркетинг Детерминанты стратегического маркетинга Мониторинг качества и доступностигосударственных услуг – 2011
Мониторинг качества и доступностигосударственных услуг – 2011 Презентация на тему Деревянные матрёшки-разноцветные одёжки
Презентация на тему Деревянные матрёшки-разноцветные одёжки ООО «Агентство АВИАФРАХТ ПЛЮС»
ООО «Агентство АВИАФРАХТ ПЛЮС» Калейдоскоп интересных задач
Калейдоскоп интересных задач Должностная инструкция
Должностная инструкция Патриоты земли Нижегородской
Патриоты земли Нижегородской Презентация на тему Арифметические действия над числами
Презентация на тему Арифметические действия над числами  Уральская драматургия
Уральская драматургия Gоршки от Vовочки. Проект
Gоршки от Vовочки. Проект Образование
Образование БОЛГАРИЯ
БОЛГАРИЯ