Содержание
- 2. MAPLE Преобразования чисел с разным основанием В Maple возможна работа с числами, имеющими различное основание. Помимо
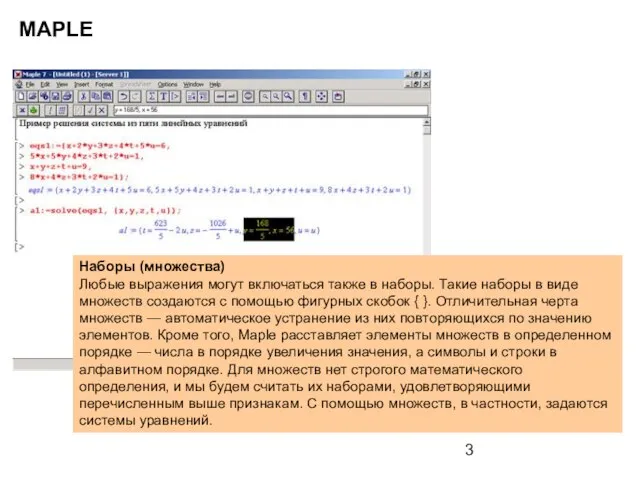
- 3. MAPLE Наборы (множества) Любые выражения могут включаться также в наборы. Такие наборы в виде множеств создаются
- 4. MAPLE Списки выражений Для создания упорядоченных наборов — списков — служат квадратные скобки [ ]: >
- 5. MAPLE Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется
- 6. MAPLE Таблицы Еще одним важным типом множественных данных являются таблицы. Они задают данные с произвольной индексацией.
- 7. MAPLE Строки и комментарии Строковые данные Строки как тип данных — это просто цепочки символов. Они
- 8. MAPLE Константы Константы - это простейшие именованные объекты, несущие заранее предопределенные значения. Их имена (идентификаторы) также
- 9. MAPLE Переменные — это объекты, значения которых могут меняться по ходу выполнения документа. Тип переменной может
- 10. MAPLE Операторы Имеется пять основных типов операторов: - binary — бинарные операторы (двумя операндами); - unary
- 11. MAPLE Операторы Для данных типа «множество» определены следующие бинарные операторы: union — включает первый операнд (множество)
- 12. MAPLE Операторы Логические операторы: « » - Больше; «>=» - Большее или равно; «=» - Равно;
- 13. MAPLE Операторы Специальные типы операторов: композиционные («@»); функциональные («var -> result» или « »); неопределенные и
- 14. MAPLE Математические функции Понятие о встроенных функциях Maple имеет полный набор элементарных математических функций. Все они,
- 15. MAPLE Математические функции В ядре Maple реализован полный набор тригонометрических и гиперболических функций, а также их
- 16. MAPLE Математические функции Функции с элементами сравнения В алгоритме вычисления ряда функций заложено сравнение результата с
- 17. MAPLE Функции работы с массивами, векторами и матрицами Вызов элемента и присваивание ему значений: V[i]:=x —
- 18. MAPLE Примеры матричных вычислений: Функции работы с массивами, векторами и матрицами
- 19. MAPLE Примеры символьных вычислений с матрицами. Функция map(fname, M, x) позволяет выполнить функцию fname над всеми
- 20. MAPLE Работа со строковыми данными Обработка строк Имеется ряд функций для работы со строками. Из них
- 21. MAPLE Пользовательские функции и средства программирования Для повышения эффективности работы с Maple возникает необходимость в создании
- 22. MAPLE Пользовательские функции и средства программирования Еще один способ задания функции пользователя базируется на применении функции
- 23. MAPLE Пользовательские функции и средства программирования Важный класс функций – импликативные, в которых связь между переменными
- 24. MAPLE Пользовательские функции и средства программирования Как и любой другой язык программирования Maple-язык содержит набор операторов,
- 26. Скачать презентацию
Слайд 2MAPLE
Преобразования чисел с разным основанием
В Maple возможна работа с числами, имеющими различное
MAPLE
Преобразования чисел с разным основанием В Maple возможна работа с числами, имеющими различное

двоичные (основание 2 — binary),
восьмеричные (основание 8 — octal), - шестнадцатеричные (основание 16 — hex).
Функция convert позволяет легко преобразовывать форматы чисел.
Эта функция может преобразовывать в числа и строковые выражения.
Слайд 3MAPLE
Наборы (множества)
Любые выражения могут включаться также в наборы. Такие наборы в виде
MAPLE
Наборы (множества) Любые выражения могут включаться также в наборы. Такие наборы в виде
Слайд 4MAPLE
Списки выражений
Для создания упорядоченных наборов — списков — служат квадратные скобки [
MAPLE
Списки выражений Для создания упорядоченных наборов — списков — служат квадратные скобки [

> [10, 2+3, 4+4, 8, 5, 1]:
[10, 5, 8, 8, 5, 1]
Элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц.
В ряде случаев, например при подготовке данных для двумерных графиков, возникает необходимость в подготовке парных списков — скажем, координат точек (х, у) графика. Для этого можно использовать функцию zip(f, u, v) или zip(f, u, v, d). Здесь f — бинарная функция, u, v — списки или векторы, d — необязательный параметр.
Слайд 5MAPLE
Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array.
MAPLE
Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array.

- аrrау[а. .b,s1] — возвращает вектор с индексами от а до b и значениями в одномерном списке s1; - аrrау[а. .b,c. .d,s2] — возвращает матрицу с номерами строк от а до b, номерами столбцов от с до d и значениями в двумерном списке s2.
Двумерные списки часто путают с матрицами. Векторы и матрицы создаются с помощью функции array и являются отдельным типом данных. Элементами векторов и массивов могут быть константы, переменные, выражения, списки и иные объекты. Эти элементы являются индексированными переменными и их положение указывается индексами. Размерность массивов, создаваемых списками, не ограничена и массивы могут быть многомерными. Имеется множество функций для работы со списками, массивами и матрицами.
Слайд 6MAPLE
Таблицы
Еще одним важным типом множественных данных являются таблицы. Они задают данные
MAPLE
Таблицы
Еще одним важным типом множественных данных являются таблицы. Они задают данные

Пустая таблица резервирует память под данные. Когда параметром функции table является список выражений, он выводится в естественном порядке расположения элементов таблицы, но с произвольным порядком индексации.
Можно выделить отдельные компоненты таблицы и вывести значения и индексы таблицы с помощью функций entries и indices.
Слайд 7MAPLE
Строки и комментарии
Строковые данные
Строки как тип данных — это просто цепочки символов.
MAPLE
Строки и комментарии Строковые данные Строки как тип данных — это просто цепочки символов.

В других случаях последовательность символов рассматривается как строка, если она заключена в обратные апострофы, то есть в знаки '. Два апострофа подряд формируют апостроф как знак символьной строки, например `abc``def ` дает строку abc`def. Любое математическое выражение может входить в строку и при этом не выполняется:
> '2+2 не всегда "четыре"';
2+2 не всегда 'четыре'
Неисполняемые программные комментарии Часто возникает необходимость в задании программных комментариев. Любой текст после знака # рассматривается как невыводимый (неисполняемый) программный комментарий — даже если это математическое выражение. При этом он не вычисляется. Например:
> 2+3; #Это пример. А это выражение не вычисляется: 4+5 5
Комментарии полезны в программах на Maple-языке и обычно используются для объяснения особенностей реализованных алгоритмов.
Слайд 8MAPLE
Константы
Константы - это простейшие именованные объекты, несущие заранее предопределенные значения. Их имена
MAPLE
Константы Константы - это простейшие именованные объекты, несущие заранее предопределенные значения. Их имена

В выражениях часто встречаются литералы – это неименованные числовые константы. В выражении 2*sin(1.25) числа 2 и 1.25 являются числовыми литералами. Строковыми константами являются произвольные цепочки символов, заключенные в обратные апострофы, например 'Hello', 'Привет', 'My number‘. Числа, заключенные в апострофы, например '123456', также становятся строковыми константами, которые нельзя использовать в арифметических выражениях.
Встроенные в ядро константы
Есть также ряд констант, которые правильнее считать заведомо определенными глобальными переменными:
false — логическое значение «ложно»; gamma — константа Эйлера, равная 0.5772156649...; infinity — положительная бесконечность (отрицательная задается как -infinity); true — логическое значение «истинно»; Catalan — константа Каталана, равная 0.915965594...; FAIL — специальная константа (см. справку, выдаваемую по команде ?FAIL); I — мнимая единица (квадратный корень из -1); Pi — представляет константу = 3.141...
В этот список не входит основание натурального логарифма — число е. В качестве этой константы рекомендуется использовать ехр(1). Она отображается как жирная прямая буква Е. A exp(1.) выводит 2.71828... (что и следовало ожидать). Идентификация констант
Функции type(х, constant) и type(x, realcons) возвращают логическое значение true, если х представляет целочисленную или вещественную константу, и false, если х не является константой.
Слайд 9MAPLE
Переменные — это объекты, значения которых могут меняться по ходу выполнения документа.
MAPLE
Переменные — это объекты, значения которых могут меняться по ходу выполнения документа.

Не допускается использовать в качестве имен переменных зарезервированные слова, имена предопределенных констант и функций. Чтобы проверить уникальность вводимого идентификатора можно выполнить команду ?name, где name – выбранный идентификатор переменной.
По умолчанию любые переменные рассматриваются как объекты символьного типа. Благодаря этому такие переменные могут фигурировать в математических выражениях (таких, как sin(x)/x) без их предварительного объявления – это не влечет за собой появления сообщений об ошибках и является более естественным. Для присваивания переменным конкретных значений используется комбинированный символ присваивания «:=».
Если значение переменной определено с помощью оператора присваивания, то такие переменные не могут использоваться в символьных вычислениях. Для придания статуса неопределенных переменных необходимо либо вызвать команду restart (тогда все ранее определенные переменные станут неопределенными), либо выполнить оператор x:=‘x’;, либо использовать функцию x:=evaln(x);.
Слайд 10MAPLE
Операторы
Имеется пять основных типов операторов:
- binary — бинарные операторы (двумя операндами);
MAPLE
Операторы
Имеется пять основных типов операторов:
- binary — бинарные операторы (двумя операндами);

- unary — унарные операторы (с одним операндом);
- nullary — нульарные операторы (без операнда — это одна, две и три пары кавычек);
- precedence — операторы старшинства (включая логические операторы);
- functional — функциональные операторы.
Бинарные операторы:
«+» - Сложение; «-» - Вычитание; «*» - Умножение; «/» - Деление; «**» или «^» - Возведение в степень; «mod» - Остаток от деления; «$» - Оператор последовательности; «.» - Разделительная точка; «@» - Оператор композиции; «@@» - Повторение композиции; «,» - Разделитель выражений; «:=» - Присваивание; «..» - Задание интервала; «||» - Конкатенация (объединение) строк.
Слайд 11MAPLE
Операторы
Для данных типа «множество» определены следующие бинарные операторы:
union — включает первый
MAPLE
Операторы
Для данных типа «множество» определены следующие бинарные операторы:
union — включает первый

intersect — создает множество, содержащее общие для операндов элементы;
minus — исключает из первого операнда элементы второго операнда.
В любом случае, в результирующем множестве устраняются повторяющиеся элементы.
Оператор композиции @@ может использоваться для создания сложных функций, содержащих цепные дроби.
В примере используется функциональный оператор «->», задающий пользовательскую функцию.
Специальный оператор % обеспечивает подстановку в строку ввода (или в выражение) последнего результата операции, %% — предпоследнего и %%% — третьего с конца.
Слайд 12MAPLE
Операторы
Логические операторы:
«<» - Меньше; «<=» - Меньше или равно; «>» - Больше;
MAPLE
Операторы
Логические операторы:
«<» - Меньше; «<=» - Меньше или равно; «>» - Больше;

Результатом вычисления выражения с логическими операторами являются логические константы true или false, если оно не выполняется.
Кроме того, к логическим операторам относится унарный оператор «not» — он представляет логическое «нет».
Для возврата логических значений выражений с этими операторами используется функция evalb(условие).
Логические операторы часто используются в управляющих структурах программ, составленных на языке программирования Maple.
Слайд 13MAPLE
Операторы
Специальные типы операторов:
композиционные («@»);
функциональные («var -> result» или « var>»);
var>»);
неопределенные и инертные («&name»);
заданные с помощью команды define(name, свойство1, свойство2,….)
time() – системная функция, показывающая время в секундах, затраченное на выполнение указанного в скобках оператора.
MAPLE
Операторы
Специальные типы операторов: time() – системная функция, показывающая время в секундах, затраченное на выполнение указанного в скобках оператора.
композиционные («@»);
функциональные («var -> result» или «
неопределенные и инертные («&name»);
заданные с помощью команды define(name, свойство1, свойство2,….)
Слайд 14MAPLE
Математические функции
Понятие о встроенных функциях
Maple имеет полный набор элементарных математических функций.
MAPLE
Математические функции
Понятие о встроенных функциях
Maple имеет полный набор элементарных математических функций.

Целочисленные функции, используемые в теории чисел:
factorial(n) — функция вычисления факториала (альтернатива — оператор !);
iquo(a.b) — целочисленное деление а на b;
irem(a,b) — остаток от деления а на b;
igcd(a b) — наибольший общий делитель;
lcm(a,b) — наименьшее общее кратное.
Слайд 15MAPLE
Математические функции
В ядре Maple реализован полный набор тригонометрических и гиперболических функций, а
MAPLE
Математические функции
В ядре Maple реализован полный набор тригонометрических и гиперболических функций, а

К степенным и логарифмическим относятся следующие функции Maple:
ехр — экспоненциальная функция; ilog10 — целочисленный логарифм по основанию 10 (возвращает целую часть от логарифма по основанию 10);
ilog — целочисленный логарифм (библиотечная функция, возвращающая целую часть от натурального логарифма); ln — натуральный логарифм;
log — логарифм по заданному основанию (библиотечная функция);
log10 — логарифм по основанию 10; sqrt — квадратный корень.
Слайд 16MAPLE
Математические функции
Функции с элементами сравнения
В алгоритме вычисления ряда функций заложено сравнение
MAPLE
Математические функции
Функции с элементами сравнения
В алгоритме вычисления ряда функций заложено сравнение

abs — абсолютное значение числа;
ceil — наименьшее целое, большее или равное аргументу;
floor — наибольшее целое, меньшее или равное аргументу;
frac — дробная часть числа;
trunc — целое, округленное в направлении нуля;
round — округленное значение числа;
signum(х) — знак х (-1 при х < 0, 0 при х = 0 и +1 при х > 0).
Для комплексного аргумента х эти функции определяются следующим образом:
tranc(x) = trunc(Re(x)) + I*trunc(Im(x));
round(x) = round(Re(x)) + I*round(Im(x));
frac(x) - frac(Re(x)) + I*frac(Im(x)).
flооr(x) = floor(Re(x)) + I*floor(Im(x)) + X, где
ceil(x) = -flооr(-х)
Специальные математические функции обычно являются решениями линейных дифференциальных уравнений различного типа и выражаются в виде интегралов, не представимых через элементарные функции. Maple имеет практически полный набор таких функций. Их представления можно найти в справочной базе данных Maple.
Слайд 17MAPLE
Функции работы с массивами, векторами и матрицами
Вызов элемента и присваивание ему значений:
V[i]:=x
MAPLE
Функции работы с массивами, векторами и матрицами
Вызов элемента и присваивание ему значений:
V[i]:=x

M[i,j]:=x — присваивание нового значения х элементу матрицы М.
Векторы и матрицы похожи на списки, но не полностью отождествляются с ними. Используя функцию преобразования данных convert, можно преобразовывать одномерные списки в векторы, а двумерные списки — в матрицы.
Функция type(V, vector) — тестирует аргумент V и возвращает true, если V — вектор, и false в ином случае; type(M,matrix) — тестирует аргумент М и возвращает true, если М — матрица, и false в ином случае.
Для проведение вычислений с массивами и матрицами используется функция evalm(M)
Слайд 18MAPLE
Примеры матричных вычислений:
Функции работы с массивами, векторами и матрицами
MAPLE
Примеры матричных вычислений:
Функции работы с массивами, векторами и матрицами

Слайд 19MAPLE
Примеры символьных вычислений с матрицами.
Функция map(fname, M, x) позволяет выполнить функцию
MAPLE
Примеры символьных вычислений с матрицами.
Функция map(fname, M, x) позволяет выполнить функцию

Функции работы с массивами, векторами и матрицами
Слайд 20MAPLE
Работа со строковыми данными
Обработка строк
Имеется ряд функций для работы со строками.
MAPLE
Работа со строковыми данными
Обработка строк
Имеется ряд функций для работы со строками.

lenght(str) — возвращает число символов, содержащихся в строке str;
substring(str, a, b) — возвращает подстроку строки str от а-го символа до b-го;
cat(strl,str2....) — возвращает строку, полученную объединением строк str1, str2,... (альтернатива — оператор конкатенации в виде точки .);
SearchText(s, str) — производит поиск подстроки s в строке str и при его успехе возвращает номер позиции s в строке str (при отсутствии s в str функция возвращает 0).
Интерактивный ввод математических выражений с запросом:
функция readstat(promt), где promt — строка с текстовым комментарием.
Ввод строкового выражения с последующим преобразованием его в математическое выражение с помощью функции parse
Слайд 21MAPLE
Пользовательские функции и средства программирования
Для повышения эффективности работы с Maple возникает необходимость
MAPLE
Пользовательские функции и средства программирования
Для повышения эффективности работы с Maple возникает необходимость

Самый простой способ – присвоить некоторой переменной выражение и в дальнейшем его использовать, как функцию.
Заданный таким образом объект все же не является полноценной функцией пользователя, поскольку в нем используются только глобальные переменные (х и у) и нет объявленного списка параметров, от которых зависит значение функции. При этом значения переменных функции приходится заведомо задавать отдельно, используя операции присваивания.
Для задания полноценных функций пользователя применяется функциональный оператор. При этом используется следующая конструкция: name:=(x,y,...)->expr.
После этого вызов функции осуществляется в виде name(x.y,...), где (х.у,...) — список формальных параметров функции пользователя с именем name. Переменные, указанные в списке формальных параметров, являются локальными. При подстановке на их место фактических параметров они сохраняют их значения только в теле функции (ехрr). За пределами этой функции переменные с этими именами оказываются либо неопределенными, либо сохраняют ранее присвоенные им значения.
Слайд 22MAPLE
Пользовательские функции и средства программирования
Еще один способ задания функции пользователя базируется на
MAPLE
Пользовательские функции и средства программирования
Еще один способ задания функции пользователя базируется на
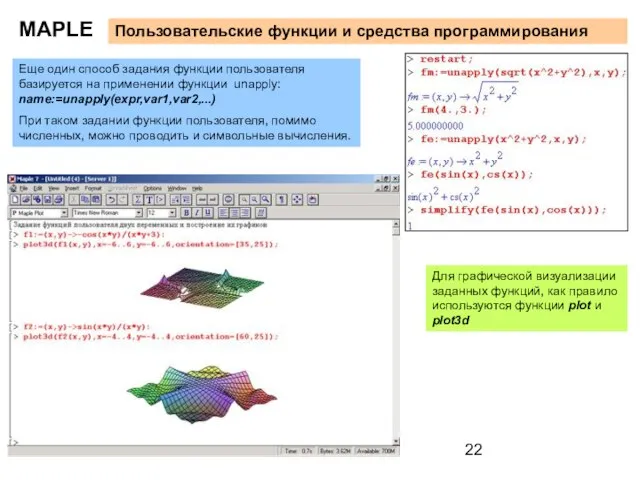
При таком задании функции пользователя, помимо численных, можно проводить и символьные вычисления.
Для графической визуализации заданных функций, как правило используются функции plot и plot3d
Слайд 23MAPLE
Пользовательские функции и средства программирования
Важный класс функций – импликативные, в которых связь
MAPLE
Пользовательские функции и средства программирования
Важный класс функций – импликативные, в которых связь
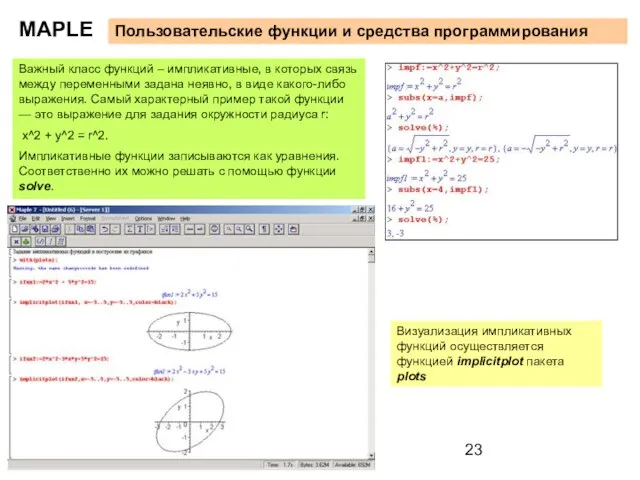
х^2 + у^2 = r^2.
Импликативные функции записываются как уравнения. Соответственно их можно решать с помощью функции solve.
Визуализация импликативных функций осуществляется функцией implicitplot пакета plots
Слайд 24MAPLE
Пользовательские функции и средства программирования
Как и любой другой язык программирования Maple-язык содержит
MAPLE
Пользовательские функции и средства программирования
Как и любой другой язык программирования Maple-язык содержит

Условный оператор: if (условие) then Элементы_1 else Элементы_2 fi;
Оператор цикла: for
Процедуры
Можно задать некоторую последовательность действий в виде отдельной процедуры:
name := рroc(Формальные_параметры) Тело процедуры end;
Вызов осуществляется в любом месте: name(Фактические параметры);
Используя оператор return(Значение), можно явно указать значение, возвращаемое процедурой. Если return опущен, то процедура возвращает значение, полученное в последнем выражении тела.
 Кондратий Федорович Рылеев
Кондратий Федорович Рылеев Богоматерь Донская
Богоматерь Донская Правотворческая деятельность в Российской Федерации
Правотворческая деятельность в Российской Федерации Энергоаудит
Энергоаудит Схемы технологии нагнетания пара. Зямилова А.А
Схемы технологии нагнетания пара. Зямилова А.А Виды разборов. Повторение
Виды разборов. Повторение Хэллоуин (31октября)
Хэллоуин (31октября) КОНКУРС ЧТЕЦОВ «МОЙ УЧИТЕЛЬ»
КОНКУРС ЧТЕЦОВ «МОЙ УЧИТЕЛЬ» Взаимовлияние Современных Интернет-Технологий и МЛС в Соединенных Штатах Америки Светлана Столярова, Local-n-Global Realty USA, Cleveland OH REALTOR® Member of National Association of REALTORS® - NAR Ohio Association of REALTORS® - OAR Clevelan
Взаимовлияние Современных Интернет-Технологий и МЛС в Соединенных Штатах Америки Светлана Столярова, Local-n-Global Realty USA, Cleveland OH REALTOR® Member of National Association of REALTORS® - NAR Ohio Association of REALTORS® - OAR Clevelan Презентация на тему Топливно-энергетический комплекс России
Презентация на тему Топливно-энергетический комплекс России  Незнание закона не освобождает от ответственности
Незнание закона не освобождает от ответственности Восстановление и ретуширование фотографий
Восстановление и ретуширование фотографий Моделирование учетных процессов
Моделирование учетных процессов Наш проект. Создание
Наш проект. Создание Различение частицы и приставки НЕ
Различение частицы и приставки НЕ Традиционная еда
Традиционная еда Террасная доска из ДПК от производителя
Террасная доска из ДПК от производителя Децентрализованная система искусственного интеллекта Daisy
Децентрализованная система искусственного интеллекта Daisy 20140121_prezentatsiya_tsr_9_klass
20140121_prezentatsiya_tsr_9_klass Управление конфликтами в проекте
Управление конфликтами в проекте Wild and farm animals
Wild and farm animals Спиридон Дмитриевич Дрожжин
Спиридон Дмитриевич Дрожжин История праздника "День народного единства"
История праздника "День народного единства" МОУ Шокшинская средняя общеобразовательная школа
МОУ Шокшинская средняя общеобразовательная школа Путешествие по осеннему лесу - презентация для начальной школы_
Путешествие по осеннему лесу - презентация для начальной школы_ Реклама в Интернете
Реклама в Интернете Your health
Your health