Математическая логика и формы мышления

Связь логики и вычислительной техники
Логика является теоретической основой современных ЭВМ и сложных управляющих систем. Используя методы и средства логической науки, ученые разрабатывают эффективные языки программирования.
Особое значение логическая наука стала приобретать в вопросах, касающихся проблемы искусственного интеллекта. Именно здесь разработчикам пришлось создать новую область логических исследований – логический анализ.

Связь логики и вычислительной техники
Внутри машины все числа (а так же информация другого рода: буквы, знаки и др.) представлена в виде двоичных кодов. При выполнении программы арифметическо-логическое устройство (АЛУ) производит различные операции над двоичными числами, выдавая результаты также в виде двоичных чисел. Поэтому АЛУ можно рассматривать как сложный функциональный преобразователь, на вход которого поступают исходные двоичные числа, а на выходе выдаётся новое двоичное число, являющееся той или иной функцией от входных чисел.

Логика.
Запишите определение логики:
Опр: Логика – (logos (др. гр.) – слово, мысль, понятие, закон, рассуждение) – наука о законах и формах мышления.
Основоположник – Аристотель (384-322гг до н.э). Рассмотрел мышление со стороны строения, структуры, т.е. с формальной стороны. Так возникла формальная логика.

Логика.
Формальная логика – наука, пытавшаяся найти ответ на вопрос, как мы рассуждаем, изучающая логические операции и правила мышления.
Основоположник математической логики – нем.математик, философ Вильгельм Лейбниц (XVII в.). Первый пытался построить логические исчисления: арифметические и буквенно-алгебраические; высказал мысль о возможности применения двоичной СС в вычислительной математике.
Дальнейшее развитие его идеи получили лишь в XIXв. В трудах математика Джорджа Буля, отца писательницы Э. Войнич. Он вывел для логических построений особую алгебру – алгебру логики.
Опр: Раздел математики, занимающийся исследованием логических функций, называется алгеброй логики.

Вильгельм Готфрид Лейбниц
Вильгельм Готфрид Лейбниц родился в 1646 году в семье философа, профессора университета в городе Лейпциге. Став взрослым и получив университетское образование, Лейбниц поступил на дипломатическую службу. Поездки в Париж и Лондон дали ему возможность ознакомиться с идеями великих математиков Франции и Англии. В 1676 году Лейбниц завязал переписку с Ньютоном. К сожалению, она продолжалась только год и не привела к объединению усилий.
Научное соперничество и взаимная неприязнь Ньютона и Лейбница породили вопрос, который много лет волновал историков и политиков: кто же все-таки был первооткрывателем? Вероятно, Ньютон придумал основные понятия дифференциального и интегрального исчислений чуть раньше - зато Лейбниц первым опубликовал свои результаты, и к тому же применил более удобную, чем у Ньютона, систему обозначений. Эти обозначения математики используют уже более трёхсот лет.

Аристотель
АРИСТОТЕЛЬ (ок. 384–322 до н.э.), древнегреческий философ и педагог, родился в Стагире в 384 или 383 до н.э., умер в Халкиде в 322 до н.э. Почти двадцать лет Аристотель учился в Академии Платона и, по-видимому, какое-то время там преподавал.
Аристотель регулярно читал своим ученикам и помощникам лекции по самым разнообразным предметам.
Труды Аристотеля можно разделить по следующим группам:
Во-первых, это труды по логике, обычно собирательно именуемые Органон. Сюда входят Категории; Об истолковании; Первая аналитика и Вторая аналитика; Топика.
Во-вторых, Аристотелю принадлежат естественнонаучные труды. В-третьих, мы располагаем сводом текстов под названием Метафизика, представляющим собой цикл лекций. В-четвертых, имеются труды по этике и политике.
Философия Аристотеля. Аристотель нигде не говорит, что логика является частью собственно философии. Он воспринимает ее скорее в качестве методологического инструмента всех наук и философии, а не самостоятельного философского учения. Понятно, что логика должна предшествовать философии.

Джордж Буль
Родился в семье рабочего. Первые уроки математики получил у отца. Хотя мальчик посещал местную школу, его можно считать самоучкой. В 12 лет знал латынь, затем овладел греческим, французским, немецким и итальянским языками. В 16 лет уже преподавал в деревенской школе, а в 20 открыл собственную школу в Линкольне.
В 1854 году опубликовал работу «Исследование законов мышления, базирующихся на математической логике и теории вероятностей». Работы 1847 и 1854 годов положили начало алгебре логики, или булевой алгебре. Буль первым показал, что существует аналогия между алгебраическими и логическими действиями, так как и те, и другие предполагают лишь два варианта ответов – истина или ложь, нуль или единица. Он придумал систему обозначений и правил, пользуясь которыми можно было закодировать любые высказывания, а затем манипулировать ими как обычными числами. Булева алгебра располагала тремя основными операциями – И, ИЛИ, НЕ, которые позволяли производить сложение, вычитание, умножение, деление и сравнение символов и чисел. Таким образом, Булю удалось подробно описать двоичную систему счисления. В своей работе «Законы мышления» (1854 г.) Буль окончательно сформулировал основы математической логики. Он также попытался сформулировать общий метод вероятностей, с помощью которого из заданной системы вероятных событий можно было бы определить вероятность последующего события, логически связанного с ними.

Логика.
Главная задача логики - выявить, какие способы рассуждения правильные, а какие нет; описать и исследовать те способы рассуждений, которые являются правильными.
Пример неправильного рассуждения …

Основные понятия логики.
Логика рассматривает три различные формы мышления, в которых осуществляется мышление: понятие, суждение, умозаключение.
Запишите определение:
Понятие – мысль, в которой обобщаются и выделяются предметы некоторого класса по определенным, общим и в совокупности специфическим для них признакам.

Основные понятия логики.
Каждая мысль выражается словами в предложении, которые представляют собой различные суждения (высказывания):
Запишите определение:
Суждением (высказыванием) называется всякое утверждение (или всякое предложение), о котором можно судить, истинно оно или ложно. Истинное высказывание обозначается - 1, ложное - 0
«6 - четное число» - это высказывание, т.к. оно истинное.
«Рим - столица Франции» - это тоже высказывание т.к. оно ложное.

Основные понятия логики.
Запишите определение:
Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (предпосылок, условий) выводится новое суждение (заключение, вывод).

Вывод умозаключений
Путь вывода умозаключений лежит через …
Рассуждение – это цепочка взаимосвязанных суждений, фактов и общих положений по определенным правилам вывода.

Основные понятия логики.
Примеры:
Параллелограмм – это 4-х угольник, у которого противоположные стороны параллельны.
В параллелограмме противоположные углы равны.
Если в 4-х угольнике две стороны параллельны и равны, то этот 4-х угольник – параллелограмм.
Назовите к каким формам мышления относится каждое предложение. В умозаключении назовите условие и заключение. Приведите свои примеры понятия, суждения, умозаключения.

Основные понятия логики.
Но не всякое предложение является высказыванием. Например предложения «ученик десятого класса» и «информатика - интересный предмет» не являются высказываниями.
Первое предложение ничего не утверждает об ученике.
Второе использует слишком неопределенное понятие «интересный предмет».

Основные понятия логики.
Высказываниями не являются:
1. Предложения, содержащие переменные,
так как нам не известно, какое значение принимает переменная и, соответственно, неизвестно будет истинным это предложение или ложным.
2. Восклицательные и вопросительные предложения,
это не повествовательные предложения.
3. Определения.
мы не можем судить о том истинно такое предложение или ложно, ведь определение – это мы что-то так назвали и расшифровали, что это такое. Кто-то может сказать, что это не так и придумать своё определение.

Основные понятия логики.
Предложения типа «в городе А более миллиона жителей», «у него голубые глаза» не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения, о каком конкретно городе или человеке идет речь.
Такие предложения называются высказывательными формами .
Высказывательная форма - это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Основные понятия логики.
Рассмотрим примеры:
1. 50 · 4 (не является высказыванием – нельзя сказать 1 или 0)
2. 50 = 42 + 8 (высказывание, 1)
3. Я сижу за компьютером (высказывание, 1)
4. В атаку! (не является высказыванием - восклицательное)
5. 5х – 6 = 9 (не является высказыванием – есть переменная)
6. 9 > 12 (высказывание, 0)
7. х < 43 (не является высказыванием – есть переменная)
8. Здравствуйте (не является высказыванием – нельзя сказать 1 или 0)
9. Две прямые в пространстве называются параллельными, если они лежат на одной плоскости и не пересекаются (не является высказыванием, так как определение)

Задание 1.
Какие из предложений являются суждениями и каково их значение истинности?
а) «Сижу и смотрю»
б) «Верно ли, что π = 3,1415926…?»
в) «математическое доказательство»
г) «z+5=45»
д) «20+30+40+10=100»

Задание 2:
Приведите примеры:
а) истинного и ложного высказываний;
б) предложения, не являющегося высказыванием;
с) высказывательной формы.
(запишите в тетрадь)

Задание 3.
Из представленных суждений получите третье в виде умозаключения:
А = «Сумма цифр трехзначного числа равна 7»
B = «Цифры десятков и единиц одинаковы»

Виды суждений
Частные – выражают конкретные (частные) факты.
Например:
«Луна – спутник Земли»
«7 – 2 > 3»
Общие –
характеризуют свойства группы объектов или явлений.
Например:
«В любом прямоугольном треугольнике есть прямой угол»
«X2 ≥ 0»

Виды суждений
Простое суждение – никакая его часть не является суждением
«Париж – столица России» (простое, ложное)
Сложные суждения –
Образованы из нескольких суждений с помощью определенных способов соединения суждений.
«Если в 4-х угольнике все стороны равны, то этот 4-х угольник является ромбом»

Примеры
Рассмотрим примеры простых и сложных высказываний:
1. На улице хорошая погода (простое)
2. Когда я пойду домой, по дороге куплю хлеб (сложное, состоит из двух простых: «я пойду домой» и «я по дороге куплю хлеб»)
3. Если из двух вычесть пять, то получится восемь (простое: «из двух вычесть пять» и «получится восемь» – сами по себе не являются высказываниями)
4. Если 2+3=5 - истина, то 5=2+3 – тоже истина (сложное: «2+3=5 - истина» и «5=2+3 – тоже истина»).

Задание 4.
Укажите, какие из суждений являются частными, а какие общими, укажите значение истинности для каждого суждения:
а) (x + y) (x – y) = x2 – y2
б) «Любой ромб является параллелограммом»
в) «a3=a2, если a=1»
г) 32 + 22 = 52
д) «Меркурий – спутник Марса»
е) «Джордано Бруно – ученик Галилео Галилея»

Задание 5.
Из сложных суждений выделите простые и обозначьте их буквами:
а) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
б) Есть мера вещей и существуют известные границы (афоризм Горация)
в) Студент запланировал выполнить следующие дела: подготовиться к зачету, побывать на тренировке, почитать книгу.
г) Если завтра будет туман, мы не сможем вылететь на соревнования

Домашнее задание.
§ 3.1
Конспект урока.
Примеры:
а) определения, суждения, умозаключения;
б) предложения, не являющегося суждением;
в) частного и общего суждения;
г) простого и сложного суждения.

Е.А. Тулаева МОУ СОШ №18 г.Пенза
Алгебра
суждений

Повторение
Что такое логика, ее главная задача.
Что такое понятие, суждение, умозаключение, рассуждение?
Какие значения могут принимать суждения?
Какие суждения называют частными и общими?
Что такое простое и сложное высказывание?
Приведите примеры.

Рассмотрим следующие примеры сложных высказываний и связь между простыми высказываниями:
1. Если 12 делится на 6, то делится и на 3 (простые высказывания: «12 делится на 6» и «12 делится на 3»; связь «если, то»).
2. На улице льёт дождь или светит солнце (простые высказывания: «на улице льёт дождь» и «на улице светит солнце»; связь «или»)
3. Дома отключили свет и воду (простые высказывания: «дома отключили свет» и «дома отключили воду»; связь «и»)
4. Два числа равны тогда и только тогда, когда их разность не равна нулю (простые высказывания: «два числа равны» и «разность двух чисел не равна нулю»; связь «тогда и только тогда, когда» и «не»)

Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить сложные высказывания.
Такие слова и словосочетания называются логическими связками.
Иначе они называются ...

Основные логические операции
I. Инверсия.
II. Конъюнкция.
III. Дизъюнкция.
IV. Строгая дизъюнкция.
V. Импликация
VI. Эквивалентность.

ИНВЕРСИЯ
Обозначение: Ā, not A.
Пример:
А - Дождя не будет
Ā - Неверно, что дождя не будет
Таблица истинности
Логическое отрицание
1) НЕ
2) НЕВЕРНО, ЧТО

Задание 2:
Приведите пример высказывания и его отрицания.
Определите истинность каждого.

КОНЪЮНКЦИЯ
Обозначения: &, and, Λ,•.
Пример:
А - Дождя не будет.
В - Небо голубое.
А&В - Дождя не будет и небо голубое.
Таблица истинности:
Логическое умножение
И

Задание 3:
а) Приведите примеры двух высказываний и получите составное высказывание используя логическую связку «И».
б) Определите истинность или ложность каждого из трех высказываний

ДИЗЪЮНКЦИЯ
Обозначения: OR, V, +
Пример:
А - Дождя не будет.
В - Небо голубое.
А V В - Дождя не будет или небо голубое.
Таблица истинности:
Логическое сложение
ИЛИ

Задание 4:
а) Приведите примеры двух высказываний и получите составное высказывание используя связку «ИЛИ».
б) Определите истинность или ложность каждого из трех высказываний.

Порядок выполнения логических операций:
НЕ.
И
ИЛИ
Если есть скобки, то сначала выполняются действия в скобках

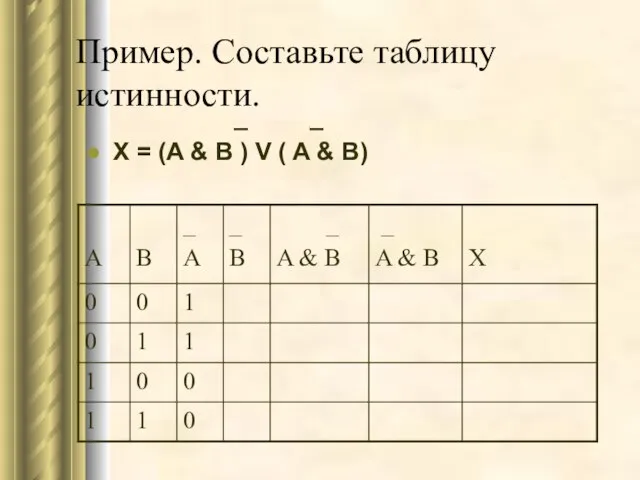
Пример. Составьте таблицу истинности.
_ _
X = (A & B ) V ( A & B)

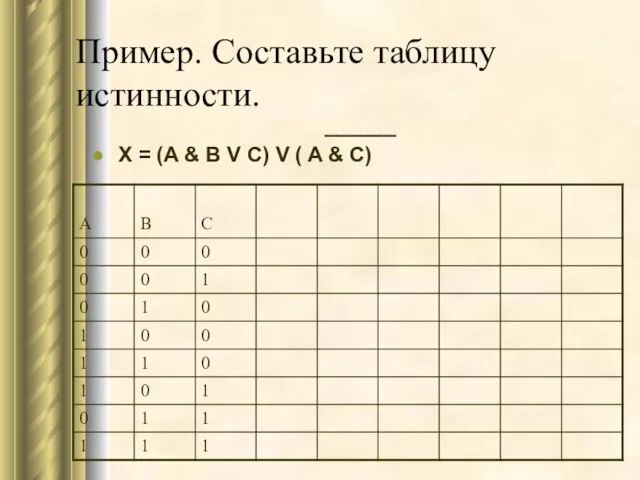
Пример. Составьте таблицу истинности.
______
X = (A & B V C) V ( A & C)

Самостоятельно.
Составьте свое выражение, состоящее из 2 или 3 высказываний, с использованием всех рассмотренных логических операций.

Итог:
Вы познакомились с основными понятиями алгебры логики.
Рассмотрели элементарные логические операции.
Разобрали для каждой логической операции таблицу истинности.

Домашнее задание
§ 3.2
№ 3.1.

Алгебра
суждений
Продолжение (2 урок)

СТРОГАЯ ДИЗЪЮНКЦИЯ
Обозначения: XOR
Пример:
А - Дождя не будет.
В - Небо голубое.
А xor В - Либо дождя не будет, либо небо голубое.
Таблица истинности:
ЛИБО, ЛИБО

Задание 5:
а) Приведите примеры двух высказываний и получите составное высказывание используя связку «ЛИБО, ЛИБО».
б) Определите истинность или ложность каждого из трех высказываний

ИМПЛИКАЦИЯ
Обозначения: →
Пример:
А - Дождя не будет.
В - Небо голубое.
А → В - Если дождя не будет, то небо голубое.
Таблица истинности:
Условная связь
ЕСЛИ, ТО

Задание 6:
а) Приведите примеры двух высказываний и получите составное высказывание используя связку «ЕСЛИ, ТО...».
б) Определите истинность или ложность каждого из трех высказываний

ЭКВИВАЛЕНТНОСТЬ
Обозначения: ↔
Пример:
А - Дождя не будет.
В - Небо голубое.
А↔В - Дождя не будет тогда и только тогда, когда небо голубое.
Таблица истинности:
1) Если и только если
2) Тогда и только тогда, когда